Seam Carving
Implement a content-aware image resizing algorithm.1
Learning goals
Solve a real-world graph problem via reduction.
Reduction is an important tool in computer science theory, but it also has practical applications for solving real-world problems. One of the building blocks of computer science is the idea of abstraction, and reductions represent one of the strongest forms of abstractions by using the solution to one problem as a “black box” for solving a different but somehow related problem.
Represent problem solutions as states in a graph.
In class, we presented several graph algorithms for solving a variety of classical graph problems including shortest paths and minimum spanning trees. But in the real-world, problems rarely immediately jump out as solvable with graph algorithms. How we represent the problem as a graph is one of the most important decisions as it determines which algorithms we can employ to solve the problem.
Apply graph augmentation as a strategy for solving a new class of graph problems.
After coming up with a graph representation of the problem (an abstraction), we can then formally define the problem in terms of the abstraction. However, our problem still might be hard to solve! In seam carving, we need to find the weighted shortest path from any vertex in a distinguished set S to another set T. One common strategy for solving these problems is by augmenting the graph with additional nodes or edges.
Table of contents
Getting Started
Pull the skeleton repository to get the seamcarving assignment. After you update the skeleton code, right-click on the data/ folder, and find the Pull option in the Git > Repository drilldown.
Seam Carver
Seam-carving is a content-aware image resizing technique where the image is reduced in size by one pixel of height (or width) at a time. A vertical seam in an image is a path of pixels connected from the top to the bottom with one pixel in each row; a horizontal seam is a path of pixels connected from the left to the right with one pixel in each column. Below left is the original 505-by-287 pixel image; below right is the result after removing 150 vertical seams, resulting in a 30% narrower image. Unlike standard content-agnostic resizing techniques (such as cropping and scaling), seam carving preserves the most interest features (aspect ratio, set of objects present, etc.) of the image.
Although the underlying algorithm is simple and elegant, it was not discovered until 2007. Now, it is now a core feature in Adobe Photoshop and other computer graphics applications.


In this assignment, you will create a data type that resizes a \(W\)-by-\(H\) image using the seam-carving technique. Finding and removing a seam involves three parts and a tiny bit of notation.
Notation. In image processing, pixel \((x, y)\) refers to the pixel in column x and row y, with pixel \((0, 0)\) at the upper-left corner and pixel \((W - 1, H - 1)\) at the lower-right corner. This is consistent with the Picture data type that we use in this course.
A 3-by-4 image.
| \((0, 0)\) | \((1, 0)\) | \((2, 0)\) |
| \((0, 1)\) | \((1, 1)\) | \((2, 1)\) |
| \((0, 2)\) | \((1, 2)\) | \((2, 2)\) |
| \((0, 3)\) | \((1, 3)\) | \((2, 3)\) |
- Warning
- This is the opposite of the standard mathematical notation used in linear algebra, where \((i, j)\) refers to row \(i\) and column \(j\) and \((0, 0)\) is at the lower-left corner.
We also assume that the color of each pixel is represented in RGB space, using three integers between 0 and 255. This is consistent with the Color data type.
Energy calculation. The first step is to calculate the energy of a pixel, which is a measure of its importance—the higher the energy, the less likely that the pixel will be included as part of a seam (as you will see in the next step). In this assignment, you will use the dual-gradient energy function, which is described below. Here is the dual-gradient energy function of the surfing image above:
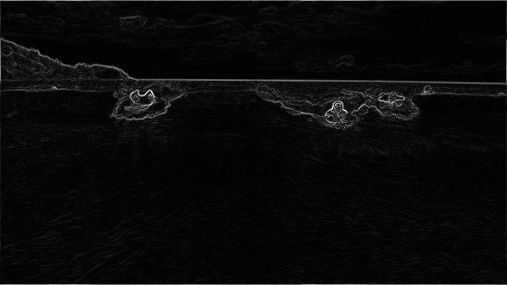
The energy is high (white) for pixels in the image where there is a rapid color gradient (such as the boundary between the sea and sky and the boundary between the surfing Josh Hug on the left and the ocean behind him). The seam-carving technique avoids removing such high-energy pixels.
Implement
SeamCarver.energy.Seam identification. The next step is to find a vertical seam of minimum total energy. (Finding a horizontal seam is analogous.) This is similar to the classic shortest path problem in an edge-weighted digraph, but there are three important differences:
- Each edge weight is based on a vertex (pixel) rather than the edge itself.
- The goal is to find the shortest path from any of the \(W\) pixels in the top row to any of the \(W\) pixels in the bottom row.
- The digraph is acyclic, where there is a downward edge from pixel \((x, y)\) to pixels \((x - 1, y + 1)\), \((x, y + 1)\), and \((x + 1, y + 1)\), assuming that the coordinates are in the prescribed ranges.
Seams cannot wrap around the image (e.g., a vertical seam cannot cross from the leftmost column of the image to the rightmost column).
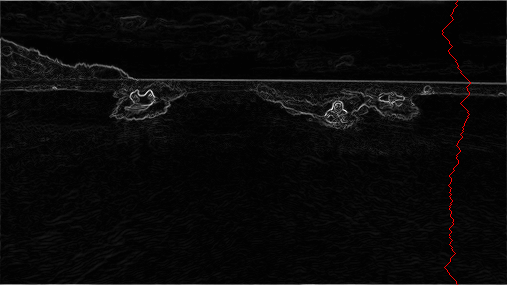
Implement
AStarSeamCarver.findHorizontalSeamandAStarSeamCarver.findVerticalSeam.Seam removal. The final step is remove from the image all of the pixels along the vertical or horizontal seam. This has already been implemented for you as default methods from the
SeamCarverinterface.
Dual-Gradient Energy Function
\(\mathrm{energy}(x, y) = \sqrt{\nabla_x^2(x, y) + \nabla_y^2(x, y)}\)
where the square of the x-gradient \(\nabla_x^2(x, y) = R_x(x, y)^2 + G_x(x, y)^2 + B_x(x, y)^2\), and where the central differences \(R_x(x, y)\), \(G_x(x, y)\), and \(B_x(x, y)\) are the absolute value in differences of red, green, and blue components between pixel \((x + 1, y)\) and pixel \((x - 1, y)\). The square of the y-gradient \(\nabla_y^2(x, y)\) is defined in an analogous manner. To handle pixels on the borders of the image, calculate energy by defining the leftmost and rightmost columns as adjacent and the topmost and bottommost rows as adjacent. For example, to compute the energy of a pixel \((0, y)\) in the leftmost column, use its right neighbor \((1, y)\) and its “left” neighbor \((W - 1, y)\).
As an example, consider the 3-by-4 image with RGB values (each component is an integer between 0 and 255) as shown in the table below. (This is the 3x4.png image in your data/images folder.)

Example 1
The energy of the non-border pixel \((1, 2)\) is calculated from pixels \((0, 2)\) and \((2, 2)\) for the x-gradient
\(R_x(1, 2) = 255 - 255 = 0\)
\(G_x(1, 2) = 205 - 203 = 2\)
\(B_x(1, 2) = 255 - 51 = 204\)
yielding \(\nabla_x^2(1, 2) = 2^2 + 204^2 = 41620\);
and pixels \((1, 1)\) and \((1, 3)\) for the y-gradient
\(R_y(1, 2) = 255 - 255 = 0\)
\(G_y(1, 2) = 255 - 153 = 102\)
\(B_y(1, 2) = 153 - 153 = 0\)
yielding \(\nabla_y^2(1, 2) = 102^2 = 10404\).
Thus, the energy of pixel \((1, 2)\) is \(\sqrt{41620 + 10404} = \sqrt{52024}\).
What is the energy of pixel (1, 1)?
The energy of pixel \((1, 1)\) is \(\sqrt{204^2 + 103^2} = \sqrt{52225}\).
Example 2
The energy of the border pixel \((1, 0)\) is calculated by using pixels \((0, 0)\) and \((2, 0)\) for the x-gradient
\(R_x(1, 0) = 255 - 255 = 0\)
\(G_x(1, 0) = 101 - 101 = 0\)
\(B_x(1, 0) = 255 - 51 = 204\)
yielding \(\nabla_x^2(1, 0) = 204^2 = 41616\).
Since there is no pixel \((x, y - 1)\) we wrap around and use the corresponding pixel from the bottom row the image, thus performing calculations based on pixel \((x, y + 1)\) and pixel \((x, H - 1)\).
\(R_y(1, 0) = 255 - 255 = 0\)
\(G_y(1, 0) = 255 - 153 = 102\)
\(B_y(1, 0) = 153 - 153 = 0\)
yielding \(\nabla_y^2(1, 0) = 102^2 = 10404\).
Thus, the energy of pixel \((1, 0)\) is \(\sqrt{41616 + 10404} = \sqrt{52020}\).
Summary
The energy for each pixel is given in the table below.
| \(\sqrt{20808}\) | \(\sqrt{52020}\) | \(\sqrt{20808}\) |
| \(\sqrt{20808}\) | \(\sqrt{52225}\) | \(\sqrt{21220}\) |
| \(\sqrt{20809}\) | \(\sqrt{52024}\) | \(\sqrt{20809}\) |
| \(\sqrt{20808}\) | \(\sqrt{52225}\) | \(\sqrt{21220}\) |
Finding a Vertical Seam
The findVerticalSeam method returns an array of length \(H\) such that entry \(y\) is the column number of the pixel to be removed from row \(y\) of the image. Consider the 6-by-5 image (6x5.png) with RGB values shown in the table below.
| (78, 209, 79) | (63, 118, 247) | (92, 175, 95) | (243, 73, 183) | (210, 109, 104) | (252, 101, 119) |
| (224, 191, 182) | (108, 89, 82) | (80, 196, 230) | (112, 156, 180) | (176, 178, 120) | (142, 151, 142) |
| (117, 189, 149) | (171, 231, 153) | (149, 164, 168) | (107, 119, 71) | (120, 105, 138) | (163, 174, 196) |
| (163, 222, 132) | (187, 117, 183) | (92, 145, 69) | (158, 143, 79) | (220, 75, 222) | (189, 73, 214) |
| (211, 120, 173) | (188, 218, 244) | (214, 103, 68) | (163, 166, 246) | (79, 125, 246) | (211, 201, 98) |
The minimum energy vertical seam is highlighted in blue. In this case, the method findVerticalSeam returns the array [3, 4, 3, 2, 2] because the pixels in the minimum energy vertical seam are \((3, 0), (4, 1), (3, 2), (2, 3), (2, 4)\).
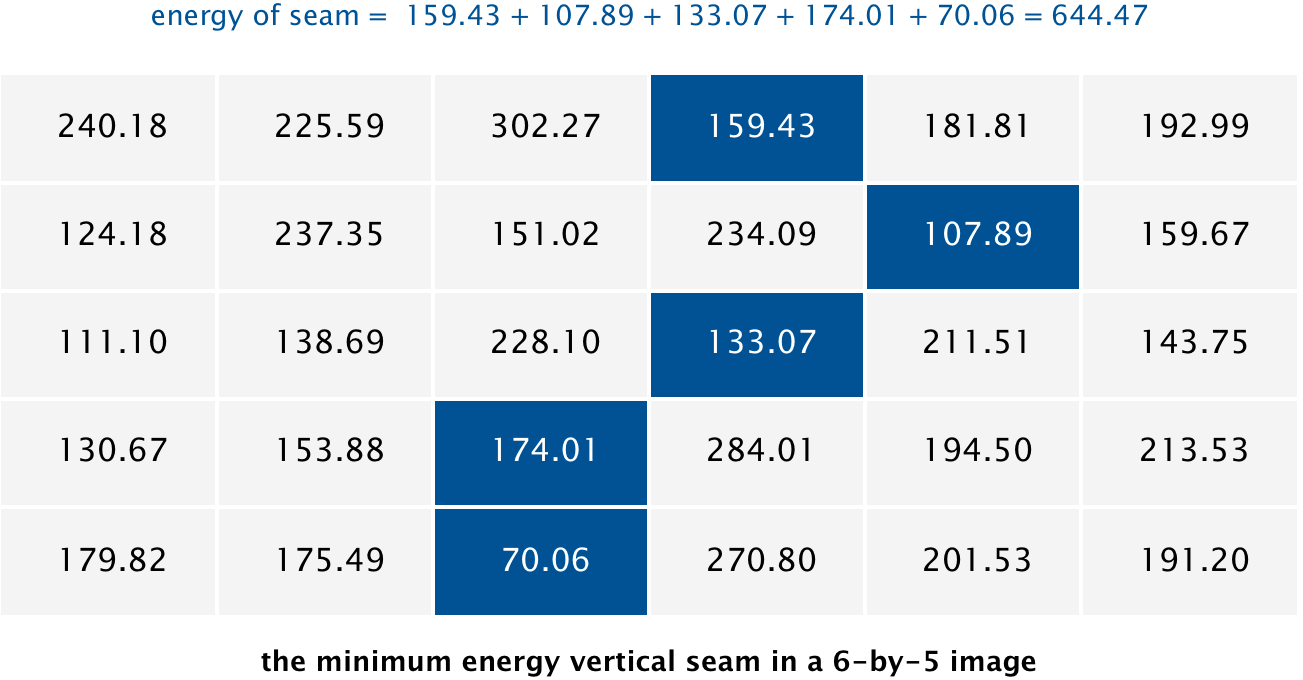
When there are multiple vertical seams with minimal total energy, your method can return any such seam.
Finding a Horizontal Seam
The behavior of findHorizontalSeam is analogous to that of findVerticalSeam except that it should return an array of length \(W\) such that entry \(x\) is the row number of the pixel to be removed from column \(x\) of the image. For the 6-by-5 image, the method findHorizontalSeam returns the array [2, 2, 1, 2, 1, 2] because the pixels in the minimum energy horizontal seam are \((0, 2), (1, 2), (2, 1), (3, 2), (4, 1), (5, 2)\).
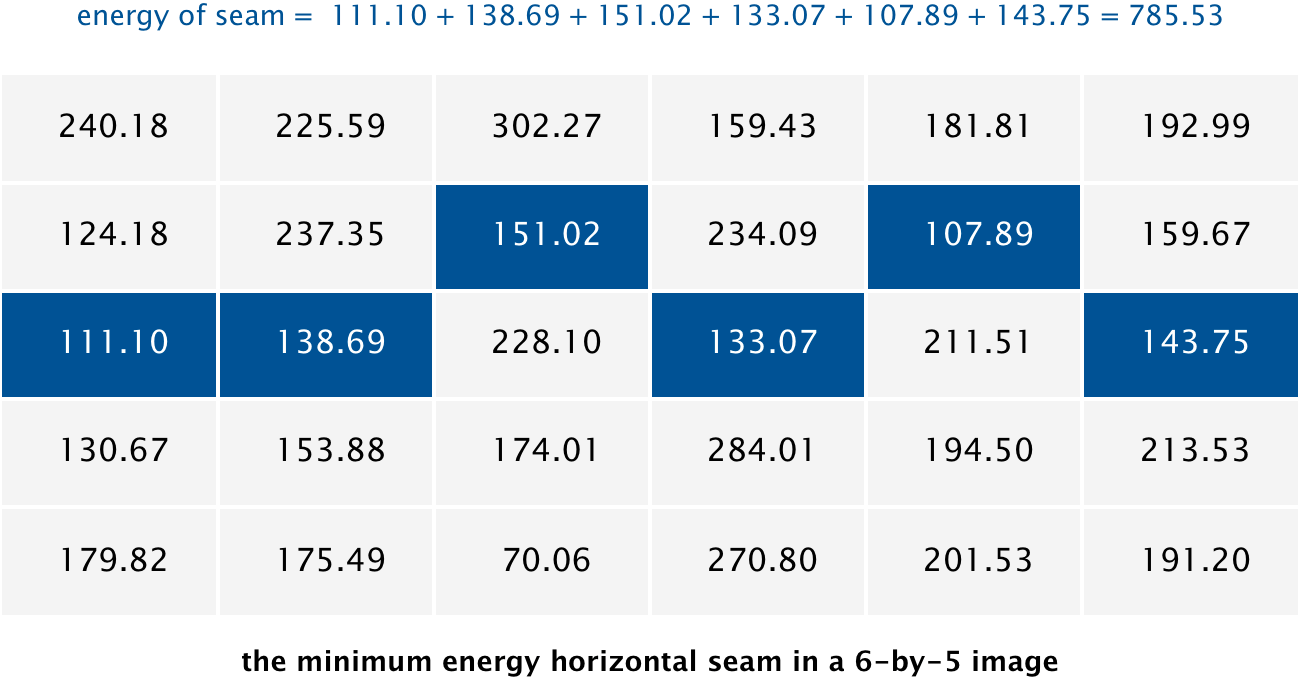
Program Requirements
The runtime of energy is in \(\Theta(1)\) because it is a closed-form expression. The runtime for finding either the vertical seam or the horizontal seam are both in \(O(WH \log (WH))\).
By convention, the indices x and y are integers between \([0, W - 1]\) and between \([0, H - 1]\) respectively. Throw an IndexOutOfBoundsException if either x or y is outside its prescribed range.
Tips
The solver needs a graph to run on, so you’ll need to implement an AStarGraph for this reduction.
- Vertices represent pixels.
- Edges exist from a pixel to its 3 downward neighbors.
- Edges have weight representing energy.
- The shortest (least total weight) path from top to bottom represents the minimum-energy seam.
Look at the example graph implementations from the A* search assignment. Notice that the graphs for puzzles don’t actually store a complete representation of the graph. They instead generate the output for neighbors when the method gets called. This reduces the overall memory usage and runtime for large graphs.
For the heuristic estimatedDistanceToGoal, it’s fine to just always return 0.
Optional Extension: Optimizing Runtime
Design two new classes that implement the SeamCarver interface using the following asymptotically-faster algorithms.
- DAG shortest paths algorithm.
- Dynamic programming, which is similar to the DAG shortest paths algorithm but doesn’t require an explicit graph representation.
Furthermore, we often want to remove multiple seams from an image. A natural approach is to use a greedy algorithm: compute the shortest paths and then remove as many seams as necessary from this initial computation. Can you improve on this algorithm?
Submission
Commit and push your changes to GitLab before submitting your homework to Gradescope.
Josh Hug. 2015. Seam Carving. In Nifty Assignments 2015. http://nifty.stanford.edu/2015/hug-seam-carving/
Josh Hug, Kevin Wayne, and Maia Ginsburg. 2019. Seam Carving. In COS 226, Spring 2019. https://www.cs.princeton.edu/courses/archive/spring19/cos226/assignments/seam/specification.php ↩