Contraction Hierarchies
Parallelizing real-world algorithms with graph theory.1
Learning Goals
Identify synchronization and concurrency issues in real-world algorithms.
Not all algorithms can be parallelized efficiently. Shared mutable memory requires synchronized access and locks to ensure there are no race conditions. In order to avoid race conditions but still write efficient programs, we often need to use different data structures and algorithms to reduce sharing mutable memory.
Apply Java streams and functional interfaces to implement parallel algorithms.
Divide-and-conquer recursive algorithms represent one model for parallel computation. An approach better supported by Java libraries is based on iterating over sequences via stream processing. The specific computations needed to implement a multi-pass parallel algorithm can be broken down into component functions that are then passed to the stream library to compute in parallel.
Table of contents
Getting Started
Pull the skeleton repository to update the huskymaps package, which should now contain four new classes: ContractedNode, ContractedShortestPaths, ContractedStreetMapGraph, and WeightedShortcut.
Contraction Hierarchies
For the single-pair shortest paths problem, the fewer nodes that an algorithm explores, the better the runtime. Dijkstra’s algorithm and A* search solve single-pair shortest paths problems by iteratively relaxing the next closest unvisited vertex until reaching the target vertex. For an 80-mile route search query, Dijkstra’s algorithm could explore about 500,000 nodes while A* search improves by exploring 50,000 nodes.
Contraction hierarchies solve the same 80-mile query by exploring only about 600 nodes. This translates to solving the problem in under 100ms as opposed to over 1.5 seconds or longer. Contraction hierarchies is a two-stage algorithm that improves upon Dijkstra’s algorithm by skipping unimportant nodes during the search query.
Contraction hierarchies apply the idea of node contraction to speedup single-pair shortest path queries on road network graphs. Ignoring traffic conditions, consider the following vague navigation directions between Seattle-Tacoma International Airport and the University of Washington (UW).
- Drive on local roads to the nearest northbound highway onramp towards UW.
- Continue driving northbound on the highway towards UW until arriving at the nearest exit.
- Exit from the highway at the nearest exit and drive on local roads towards UW.
The key assumption in many shortest path queries is that once we arrive on a more important roadway (such as a highway or an avenue), it doesn’t typically make sense to explore side roads until we get close to the destination.
- Node contraction and shortcut edges
- Removing a node and inserting shortcut edges to preserve all shortest paths distances between remaining nodes in the graph. Shortcut edges represent paths from less-important roadways to more-important roadways without needing to explore all of the side roads along the way. The most important roadways (edges) are ones which are used by many shortest path solutions.
- Bidirectional Dijkstra’s algorithm
- In an undirected weighted graph, bidirectional search interleaves the exection of two instances of Dijkstra’s algorithm: one from the start node (forward search) and one from the destination node (backward search). On each iteration, one node is either processed in the forward search or the backward search (depending on distance from the start/destination). The shortest path between the start node and the destination node is found when the forward search meets the backward search.
Contraction hierarchies modifies bidirectional Dijkstra’s algorithm so that it only considers nodes in either increasing contraction order (forward search) or decreasing contraction order (backward search). In other words, the algorithm will not explore exit ramps off a highway.
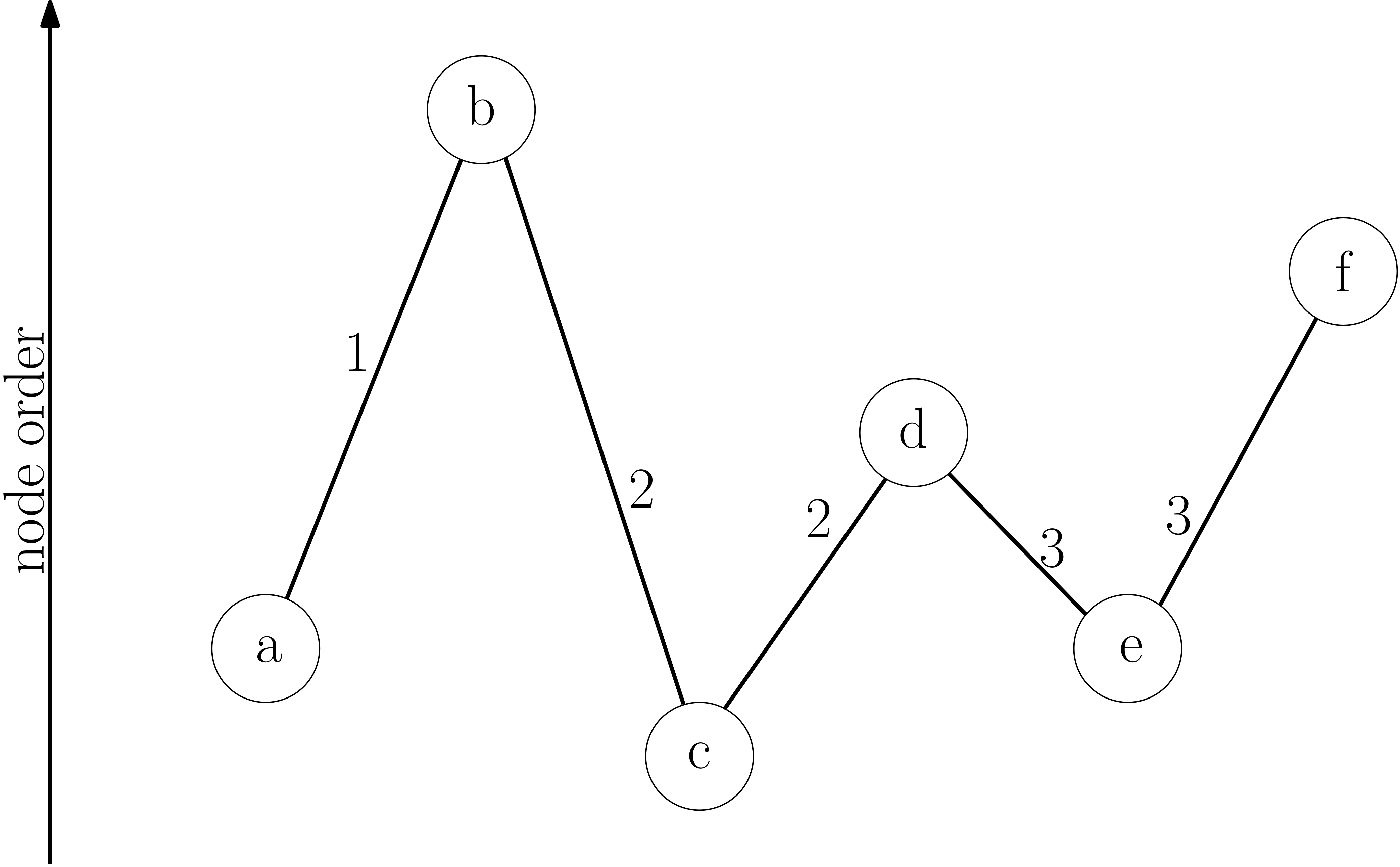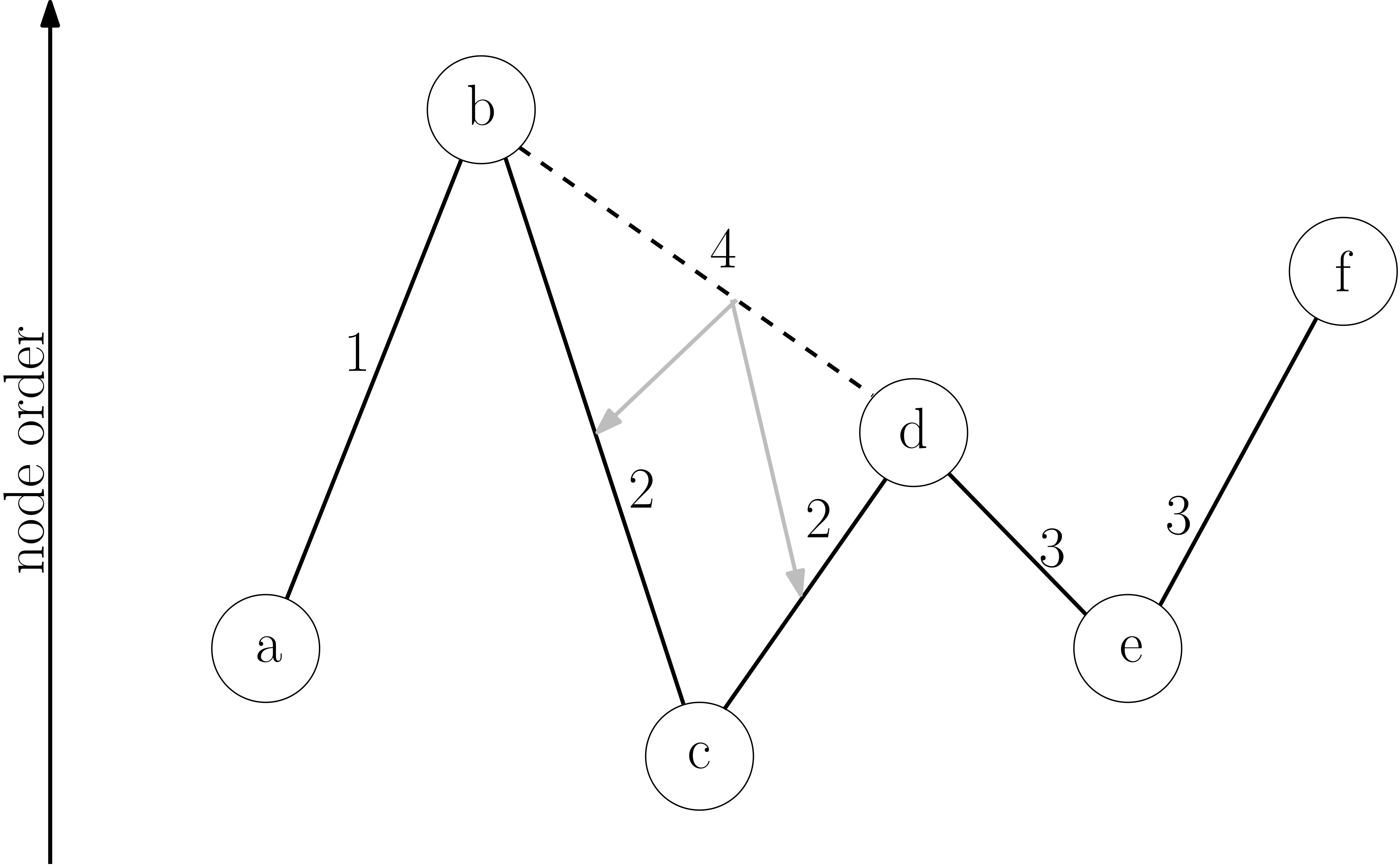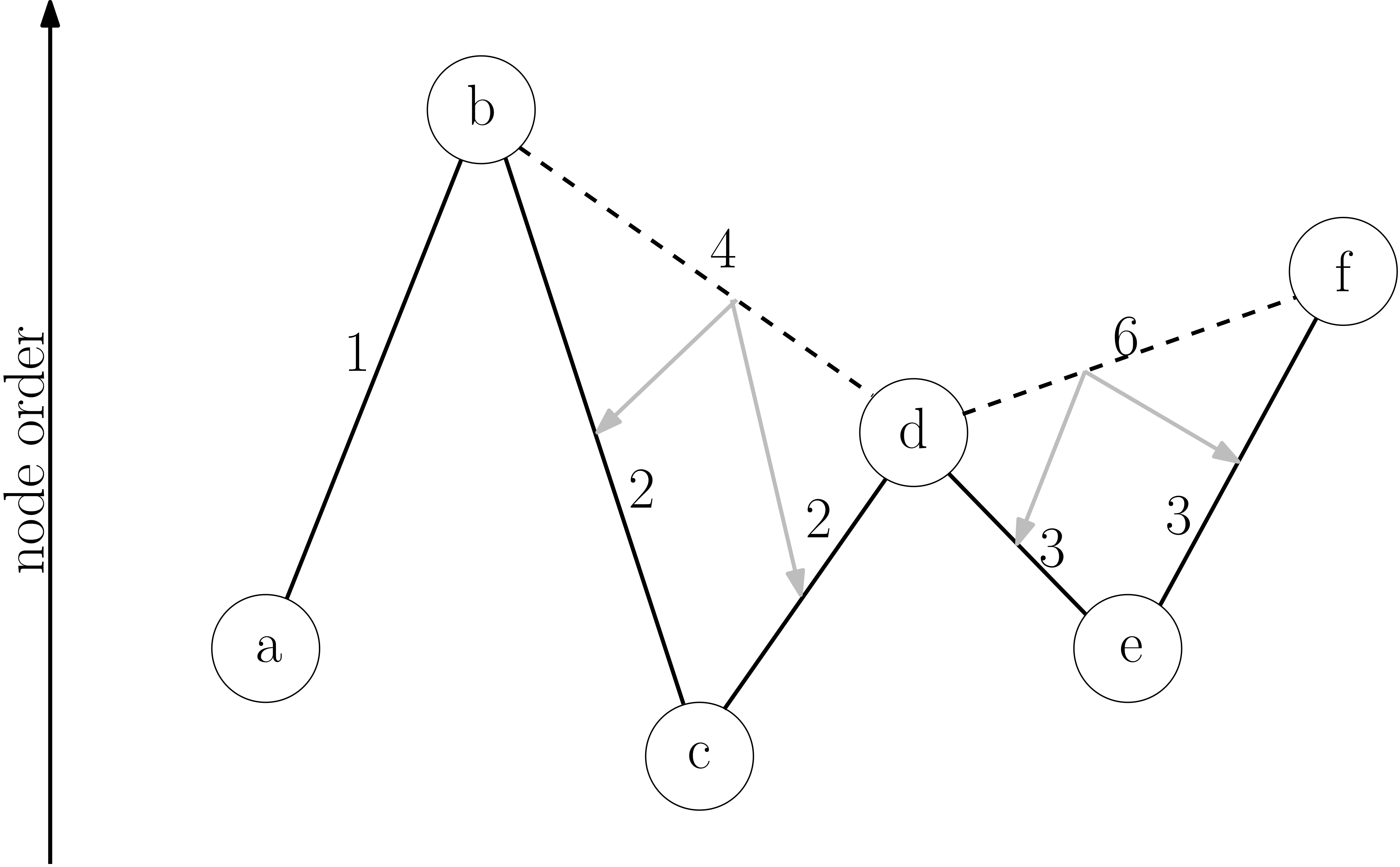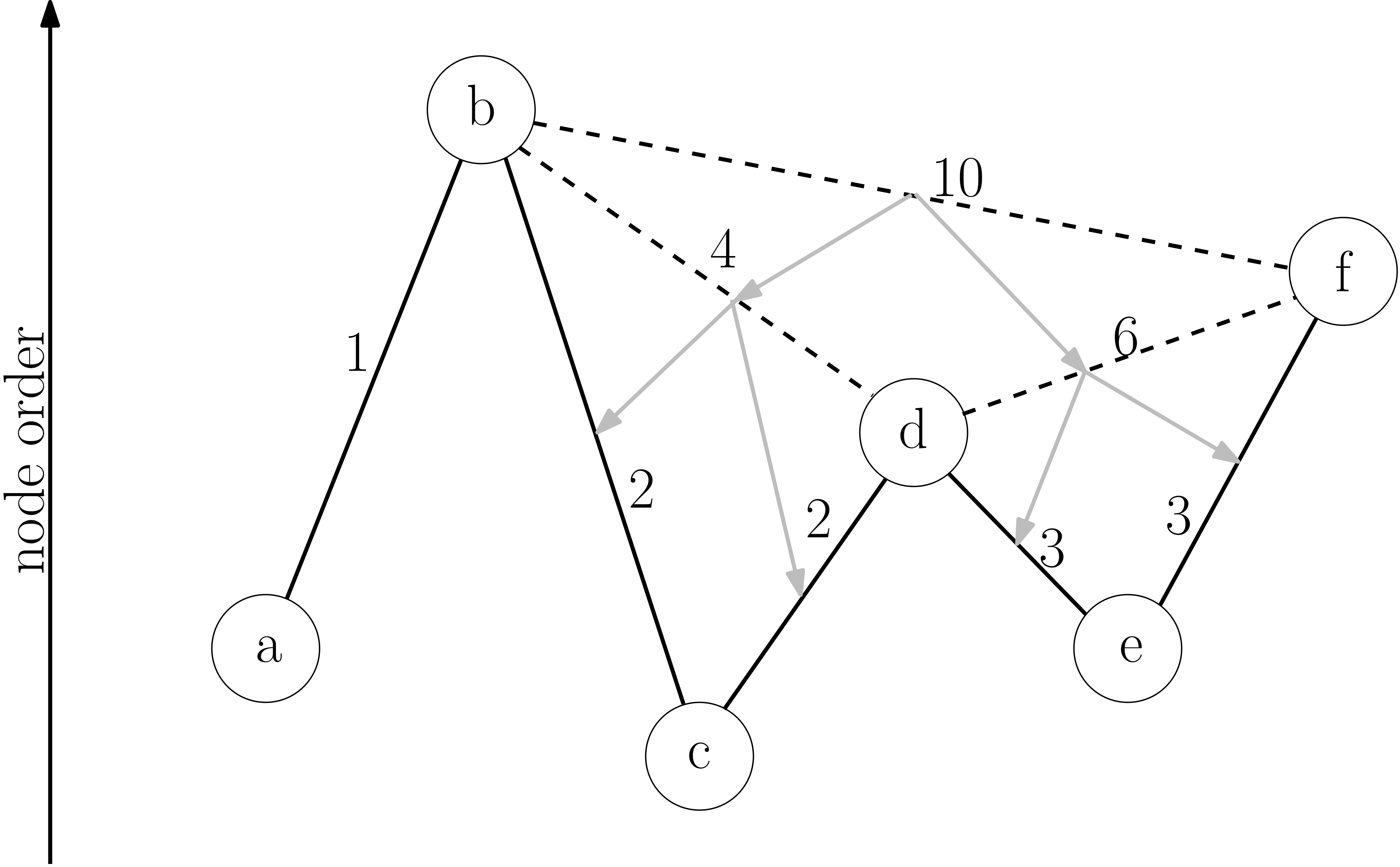
Suppose you start navigation directions while on the highway. How does this algorithm return the shortest route to a local neighborhood?
Although the forward search can’t leave the highway, the backward search starting from the local neighborhood will eventually find the start node on the highway.
The order in which nodes are contracted is crucial to the speed of the route search query: the better the contraction hierarchies model the highway network, the better the runtime. However, updating the heuristic requires a significant amount of computation since the heuristic changes as neighboring nodes are contracted. The goal of this assignment is to speed up graph preprocessing by designing a parallel algorithm for generating contraction hierarchies.
Parallel Contraction Hierarchies
Implement a multi-pass parallel algorithm for generating contraction hierarchies in ContractedStreetMapGraph. While there are still uncontracted nodes:
- In parallel, update the priority for each node.
- In parallel, generate an independent node set.
- In parallel, compute all shortcut edges in the independent node set.
- Contract the independent nodes by inserting the precomputed shortcut edges into the graph.
- Update the uncontracted nodes by removing the independent nodes. (This can be parallelized but there’s not a significant benefit.)
Note that the parallel parts of this algorithm read but never write to the graph. All writes (changes) to the graph occur sequentially so we don’t need to develop a synchronized graph implementation.
- Independent node set
- A set of nodes in the graph where the result of contracting the nodes does not depend on the contraction of any other nodes in the remaining graph. The nodes in an independent node set are far-enough apart such that they can be independently contracted in parallel without introducing data races.
An uncontracted node x is included in the independent node set if it has the maximum priority value among all of its 2-hop nearest neighbors. The isIndependent method provides an implementation of this rule. The priority value is defined by the Priority class, which generates the priority value for a given node. It also stores shortcuts (if they were computed) so that they don’t need to be computed again later.
Shortcuts models (potential) shortcut edges. Each instance of the Shortcuts class contains a list of WeightedShortcut edges. Shortcuts are added to the graph via the addWeightedEdge method. Because the StreetMapGraph is undirected, weighted shortcuts need to be inserted in both directions.
addWeightedEdge(shortcut);
addWeightedEdge(shortcut.flip());
In addition to inserting the shortcut edges, contracting a node also requires two additional method calls.
node.setContractionOrder(order);
node.updateDepths(neighboringNodes(node));
setContractionOrder sets the relative importance of a node. Lower-order nodes represent smaller side streets: these are contracted first. Higher-order nodes represent major roadways: these are contracted last. updateDepths assists the Priority class in determining which nodes to contract next.
After implementing the parallel algorithm, the speedup on seattle.osm.gz improves from a sequential runtime of 446 seconds to 300 seconds with a dual-core, four-thread processor.
Parallel Stream Processing
Divide-and-conquer parallel algorithms, which emphasize a recursive view of parallel programming, are just one model among many others for parallel computation. Another way that we could have implemented parallel SumTask is by using streams. Consider the following sequential code for summing the integers in an input array.
int sum = 0;
for (int x : numbers) {
sum += x;
}
A divide-and-conquer fork/join algorithm would suggest recursively dividing the problem down to a base case defined by the sequential cutoff and then summing the results from each recursive call.
Parallel streams, however, would instead allocate threads to appropriately-sized base cases directly.
int sum = numbers.parallelStream().reduce(0, Integer::sum);
The Java stream library optimizes the code to efficiently parallelize the problem without additional synchronization so long as the methods that we’ve defined don’t require synchronization.
Functional Interfaces
Streams are the most convenient way to parallelize for loops. Suppose we wanted to parallelize the following sequential code for initializing the set of uncontracted nodes.
Set<ContractableNode> uncontractedNodes = new HashSet<>();
for (long id : vertices()) {
ContractableNode node = node(id);
if (isNavigable(node)) {
uncontractedNodes.add();
}
}
A parallelized implementation is provided at the top of the ContractedStreetMapGraph constructor. This code behaves similarly to the above sequential code, though the returned set is unmodifiable. The Java stream library automatically optimizes the code to solve the problem by allocating vertices to multiple threads.
Set<ContractableNode> uncontractedNodes = vertices().parallelStream()
// Map the ContractedStreetMapGraph.node method to each element
.map(this::node)
// Filter each ContractableNode with the StreetMapGraph.isNavigable method
.filter(this::isNavigable)
// Collect the navigable ContractableNode objects into an unmodifiable Set
.collect(Collectors.toUnmodifiableSet());
Most stream method parameters are declared with type Function, Predicate, or Consumer. These classes are part of the Java functional interface.
Function<T, R>- Represents a function that accepts one argument of type
Tand produces a result of typeR. The reference tothis::node, for example, is aFunction<Long, ContractableNode>. Predicate<T>- Represents a function that accepts one argument of type
Tand produces abooleanresult. The reference tothis::isNavigable, for example, is aPredicate<ContractableNode>. Consumer<T>- Represents a function that accepts one argument of type
Tand produces no result.
We can rewrite the parallel code above using lambda expressions to provide more flexibility in defining Java functions. This is useful if you need to pass in additional arguments to functions.
Set<ContractableNode> uncontractedNodes = vertices().parallelStream()
// Map the ContractedStreetMapGraph.node method to each element
.map(id -> this.node(id))
// Filter each ContractableNode with the StreetMapGraph.isNavigable method
.filter(node -> this.isNavigable(node))
// Collect the navigable ContractableNode objects into an unmodifiable Set
.collect(Collectors.toUnmodifiableSet());
Tips
Start by implementing the sequential algorithm and check your work with TestRouterTiny. A working sequential implementation offers a baseline for comparison during implementation of the parallel version.
The parallel algorithm described above does not involve any shared and mutable memory; all memory is either thread-local or shared but immutable (only reads, no writes). Writes only occur sequentially when contracting a node by inserting its shortcut edges into the graph. However, if you need a concurrent data structure for some other reason, avoid data races by using java.util.concurrent implementations such as ConcurrentHashMap.
Optional Extensions
Contraction Ordering Heuristic
The decision problem for the optimal contraction ordering that minimizes preprocessing time is NP-complete.2
To approximate the optimal solution, the Priority class defines a heuristic on the contraction order for nodes in the graph. However, the starter code implements a simplified version of the full heuristic: in particular, it does not include the original edges quotient.1
Route Search Queries
The bidirectional shortest paths implementation in ContractedShortestPaths is simplified to appear as similar as possible to traditional Dijkstra’s algorithm. However, further speedup can be attained through a number of techniques.
- Implement stall-on-demand.1
- Stop the shortest paths search once a node has been removed whose distance from the start vertex (from one direction) is greater than the best total path length (in both directions).
- During preprocessing, remove edges to lower-order nodes.
A simpler optimization is to precompute the shortest paths from every vertex after the contraction hierarchies have been generated. This precomputation can be completed in parallel with synchronized data structures.
Submission
Commit and push your changes to GitLab before submitting your homework to Gradescope.
Christian Vetter. 2010. Fast and Exact Mobile Navigation with OpenStreetMap Data. http://algo2.iti.kit.edu/download/christian_vetter_thesis.pdf
Robert Geisberger, Peter Sanders, Dominik Schults, and Daniel Delling. 2008. Contraction Hierarchies: Faster and Simpler Hierarchical Routing in Road Networks. http://algo2.iti.kit.edu/schultes/hwy/contract.pdf ↩ ↩2 ↩3
Tobias Columbus. 2009. On the Complexity of Contraction Hierarchies. https://i11www.iti.kit.edu/_media/teaching/theses/studienarbeittobiascolumbus.pdf ↩