Introduction to Algorithms

CSE 421 | Spring 2025

Problem Sets

Click here for a LaTeX template you may use.

• Problem Set 1
• Problem Set 2
• Problem Set 3

Logistics and planning your week

Problem sets are roughly weekly, and will be made available on Wednesday evenings. They are typically due the following Wednesday at 11:59pm with submission on Gradescope.

Do not wait to start working on your problem set

It is very valuable to read and understand what each problem is asking soon after it has been assigned. Unlike other courses, even if you really understand the course material, if you leave things late you inevitably will find yourself stuck. One very big advantage to starting early: Once you understand what a question is asking, your brain is a very effective engine for background processing. You should take as much advantage as possible of your ability to be unconsciously working on the problem before you return to it.

As discussed on the syllabus, there are two classes of problems: Mechanical problems and long-form problems. Think about the long-form problems as you would a design for a programming task you have never seen before. (You wouldn't start your work on that coding at the last minute and you shouldn't do that with these problems.) The mechanical problems will generally help with your understanding so they can be good to get out of the way first.

Late days

You are allowed to take four 24-hour extensions on sets, no questions asked (you may use at most one on each sets). After exhausting your four extensions, all future assignments turned in up to one day late will be graded with a 25% penalty, two days late will be graded with a 50% penalty. Assignments turned in after two days late are given automatic zeroes. Extenuating circumstances can be discussed with Prof. Nirkhe -- no TA for this course can approve additional extensions.

Collaboration and Academic integrity

Re-read the detailed discussion in the syllabus.

Grading

How much detail do I include?

When writing pseudocode, your target audience is a competent programmer who has taken a course like CSE 332 (i.e., the other students in this course) but has only just read the problem that you are solving. Remember that you have probably thought about a problem for at least a few hours by the time you are writing up a solution. Your reader has not -- you have much more intuition than they do.

A good check is to ask "would me from last week understand this solution?" and "would me 6 months from now understand this solution?" If not, you are probably relying too much on the intuition you developed, and you should make that intuition explicit.

Our solution for a problem will always fit on one printed page (in LaTeX). It's ok if your solutions are a little longer (it's generally preferable to include too much detail than too little), but they shouldn't need to be much longer than a page.

What if I'm not sure how to do a problem?

Usually, grades for problems go in approximately this order:

• A correct and efficient algorithm.
• An algorithm that is as efficient as the intended solution, and has the main idea of the problem, but mishandles some edge cases.
• An algorithm that is not quite as efficient as the intended solution, but incorporates some of the algorithm design principles that are relevant (e.g., is not just a brute force solution).
• An algorithm that is fundamentally incorrect or signficiantly less efficient than the intended solution or is just a brute force solution.

When designing rubrics, we generally intend it to be to your benefit to have significant, but incomplete, progress toward a correct solution, than to write an incorrect algorithm and intentionally write an incorrect proof.

It is extremely common for our problems to have more than one reasonable solution! If we tell you to use a particular technique, you must use that technique. But otherwise we accept any correct solution.

Style Guide

Expectations for algorithms

When specifying an algorithm, you have to provide the right amount of detail. I often express that this is similar to how you would right a lab report in a chemistry or physics lab today compared to what you would write in grade school. The level of precision is different because you are writing to a different audience. Identically, the audience to whom you are writing you should assume has a fair experience with algorithms and program- ming. If written correctly, your specification should provide the reader with an exercise in programming (i.e. actually implementing the algorithm in a programming language). You should be focusing on the exercise of designing the algorithm. In general, I suggest you follow these guidelines:

• You are writing for a human audience. Don’t write C code, Java code, Python code, or any code for that matter. Write plain, technical English. Its highly recommended that you use LATEX to write your solutions. The examples provided should give you a good idea of how to weave in the technical statements and English. For example, if you want to set m as the max of an array A of values, don’t write a for loop iterating over A to find the maximizing element. Instead the following technical statement is sufficient.

  

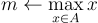
• Don’t spend an inordinate time trying to find ‘off-by-one’ errors in your code. This doesn’t really weigh in much on the design of the algorithm or its correctness and is more an exercise in programming. Notice in the previous example, if written nicely, you won’t even have to deal with indexing! Focus on making sure the algorithm is clear, not the implementation.
• On the other hand, you can’t generalize too much. There should still be a step-by- step feel to the algorithm description. However, there are some simplifications you can make. if we have in class already considered an algorithm X that you want to use as a subroutine to then by all means, make a statement like ‘apply X here’ or ‘modify X by doing (. . . ) and then apply here’. Please don’t spend time writing out an algorithm that is already well known.
• Use prior knowledge, algorithms, theorems, etc. in your proof. A statement like "Ammend DFS to also note ____ per visited vertex" is a great statement in this course. Both you and the graders know exactly what this means and it does not reinvent the wheel. Build correctness proofs using known properties of algrotihms. For example, "Gale Shapley always produces receiver-pessimal solutions. Therefore, ____" is a great way to argue a property of your algorithm if it uses Gale Shapley as a subroutine.
• If you are using a new data structure, explain how it works. Remember that data structures don’t magically whisk away complexity. For example a min heap is O(1) time to find the minimum, but O(log n) time to add an element. Don’t forget these when you create your own data structures. However, if you are using a common data structure like a stack, you can take these complexities as given without proof. Make a statement like ‘Let S be a stack’ and say nothing more.
• When analyzing the running time, unless otherwise noted, you will give the running time in big-O terms. You may need to introduce variable names if they are not given in the problem. A 2-3 sentence justification is usually sufficient (often by giving a quick justification for the running time of the various sections of code).
• When asserting correctness of an algorithm, there are two components. If the algorithm is solving an optimization problem, you have to prove why the output is (a) a feasible solution and (b) why no other output is better. THe latter is usual the hard part. For the decision problem (i.e. binary output of yes/no), you have to argue that the algorithm outputs yes for true instances and no for false instances. By contrapositives, this will prove that it never outputs incorrectly.

Expectations for proofs

In general, proofs in 421 are not graded nearly as strictly as you were used to in 311. In 311, we needed to make sure we know that you know what you're doing. Now that you're in a 400-level course, we believe you know what the starting point of a proof should be, so you'll often be allowed to skip those pieces.

Here are some things we really cared about in 311 that we don't care about in 421

• When doing a direct proof of an implication, you don't need to call this out. properly!
• When doing a proof by induction, you do not need to explicitly define a predicate P()
• If the type of a variable (e.g. "integer" or "character") is clear from context, it does not need to be mentioned when introduced (though it still needs to be mentioned if it appears in the justification of a future step)
• Statements we made you prove in 311 can sometimes be taken as "obvious"
  • For example, the sum of two even numbers being even can just be asserted, it does not need a proof in this class.
  • If in doubt, ask us what we expect to be proven.

On the other hand, some things we do still care about

• Your proof has to be an English proof.
• Non-direct proofs (e.g., proof by contradiction, contrapositive, or induction) need to be introduced as such at the start of the proof.
• In an induction proof, you must say "by IH" (or an equivalent) when using your inductive hypothesis.

Formatting

You are not required to format your solutions using LaTeX but we do insist that solutions be highly legible and well-organized. Solutions that are not will lose points. We do provide a basic LaTeX template for problem sets. We highly recommend use of Overleaf, which is available through UW, for your LaTeX. Remember your output should be expressed in plain, technical English.