Link Search Menu Expand Document
CSE 373

Minimum Spanning Trees

Table of contents

  1. Minimum spanning trees
  2. Prim’s algorithm
  3. Prim’s demo
  4. Kruskal’s algorithm
  5. Kruskal’s demo
  6. MST algorithms
  7. MST vs SPT
  8. Negative edge weights

Minimum spanning trees

Prim’s algorithm

Prim’s demo

Kruskal’s algorithm

Kruskal’s demo

MST algorithms

Consider the following undirected weighted graph.

6 vertex undirected weighted graph

Question 1

Give the order in which Prim’s algorithm selects edges starting from s as a comma-separated list e.g. 1, 2, 3, 4, 5, 6, 7, 8, 9. Not all edges may be needed.

Question 2

After adding the edge with weight 1 to the known set in Prim’s algorithm, which edges are on the cut between the known and unknown vertices?

  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
Explanation

The 4 vertices on the left side of the graph are separated from the 2 vertices on the right edge of the graph. There are 3 edges on the cut between these two sets of vertices.

Question 3

Give the order in which Kruskal’s algorithm selects edges as a comma-separated list e.g. 1, 2, 3, 4, 5, 6, 7, 8, 9. Not all edges may be needed.

Question 4

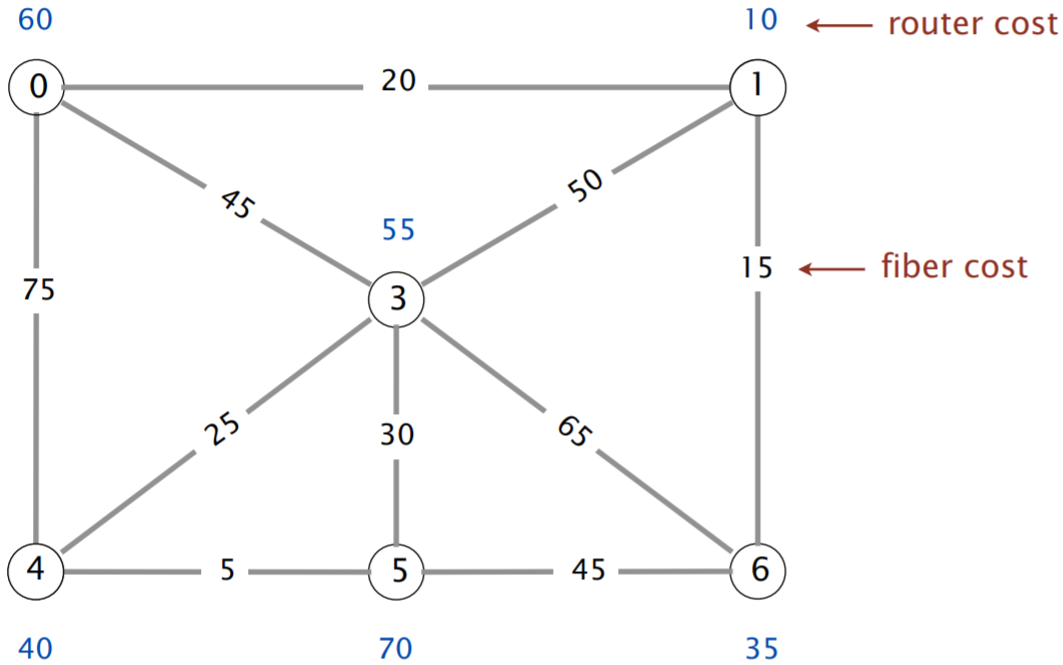
Suppose we want to connect all apartments to the internet. An apartment will receive internet so long as it has either a router installed or a fiber connection. We want to minimize the cost of installation. Give a reduction algorithm to minimum spanning trees for this problem.

Routers and fiber connections

The above example contains 6 apartments and 10 possible fiber connections. The optimal solution installs a router in apartments 1 and 4 (for a cost of 50) and builds fiber connections 0–1, 1–6, 3–4, 4–5 (for a cost of 65).

MST vs SPT

Let’s compare and contrast minimum spanning trees (MSTs) with shortest paths trees (SPTs).

Question 1

Compare and contrast the shortest paths problem and the minimum spanning tree problem.

Question 2

Compare and contrast Prim’s algorithm and Dijkstra’s algorithm.

Negative edge weights

Dijkstra’s algorithm is not guaranteed to return a valid shortest paths tree if the graph contains negative edge weights. How about Prim’s algorithm? Let’s also consider a new strategy for resolving the problem.

Question 1

Consider a graph with negative edge weights. Suppose we added the same constant value to each edge weight such that all of the edges now have non-negative weights.

True/False: If we run Dijkstra’s algorithm on this modified graph, is it guaranteed to return a valid shortest paths tree for the original graph?

Explanation

By increasing each edge weight, we’re inadvertently penalizing paths with more edges! A path from s to t with 2 edges would receive 2 times the constant value to its cost, whereas a direct edge between s and t would only receive a single constant value increase.

Question 2

Consider the same setup as in the prior question.

True/False: If we run Prim’s algorithm on this modified graph, is it guaranteed to return a valid minimum spanning tree for the original graph?

Explanation

This actually does work because Prim’s algorithm does not consider path lengths. Another way to see this is that the cost of any spanning tree is increased by |E| times the constant value, so the minimum spanning tree in the modified graph will be the same as the minimum spanning tree in the original graph.

Question 3

True/False: Prim’s algorithm computes a valid minimum spanning tree in any undirected graph, even ones with negative edge weights.

Explanation

Dijkstra’s algorithm struggled with negative-weight shortcut edges hidden behind otherwise expensive paths. However, since Prim’s algorithm orders the priority queue by lowest-known edge weight rather than lowest-known path cost, these hidden edges will not be a problem. They’ll eventually be added to the minimum spanning tree later if applicable.