Hash Tables

Table of contents

1. Arrays
2. DataIndexedIntegerSet
3. Collisions
4. DataIndexedStringSet
5. Hash tables
6. Separate chaining
7. Hash table analysis
8. Hash table insertion
9. Hash functions
10. LLRB tree buckets

Arrays

Balanced search tree and binary heap data structures guarantee that the height of the tree will be roughly logarithmic with respect to its total size, resulting in tree operations such as search and insertion only taking logarithmic time. This is a massive improvement over linear search. A tree containing over 1 million elements has a height that’s within a constant factor of 20!

How can we do even better than a balanced search tree? Java’s TreeSet and TreeMap classes are represented as red-black trees. In this lesson, we’ll examine hash tables, the data structure behind Java HashSet and HashMap, which can have constant time search and insertion—regardless of whether your hash table contains 1 million, 1 billion, 1 trillion, or even more elements.

Contiguous memory arrays

Arrays are stored contiguously in memory where each array index is next to each other, one after the other. Unlike a linked list, arrays do not need to follow references randomly throughout memory. Indexing into an array is a constant-time operation as a result.

The DataIndexedIntegerSet uses this idea of an array to implement a set of integers. It maintains a boolean[] present of length 2 billion, one index for almost every non-negative integer. The boolean value stored at each index present[x] represents whether or not the integer x is in the set.

void add(int x)

Adds x to the set by assigning present[x] = true.

boolean contains(int x)

Returns the value of present[x].

void remove(int x)

Removes x from the set by assigning present[x] = false.

public class DataIndexedIntegerSet {
    private boolean[] present;

    public DataIndexedIntegerSet() {
        present = new boolean[2000000000];
    }

    public void add(int x) {
        present[x] = true;
    }

    public boolean contains(int x) {
        return present[x];
    }

    public void remove(int x) {
        present[x] = false;
    }
}

While this implementation is simple and fast, it takes a ton of memory to store the 2-billion length present array—and it doesn’t even work with negative integers! Additionally, we’ll also need to come up with a way to generalize this idea so that it works with other data types such as strings.

Let’s focus on the second problem. Say we want to add “cat” to an array-based set of strings. One way to determine where to store “cat” is to use the first character ‘c’ to determine the array index. We can store words with first character ‘a’ at index 1, ‘b’ at index 2, ‘c’ at index 3, etc.

DataIndexedIntegerSet

Collisions

A collision occurs when two or more keys share the same index. One way we can avoid collisions is to be more careful about how we assign each English word. If we make sure every English word has its own unique integer index, then we won’t run into collisions!

Suppose the string “a” goes to 1, “b” goes to 2, “c” goes to 3, …, and “z” goes to 26. Then the string “aa” should go to 27 since (1 ⋅ 26¹) + (1 ⋅ 26⁰) = 27, “ab” to 28, “ac” to 29, and so forth. Since there are 26 lowercase English characters, our base is 26.

Generalizing this pattern, we can compute the index for “cat” as (3 ⋅ 26²) + (1 ⋅ 26¹) + (20 ⋅ 26⁰) = 2074. This mathematical formula is known as a hash function. The result of applying this hash function to the string “cat” is the hash value 2074.

Hash function

Returns an integer representation of a given object called its hash code.

So long as we pick a base that’s at least 26, this hash function is guaranteed to assign each lowercase English word a unique integer. But it doesn’t work with uppercase characters or punctuation. If we want to support other languages than English, we’ll need an even larger base. For example, there are 40,959 characters in the Chinese language alone. A char in Java supports all of these characters and more: to support all strings, the base would need to be 2¹⁶.

To make matters worse, the maximum size of an array in Java is limited to the size of the largest Java int, which is 2,147,483,647. There are more unique strings than there are unique Java int values, so collisions are inevitable!

Question 1

Compute the hash code for “bee” using the hash function above.

DataIndexedStringSet

Hash tables

Separate chaining

Hash tables improve upon data-indexed arrays by handling collisions. We’ll primarily study separate chaining hash tables, though there are other ways of handling collisions.

Separate chaining

A strategy for handling collisions that replaces the boolean[] present with an array of “buckets” where each bucket starts empty. For adding an item x that belongs at index h, add x to bucket h. To avoid duplicates (as required by the set and map ADTs), only add x if it is not already present in the bucket.

Since separate chaining addresses collisions, we can now use smaller arrays. Instead of directly using the hash code as the index into the array, take the modulus of the hash code to compute an index into the array.

Separate chaining comes with a cost. The worst-case runtime for adding, removing, or finding an item is now in Θ(Q) where Q is the size of the largest bucket. Consider how we might implement contains: rather than just returning the true/false boolean value, we’ll need to search through the bucket. The runtime of a separate chaining hash table is affected by the bucket data structure.

contains(Object o)

Compute the hash code of o modulo the length of the array to get the bucket index. Then, search the bucket by calling equals on each item.

Hash table analysis

Hash table insertion

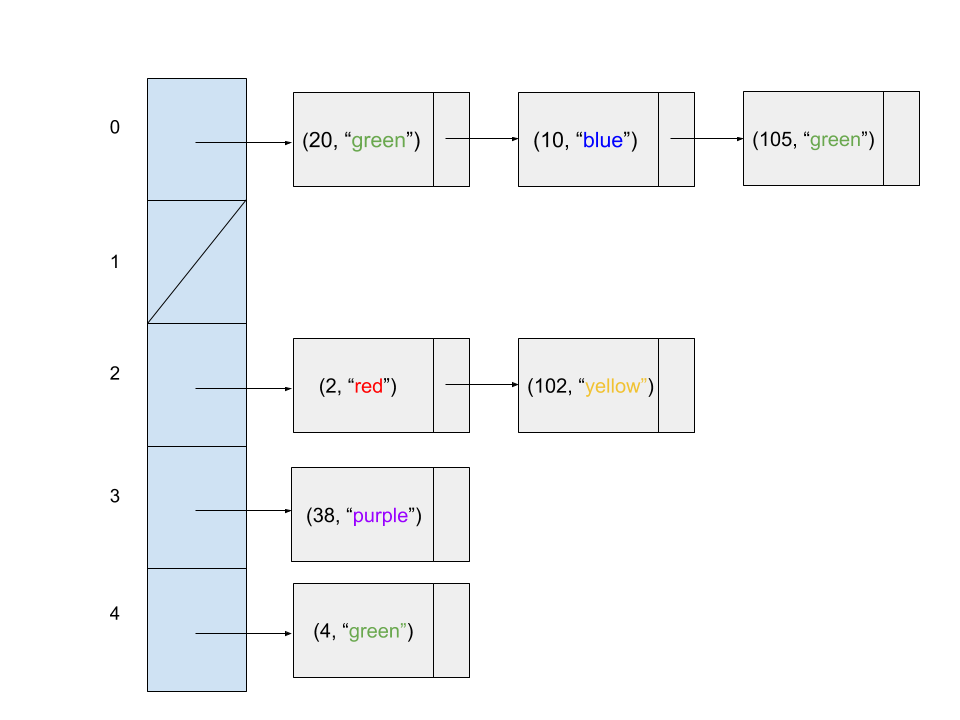
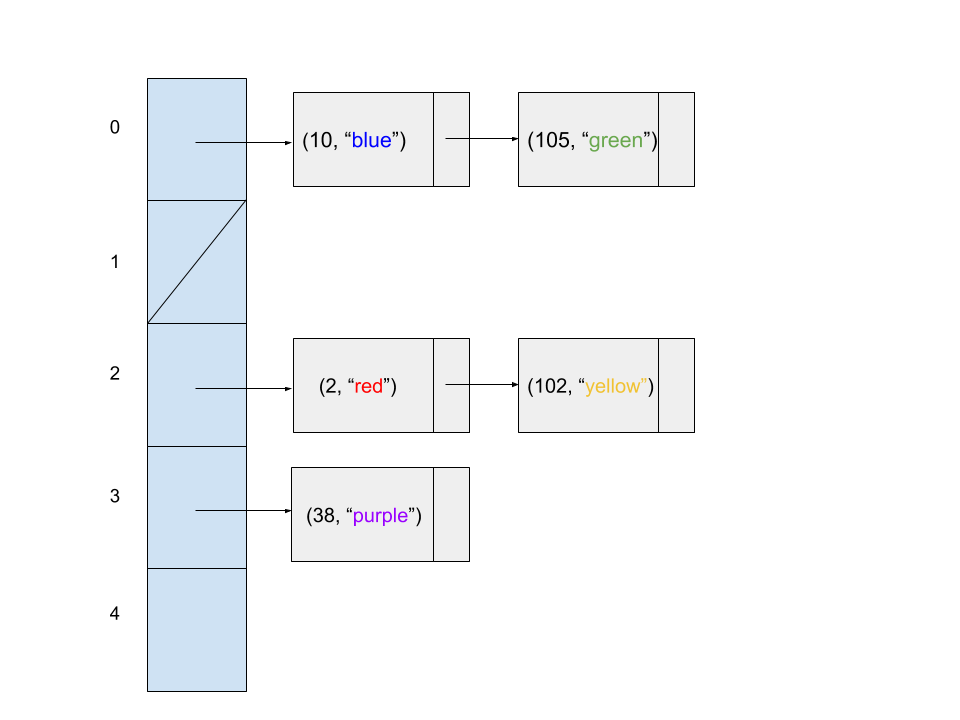
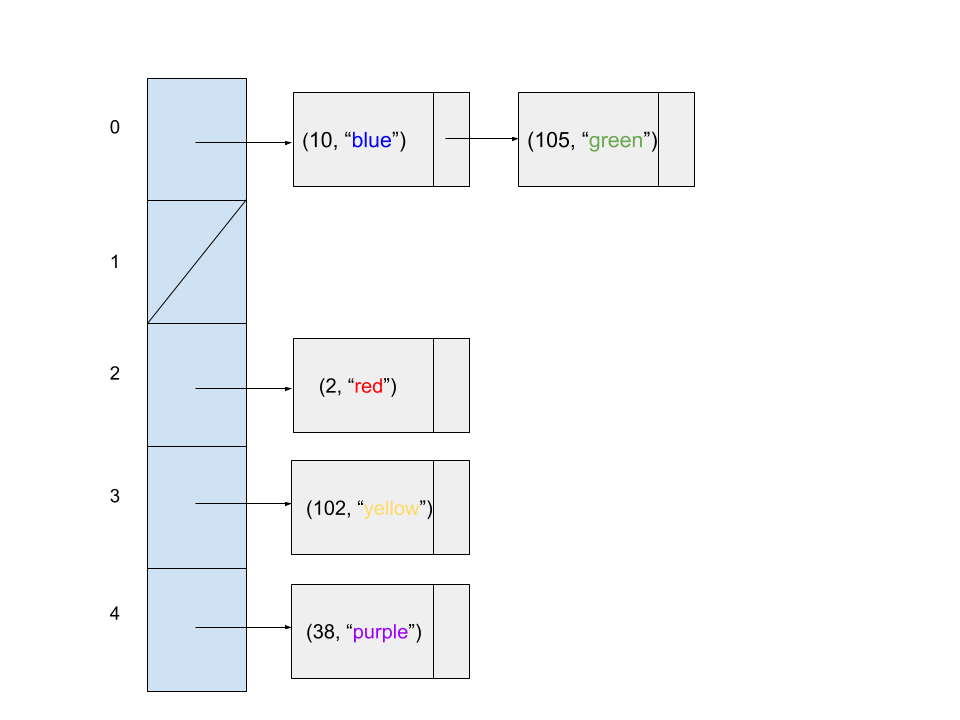
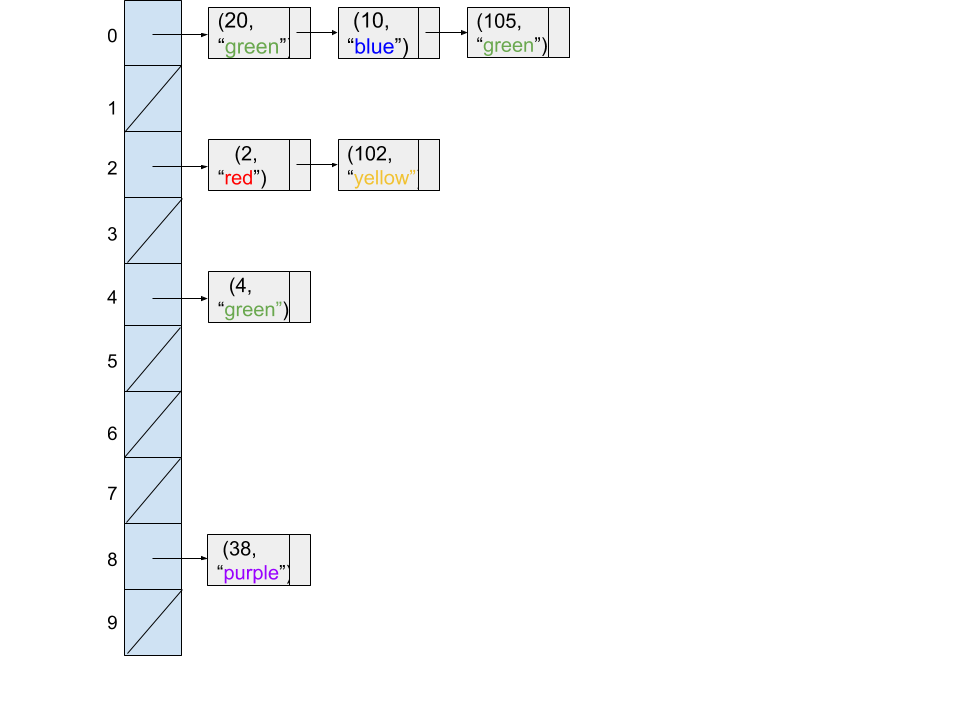
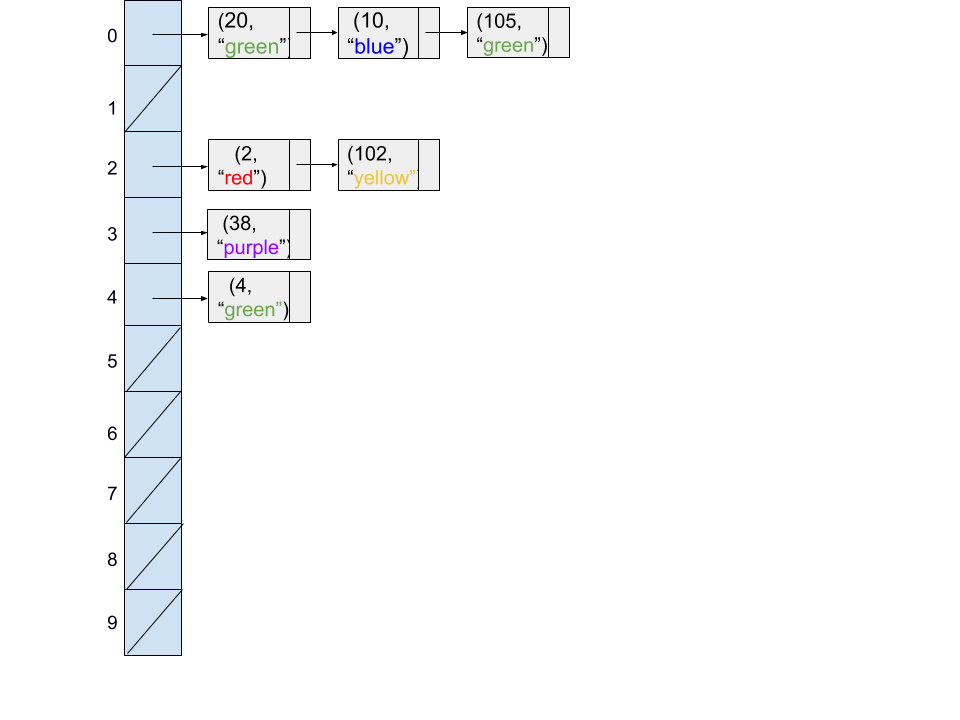
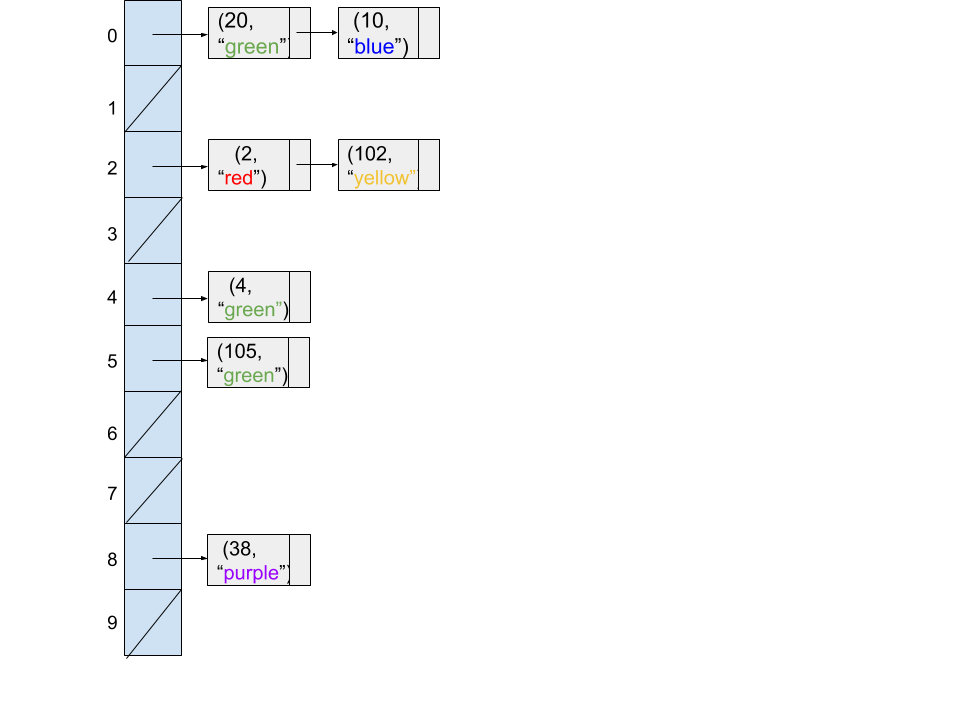
Consider the following code snippet.

Map<Integer, String> map = new HashMap<>();
map.put(20,  "green");
map.put(2,   "red");
map.put(10,  "blue");
map.put(4,   "green");
map.put(105, "green");
map.put(102, "yellow");
map.put(38,  "purple");

Question 1

Assuming the HashMap does not resize and its underlying array is fixed at 5 buckets, which of the following diagrams might represent the state of the hash table at the end of the code snippet?

Question 2

Assuming the HashMap resizes its underlying array when the number of items equals the number of buckets by doubling the number of buckets (from 5 buckets to 10 buckets), which of the following diagrams might represent the state of the hash table at the end of the code snippet?

Hash functions

How does a Java HashSet or HashMap know how to compute each object’s hash code? Unlike search trees that relied on the Comparable interface, Java provides a default hash function implementation. All objects in Java provide a default implementation of the following two methods.

boolean equals(Object o)

Returns true if o is considered equal to this object. The default implementation checks that this == o.

int hashCode()

Returns the hash code for this object. The default implementation returns the memory address for this object.

The Java documentation for Object.hashCode describes the hashCode contract. When overriding the equals method, it is usual necessary to override the hashCode method so that it is consistent with equals.

Question 1

True/false: Suppose we have a Dog class where each Dog has a name and a weight. What must the code output if we want the Dog class to work in a hash table?

Dog d1 = new Dog("Zeus", 5);
Dog d2 = new Dog("Zeus", 5);
// d1.equals(d2) evaluates to true!

System.out.println(d1.hashCode() == d2.hashCode());

Question 2

Suppose the Dog class overrides equals but not hashCode. What could happen if we run the following code?

Dog d1 = new Dog("Zeus", 5);
Dog d2 = new Dog("Zeus", 5);
// d1.equals(d2) evaluates to true!

Set<Dog> dogs = new HashSet<>();
dogs.add(d1);
System.out.println(dogs.contains(d2));

• d1 and d2 will always have the same hashCode.
• d1 and d2 may have the same hashCode.
• d1 and d2 will have only a tiny chance of having the same hashCode.
• The print statement will always print false.
• The print statement will always print true.
• The print statement will sometimes print false and sometimes print true.

Question 3

True/false: Suppose the Dog class overrides hashCode but not equals. Will the following hashCode work in a hash table?

public int hashCode() {
    return 17;
}

Question 4

ArrayList provides valid and effective implementations for equals and hashCode. Why might we still caution storing ArrayList objects in a HashSet, i.e. HashSet<ArrayList<String>>?

• In a hash table, each bucket is a list of items, and you can’t store a list in a list.
• A list can be changed after its creation, so if one of the lists changes, it can get lost in the hash table.
• Lists can be potentially infinitely large but integer hash codes are finite, so collisions are very likely.

LLRB tree buckets

We know that the worst-case runtimes for separate chaining hash table operations are closely related to the size of the largest bucket. In the hash table analysis, we compared hash tables without resizing (fixed number of buckets) versus hash tables with resizing.

Hash tables without resizing

The number of buckets is constant, so the size of the largest bucket is in Θ(N) with respect to N, the total size of the hash table.

Hash tables with resizing

The number of buckets grows linearly with respect to N. Assuming elements are evenly spread across the buckets, then the size of the largest bucket is in Θ(1).

In reality, Java HashSet and HashMap include a special optimization for avoiding worst-case runtime. When a linked list bucket grows contains more than 8 elements, the bucket will be converted into a left-leaning red-black tree. While this optimization does not affect the size of the largest bucket, it might improve the runtime.

For these problems, do not assume elements are evenly spread across the buckets.

Question 1

Consider a hash table without resizing but using LLRB trees as the bucket data structure. Identify the worst-case runtime for inserting an element into this hash table with respect to N, the total size of the hash table.

• Θ(1)
• Θ(log N)
• Θ(N)
• Θ(Nlog N)
• Θ(N²)

Question 2

Consider a hash table with resizing but using LLRB trees as the bucket data structure. Identify the worst-case runtime for inserting an element into this hash table with respect to N, the total size of the hash table.

• Θ(1)
• Θ(log N)
• Θ(N)
• Θ(Nlog N)
• Θ(N²)

Question 2

Consider a hash table with resizing but using LLRB trees as the bucket data structure. Identify the worst-case runtime for inserting an element into this hash table with respect to N, the total size of the hash table.

• Θ(1)
• Θ(log N)
• Θ(N)
• Θ(Nlog N)
• Θ(N²)

Question 3

A team member points out that this idea doesn’t actually help with the worst-case runtime for hash tables with resizing, so we shouldn’t use this idea. Do you agree with their assessment? Why might the Java developers implement this optimization in spite of the absolute worst-case runtime?