Link Search Menu Expand Document
CSE 373

Memory and Caching

Table of contents

  1. How memory looks
  2. How memory is used
  3. B+ trees
  4. Computer components
  5. Locality
  6. B+ tree locality
  7. Suffix arrays

How memory looks

How memory is used

B+ trees

Computer components

For each of the components of a computer below, summarize how that component of the computer might be similar to and how it might differ from RAM (main memory). Compare their function and properties.

Question 1

CPU

Question 2

Disk

Question 3

Cache

Locality

For each of the following code samples, identify whether they are good examples of spatial locality or temporal locality (or neither). Select all that apply and explain your answers.

Question 1

public void sum(int[] arr, int loc, int target) {
    for (int i = 0; i < target; i++) {
        arr[loc] += i;
    }
}
Explanation

This code accesses the same piece of data arr[loc] over and over again.

Question 2

public void addTwo(int[] arr) {
    for (int i = 0; i < arr.length; i++) {
        arr[i]+= 2;
    }
}
Explanation

When an address is accessed from the RAM, it pulls nearby addresses up to the cache. Since arrays are contiguous, you can access those other addresses also from the cache.

Question 3

public class MyLinkedList<T> {
    private Node<T> front;

    public void removeFront(int k) {
        Node<T> curr = this.front;
        Node<T> prev = null;
        for (int i = 0; i < k; i++) {
            prev = curr;
            curr = curr.next;
            prev.next = null;
        }
        this.front = curr;
    }

    private static class Node<T> {
        public final T data;
        public Node<T> next;
   }
}
Explanation

Linked lists are not stored contiguously in RAM. When we access one element from the list, other elements that come after are not accessed and put in the cache. This requires taking many trips to RAM, which take longer than trips to the cache.

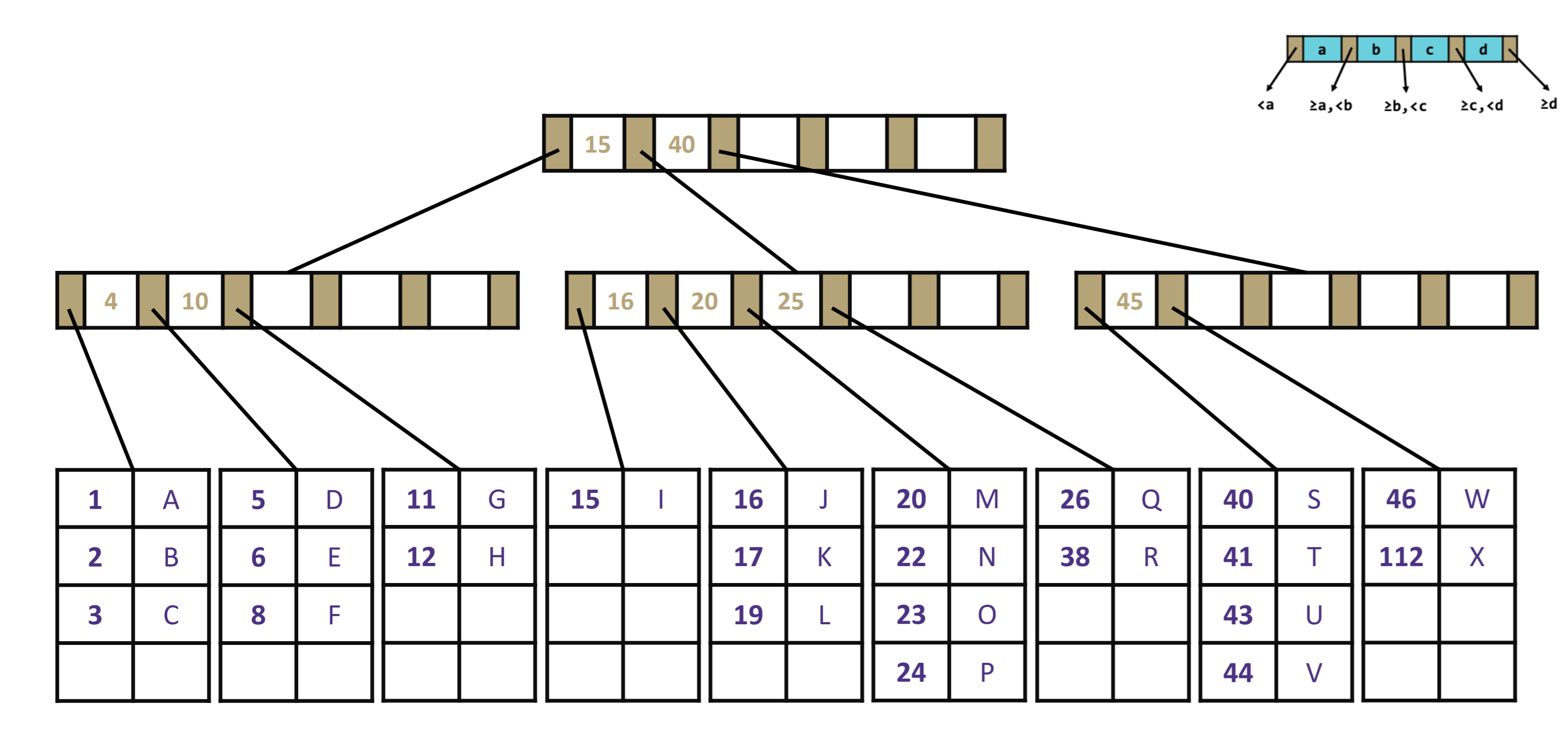
B+ tree locality

For each of the get calls below, describe the nodes that are accessed in order to get the value associated to the given key.

B+ tree

Question 1

get(41)

Question 2

get(25)

Question 3

Which of the following statements are true about B+ trees?

  • Minimizes height so there are fewer nodes to traverse the tree and more nodes at each level.
  • All relevant information about a single node fits in one page.
  • We use as little of the page as we can because it’s slow to access disk.
  • Searching within a node is fast compared to disk access time.
  • Searching within a node is slow.

Suffix arrays

We’ve now seen two ways for more memory-efficiently representing trees as arrays.

  1. Binary heaps are complete trees, so it has a perfect for the array representation.
  2. B+ trees take the idea of 2-3 trees and expand the number of keys per node.

But it turns out that there’s actually another data structure analogy based on concepts we’ve already learned. Remember how we used a ternary search tree to store all of the suffixes of a given DNA sequence? This approach was actually inspired by a real data structure known as a suffix tree!

To improve memory efficiency, algorithm designers turned the suffix tree into the suffix array. The suffix array is the data structure concept behind real-world DNA database systems.