Exhaustive search
Table of contents
Solution space
So far, most of our programming experience has focused on solving problems that have one correct answer associated with each input.
However, we briefly introduced the idea of simulation earlier in the course. The goal of the canWin method is to return true when the player can win, and false is the player is in a losing position. In order to return this boolean, the canWin method simulates all of the possible playthroughs considering the scenarios where each player takes either 1 or 2 cookies from the pile.
public static boolean canWin(int n) {
if (n == 0) {
return false;
} else if (n == 1) {
// Take 1 cookie to win the game
return true;
} else {
// Is the other player forced to lose?
boolean takeOne = !canWin(n - 1);
boolean takeTwo = !canWin(n - 2);
return takeOne || takeTwo;
}
}
In this lesson, we’ll be putting a twist on tree recursion. Rather than determine whether or not the player canWin, our goal is to print out all of the possible playthroughs given two players. This problem involves exploring a solution space that can include many possible answers! Let’s start by considering a smaller example, fourAB, that prints out all strings of length 4 composed only of the letters “a” and “b”.
What are three possible answers to the fourAB problem?
- aaaa
- abba
- babb
- and many others!
Exhaustive search (also known as brute-force search) is a problem-solving technique that works by systematically enumerating all possible answers in a solution space. Instead of arbitrarily guessing all of the possible answers to fourAB, we should instead use a more algorithmic approach.
| aaaa | abaa | baaa | bbaa |
| aaab | abab | baab | bbab |
| aaba | abba | baba | bbba |
| aabb | abbb | babb | bbbb |
What patterns do you notice in the example above?
- The first two columns have answers that only start with an “a”.
- The first column only has answers that start with “aa”.
- The first column, first two entries only has answers that start with “aaa”.
- The very first entry is “aaaa”.
This pattern repeats across the entire table.
By arranging the outputs as such, we can highlight the recursive substructure in the problem.
- The left two columns are associated with prepending an “a” to the start of all of the strings of length 3 composed only of the letters “a” and “b”.
- The right two columns are associated with prepending a “b” to the start of all of the strings of length 3 composed only of the letters “a” and “b”.
Since we’re exhaustively searching the solution space, we’re starting from smaller strings and recursively generate larger strings.
public static void fourAB() {
fourAB("");
}
private static void fourAB(String soFar) {
if (soFar.length() == 4) {
System.out.println(soFar);
} else {
fourAB(soFar + "a");
fourAB(soFar + "b");
}
}
Recursive backtracking
Many of our exhaustive search problems will involve using a data structure to keep track of progress and build toward solutions. However, working with data structures is more complicated than working with numbers and strings due to reference semantics.
Let’s consider the rollDice method that prints out all of the outcomes of rolling 4 dice. We can visualize a decision tree representing the recursive process for evaluating the rollDice method.
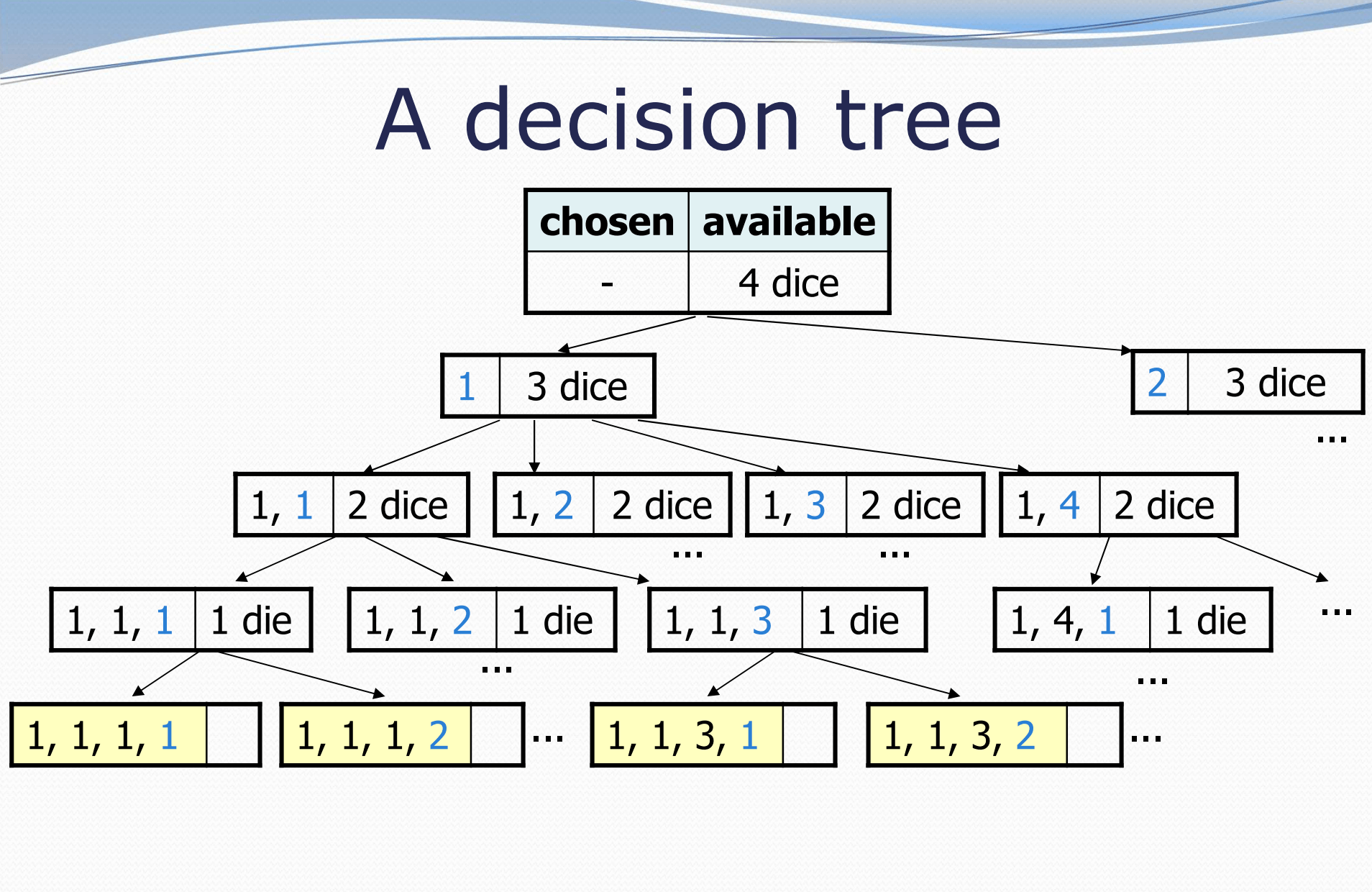
Note that this problem requires each recursive call to keep track of two parameters: the number of dice that still need to be rolled as well as the list of already-rolled dice outcomes.
public static void rollDice(int dice) {
rollDice(dice, new ArrayList<Integer>());
}
private static void rollDice(int dice, List<Integer> chosen) {
if (dice == 0) {
System.out.println(chosen);
} else {
chosen.add(1);
rollDice(dice - 1, chosen);
chosen.add(2);
rollDice(dice - 1, chosen);
chosen.add(3);
rollDice(dice - 1, chosen);
chosen.add(4);
rollDice(dice - 1, chosen);
chosen.add(5);
rollDice(dice - 1, chosen);
chosen.add(6);
rollDice(dice - 1, chosen);
}
}
We can reduce redundancy by using a for loop from 1–6 representing the possible dice rolls.
public static void rollDice(int dice) {
rollDice(dice, new ArrayList<Integer>());
}
private static void rollDice(int dice, List<Integer> chosen) {
if (dice == 0) {
System.out.println(chosen);
} else {
for (int i = 1; i <= 6; i++) {
chosen.add(i);
rollDice(dice - 1, chosen);
}
}
}
However, both of these programs exhibit a critical underlying bug due to Java reference semantics!
Describe the bug in your own words.
Consider what happens after we “roll” the first dice and add 1 to the chosen list of outcomes. The recursion here makes sense: we want to pass the updated list of chosen outcomes to the next recursive call. But when we return from the rollDice call responsible for the outcomes starting 1, the chosen list has been totally changed in the proces!
In order to address the unintended changes to the chosen list, we need to remove the choice that the current recursive method call was responsible for adding: the most recent outcome.
public static void rollDice(int dice) {
rollDice(dice, new ArrayList<Integer>());
}
private static void rollDice(int dice, List<Integer> chosen) {
if (dice == 0) {
System.out.println(chosen);
} else {
for (int i = 1; i <= 6; i++) {
chosen.add(i);
rollDice(dice - 1, chosen);
chosen.remove(chosen.size() - 1);
}
}
}
This leads us to a 3-step process for all of our recursive backtracking programs. For all possible options that need to be explored:
- Start by choosing the current option:
chosen.add(i) - Then, recursively explore that option:
rollDice(dice - 1, chosen) - After returning from the recursive call, unchoose the current option so that the data structure is restored to its original state before making the choice.
Full trace for rolling 2 dice.
Each indentation level represents a new recursive call.
rollDice(2, [])
i=1 -- add 1 to chosen, recurse on rollDice(1, [1])
i=1 -- add 1 to chosen, recurse on rollDice(0, [1, 1])
solution! print [1, 1]
i=2 -- add 2 to chosen, recurse on rollDice(0, [1, 2])
solution! print [1, 2]
i=3 -- add 3 to chosen, recurse on rollDice(0, [1, 3])
solution! print [1, 3]
i=4 -- add 4 to chosen, recurse on rollDice(0, [1, 4])
solution! print [1, 4]
i=5 -- add 5 to chosen, recurse on rollDice(0, [1, 5])
solution! print [1, 5]
i=6 -- add 6 to chosen, recurse on rollDice(0, [1, 6])
solution! print [1, 6]
i=2 -- add 2 to chosen, recurse on rollDice(1, [2])
i=1 -- add 1 to chosen, recurse on rollDice(0, [2, 1])
solution! print [2, 1]
i=2 -- add 2 to chosen, recurse on rollDice(0, [2, 2])
solution! print [2, 2]
i=3 -- add 3 to chosen, recurse on rollDice(0, [2, 3])
solution! print [2, 3]
i=4 -- add 4 to chosen, recurse on rollDice(0, [2, 4])
solution! print [2, 4]
i=5 -- add 5 to chosen, recurse on rollDice(0, [2, 5])
solution! print [2, 5]
i=6 -- add 6 to chosen, recurse on rollDice(0, [2, 6])
solution! print [2, 6]
i=3 -- add 3 to chosen, recurse on rollDice(1, [3])
i=1 -- add 1 to chosen, recurse on rollDice(0, [3, 1])
solution! print [3, 1]
i=2 -- add 2 to chosen, recurse on rollDice(0, [3, 2])
solution! print [3, 2]
i=3 -- add 3 to chosen, recurse on rollDice(0, [3, 3])
solution! print [3, 3]
i=4 -- add 4 to chosen, recurse on rollDice(0, [3, 4])
solution! print [3, 4]
i=5 -- add 5 to chosen, recurse on rollDice(0, [3, 5])
solution! print [3, 5]
i=6 -- add 6 to chosen, recurse on rollDice(0, [3, 6])
solution! print [3, 6]
i=4 -- add 4 to chosen, recurse on rollDice(1, [4])
i=1 -- add 1 to chosen, recurse on rollDice(0, [4, 1])
solution! print [4, 1]
i=2 -- add 2 to chosen, recurse on rollDice(0, [4, 2])
solution! print [4, 2]
i=3 -- add 3 to chosen, recurse on rollDice(0, [4, 3])
solution! print [4, 3]
i=4 -- add 4 to chosen, recurse on rollDice(0, [4, 4])
solution! print [4, 4]
i=5 -- add 5 to chosen, recurse on rollDice(0, [4, 5])
solution! print [4, 5]
i=6 -- add 6 to chosen, recurse on rollDice(0, [4, 6])
solution! print [4, 6]
i=5 -- add 5 to chosen, recurse on rollDice(1, [5])
i=1 -- add 1 to chosen, recurse on rollDice(0, [5, 1])
solution! print [5, 1]
i=2 -- add 2 to chosen, recurse on rollDice(0, [5, 2])
solution! print [5, 2]
i=3 -- add 3 to chosen, recurse on rollDice(0, [5, 3])
solution! print [5, 3]
i=4 -- add 4 to chosen, recurse on rollDice(0, [5, 4])
solution! print [5, 4]
i=5 -- add 5 to chosen, recurse on rollDice(0, [5, 5])
solution! print [5, 5]
i=6 -- add 6 to chosen, recurse on rollDice(0, [5, 6])
solution! print [5, 6]
i=6 -- add 6 to chosen, recurse on rollDice(1, [6])
i=1 -- add 1 to chosen, recurse on rollDice(0, [6, 1])
solution! print [6, 1]
i=2 -- add 2 to chosen, recurse on rollDice(0, [6, 2])
solution! print [6, 2]
i=3 -- add 3 to chosen, recurse on rollDice(0, [6, 3])
solution! print [6, 3]
i=4 -- add 4 to chosen, recurse on rollDice(0, [6, 4])
solution! print [6, 4]
i=5 -- add 5 to chosen, recurse on rollDice(0, [6, 5])
solution! print [6, 5]
i=6 -- add 6 to chosen, recurse on rollDice(0, [6, 6])
solution! print [6, 6]
A very useful skill for helping you write recursive backtracking is identifying how this trace relates to the code that generated it. Some questions you should try to answer to help with this connection:
- Where does the base case appear in the trace?
- How is the number of choices at each level of recursion determined by the code?
- What code needs to be written to modify the parameters for the next recursive call?