Link Search Menu Expand Document
CSE 143

Huffman Coding

Compressing data with binary trees and collections.

ed Workspace

Table of contents

  1. Character representation
  2. Algorithm
    1. Counting characters
    2. Initializing a priority queue
    3. Combining nodes
    4. Generating Huffman codes
  3. HuffmanCode
    1. HuffmanNode
    2. Method summary
    3. Line-based processing
    4. Translate example
  4. BitInputStream
  5. Grading
  6. Reflection
  7. Submission

Huffman coding is an algorithm devised by David Huffman in 1952 for compressing data, reducing the file size of an image (or any file) without affecting its quality. Unbelievably, this algorithm is still used today in a variety of very important areas. For example, MP3 files and JPEG images both use Huffman coding. We’ll use Huffman coding to compress text files composed of English characters.

Character representation

Huffman coding relies on the key observation that some characters appear more often than others. The characters that appear most often are, in terms of frequency, more important than the characters that appear less often.

Earlier, we saw that every char has an equivalent int value between 0 and 255. Computers work with integers in binary format (1’s and 0’s). Binary is similar to normal decimal numbers except it is base2 instead of base10.

For example, the decimal number 120410 is read as 1 · 103 + 2 · 102 + 0 · 101 + 4 · 100. Similarly, we can represent the decimal number 9710 in binary as 011000012 since 9710 is 0 · 27 + 1 · 26 + 1 · 25 + 0 · 24 + 0 · 23 + 0 · 22 + 0 · 21 + 1 · 20.

All Java char values can be written using exactly 8 binary digits (bits). This encoding is called ASCII.

The following string data contains 240 characters: 229 a’s, 4 b’s, 3 c’s, and 2 d’s. If each character is represented in Java as an ASCII char, then the total file size is 2560 bits.

bbbbaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
cccaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
ddaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa

However, since a is by far the most frequent character, then it’s better to represent a with the fewest possible bits to save space (followed by b, c, and then d). The following Huffman coding is a more efficient representation of the same string data.

  • a can be represented with a one-bit code, 12.
  • b can be represented with a two-bit code, 002.
  • c can be represented with a three-bit code, 0112.
  • d can be represented with a four-bit code, 0102.

The resulting file size is only 255 bits, compressing the data by a factor of 10!

Why not want represent b with a one-bit code, 02?

That could result in ambiguity when decoding the string. For example, given the encoded data, 0112, there are now two possible interpretations!

  1. c
  2. baa

Algorithm

Consider the following example found in the simple-spec-example.txt file.

aba ab cabbb

Counting characters

The example contains the characters a, b, c, and the space character.

Character’ ‘‘a’‘b’‘c’
Count2451

Initializing a priority queue

A priority queue will be used to keep track of character counts. Priority queues are a special type of queue ordered by the priority value (e.g. character count) instead of FIFO order, so the remove method removes the highest priority element from the queue rather than the oldest element.

In order to represent the (char, int) pair representing the character together with its frequency, introduce a new data type called HuffmanNode. For Huffman coding, rather than remove the highest-frequency character, remove the character with the lowest frequency first.

Initialized priority queue

Note that the only characters from the file with non-zero frequencies were these characters, so those are the only ones we created HuffmanNodes for

Combining nodes

Given the priority queue of the nodes, our goal is to form a Huffman tree representing the relative importance of each character. Repeatedly remove the smallest two nodes and create a new node with them as children.

  1. First, remove the smallest two nodes from the priority queue.

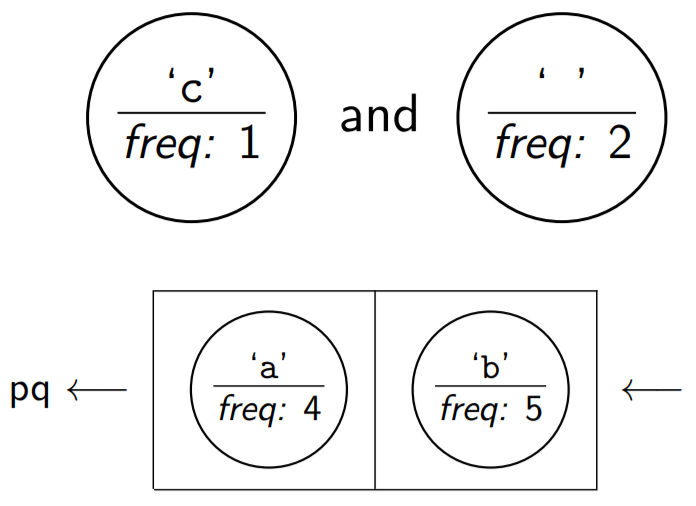
    Remove two smallest

  2. Then, create a new node. The frequency is the sum of the two nodes.

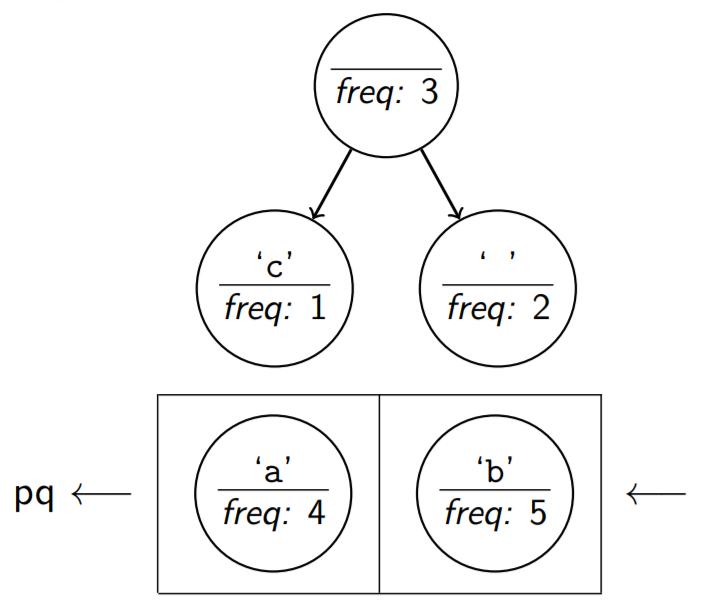
    Combine them together

  3. Add the new node back to the priority queue.

    Add back to priority queue

Repeat this process until there is only one node in the priority queue representing the complete Huffman tree.

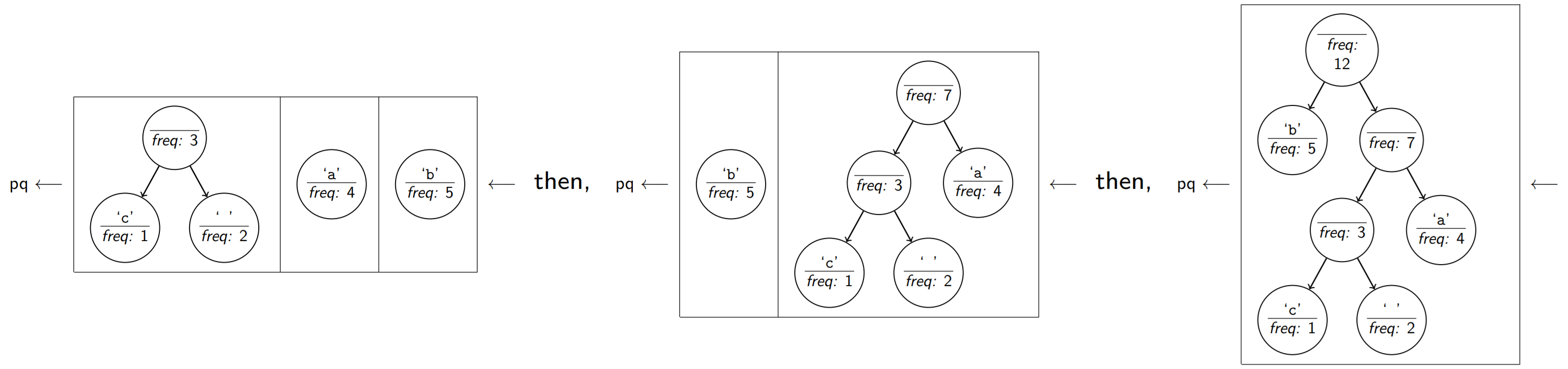
Combine nodes until complete

Generating Huffman codes

At this point, the frequencies of the letters have already been taken into account, so character counts are no longer necessary. The resulting Huffman tree represents the optimal encodings for the data file. Notice that the only actual information is in the leaves of the tree.

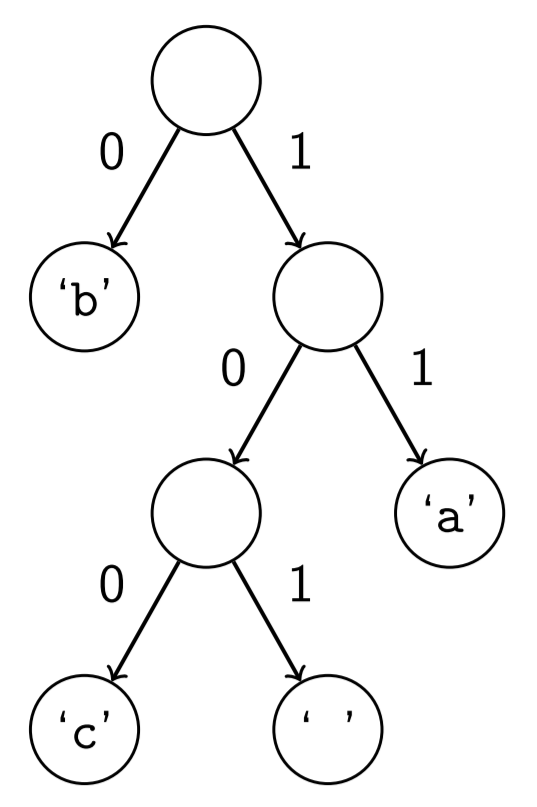
Huffman tree

To determine the Huffman code for a character, traverse the tree from the root to the node with the letter in it. For left branches, print 0. For right branches, print 1. For example, the character c would be represented with the three-bit code 100, because it is located in the node right, left, left of the overall root.

Output the tree in the following standard code file format consisting of pairs of lines, where the first line in the pair is the ASCII value of the character and the second line is the Huffman code for that character. Each pair should appear in traversal order. For example, the simple-spec-example.code file contains the following contents.

98
0
99
100
32
101
97
11

HuffmanCode

Implement the HuffmanCode class representing a Huffman code for a particular message as a Huffman tree generated according to the described algorithm. The HuffmanCode class includes a private static inner class called HuffmanNode, representing individual nodes in the Huffman tree.

There are two separate parts to the HuffmanCode class.

  1. Creating a Huffman code with the frequencies constructor and save method.
  2. Decompressing a message with the input constructor and translate method.

HuffmanNode

The contents of the HuffmanNode class are up to you, but it should have at least one constructor used by the HuffmanCode class and all node fields must be declared public. HuffmanNode should not contain any of the actual algorithm.

Since the priority queue will ultimately be declared as PriorityQueue<HuffmanNode>, the HuffmanNode class must implement Comparable<HuffmanNode>. Use the frequency of the subtree to determine its ordering relative to other subtrees, with lower frequencies considered “less than” higher frequencies. If two frequencies are equal, the nodes are considered equal as well.

Method summary

public HuffmanCode(int[] frequencies)
Initializes a new HuffmanCode object using the described algorithm given an array of frequencies where frequences[i] represents the count of the character with ASCII value i. Use a PriorityQueue to build the Huffman code.
public HuffmanCode(Scanner input)
Initializes a new HuffmanCode object by reading in a previously saved code file. Assume the Scanner is not null and always contains data encoded in the standard format. Since frequencies are irrelevant for this part, all node frequencies should be set to some standard value such as 0 or -1.
public void save(PrintStream output)
Stores the current Huffman codes to the given output stream in the standard format.
public void translate(BitInputStream input, PrintStream output)
Reads individual bits from the input stream and writes the corresponding characters to the output. Stops reading when the input is empty. Assume the input stream is compatible with this Huffman tree.

Line-based processing

When implementing the Scanner constructor, do not call nextInt() to read the integer and nextLine(). Mixing token-based reading and line-based reading can cause problems. Instead, use only line-based reading and call Integer.parseInt when int values are needed.

int asciiValue = Integer.parseInt(input.nextLine());
String code = input.nextLine();

Translate example

Algorithm for translate
  1. Begin at the top of the tree.
  2. For each bit in the input, go left for 0 and go right for 1.
  3. At a leaf node, write the integer code to the output.
  4. Repeat this process so long as there are still more bits to read.

Suppose we have the following simple-spec-example.short message encoded using the simple-spec-example.code Huffman coding.

1101110111010110011000

The trace below diagrams the steps determining each character in the short message, resulting in the decompressed message, “aba ab cabbb”.

  1. Read 1, go right. Read 1, go right. ‘a’ is a leaf. Output ‘a’. Remaining input is 01110111010110011000.
  2. Read 0, go left. ‘b’ is a leaf. Output ‘b’. Remaining input is 1110111010110011000.
  3. Read 1, go right. Read 1, go right. ‘a’ is a leaf. Output ‘a’. Remaining input is 10111010110011000.
  4. Read 1, go right. Read 0, go left. Read 1, go right. ‘ ‘ is a leaf. Output ‘ ‘. Remaining input is 11010110011000.
  5. Read 1, go right. Read 1, go right. ‘a’ is a leaf. Output ‘a’. Remaining input is 010110011000.
  6. Read 0, go left. ‘b’ is a leaf. Output ‘b’. Remaining input is 10110011000.
  7. Read 1, go right. Read 0, go left. Read 1, go right. ‘ ‘ is a leaf. Output ‘ ‘. Remaining input is 10011000.
  8. Read 1, go right. Read 0, go left. Read 0, go right. ‘c’ is a leaf. Output ‘c’. Remaining input is 11000.
  9. Read 1, go right. Read 1, go right. ‘a’ is a leaf. Output ‘a’. Remaining input is 000.
  10. Read 0, go left. ‘b’ is a leaf. Output ‘b’. Remaining input is 00.
  11. Read 0, go left. ‘b’ is a leaf. Output ‘b’. Remaining input is 0.
  12. Read 0, go left. ‘b’ is a leaf. Output ‘b’. Remaining input is empty.

When implementing translate, do not call System.out.print and instead write to the given output. The PrintStream class contains a write method that accepts an int as a parameter. Be careful with using recursion since Java may throw a StackOverflowError when it exceeds a certain number of recursive calls. For a large message, there may be hundreds of thousands of characters to decode.

BitInputStream

The provided BitInputStream class reads data bit-by-bit for the translate method in HuffmanCode. The interface for BitInputStream looks very much like a Scanner, so it should be used in a similiar fashion.

public int nextBit()
Returns the next bit in the input stream. Throws a NoSuchElementException if there are no more bits.
public boolean hasNextBit()
This method returns true if the input stream has at least one more bit and false otherwise.

Grading

Avoid unnecessary logic such as extra base cases or recursive cases. Use the x = change(x) pattern to simplify code and use the Output Comparison Tool to check the output format! Remember to declare variables with their interface types when possible, so PriorityQueue variables should be delcared using the Queue interface type.

The Huffman coding for a given message is not necessarily unique. If implemented exactly as specified, then you should get exactly the same tree so long as, when combining nodes, the first node removed becomes the left subtree and the second node removed becomes the right subtree.

Reflection

Create a new file reflection.txt and write a paragraph-long reflection answering the following questions (along with anything else you find appropriate):

  1. What did you learn this week?
  2. What did you enjoy in the course this week?
  3. What did you find challenging or frustrating this week?
  4. What did you find particularly helpful for your learning this week?

Submission

In addition to the completed program, submit files named secretmessage.short and secretmessage.code that represent a secret compressed message from you to your TA. The message can be anything you want as long as it is not offensive.

Submit HuffmanCode.java, secretmessage.short, secretmessage.code, and reflection.txt to Grade-It!