Binary search; complexity

ed Lesson

Table of contents

• Complexity
• Runtime analysis
• Understanding
• Modeling
• Formalizing
• Binary search

Complexity

Beyond whether or not a program is correct, computer scientists are often concerned about the complexity of a program. We actually already have quite a bit of experience with one particular kind of complexity that arises from how we design abstractions for our programs. For instance, pulling repeated code out into a method gives it a name and makes it easier for the reader to understand the behavior of the program. Cognitive complexity is about how easy it is to understand a program.

Code is just one way for programmers to communicate ideas to others, and writing code requires worrying about cognitive complexity. But programmers also communicate ideas to others in terms of algorithms, the more generalizable list of steps behind the code. Whereas code is specific to a particular programming language, we can communicate algorithms in natural languages like English too. Whenever we’re describing a program to someone else, we’re really describing an algorithm.

We can analyze algorithms in several ways.

Time complexity

How much time does it take for the algorithm to evaluate?

Space complexity

How much memory does the algorithm require?

Increasingly, computer scientists are also growing more concerned about social impact: beyond the computer, how do algorithms affect the rest of the world? However, the primary discourse in mainstream computer science is still focused around time complexity, so that’s what we’ll emphasize in this course.

Runtime analysis

Runtime analysis is the process of determining the time complexity of an algorithm.

Like code, complexity is all about communicating ideas about algorithms to others. This communication is most effective when it is (1) simple and (2) easy to compare. Computer scientists follow a three-step process to effectively communicate ideas about time complexity.

Runtime analysis process

1. Understanding the behavior or implementation details of the algorithm.
2. Modeling the number of steps or operations needed to evaluate an algorithm in terms of the size of the input.
3. Formalizing the result in precise English or mathematical notation.

Understanding

Earlier, we saw that the list contains method (which calls indexOf) could be very slow. Let’s apply the runtime analysis process to analyze a slightly simpler algorithm that returns the index of target in an int[] array or -1 if target is not in the array.

static int indexOf(int[] array, int target) {
    for (int i = 0; i < array.length; i++) {
        if (array[i] == target) {
            return i;
        }
    }
    return -1;
}

The behavior of the indexOf algorithm depends on the input values.

Modeling

Modeling is about counting the number of steps or operations, such as assignments, boolean evaluations, arithmetic operations, method calls, etc.

int a = 4 * 6;
int b = 9 * (a - 24) / (9 - 7);

The first assignment to a takes one step to compute 4 * 6 and one more step to assign the result, 24, to the variable a.

How do we apply this thinking to indexOf?

for (int i = 0; i < array.length; i++) {
    if (array[i] == target) {
        return i;
    }
}

The goal of time complexity analysis is to make an argument about the running time of an algorithm. In most cases, we only care about what happens for very large N (asymptotic behavior). We want to consider what types of algorithms would best handle big amounts of data, such as simulating the folding of very long chains of amino acids in proteins.

The number of steps it takes to compute indexOf is primarily determined by the length of the array, which we’ll call N.

Asymptotic analysis

Describes the step count in terms of N, the size of the input, as N becomes very large. The differences between algorithms are easier to appreciate with more data since. A longer array may result in more iterations of the for loop.

When we talk about runtime in terms of “iterations of a loop”, we’re making an important conceptual simplification.

Cost model

Instead of counting every single operation, choose an operation to approximate the overall order of growth. The number of iterations of the for loop is an appropriate cost model since it is directly correlated to the total number of steps that it takes to evaluate the algorithm.

Case analysis

Accounts for variation in step count based on interactions between factors. Even with a very long array, it’s possible that the algorithm exits the for loop in the very first iteration if the array[0] == target. But it’s also possible that the algorithm increments the counter and loops through the entire array without finding the target.

Formalizing

To summarize our findings, we can say the following about the runtime of indexOf.

Simple English

1. In the worst case (when the target is not in the array), the number of steps that it takes to evaluate indexOf is directly correlated with N, the length of the array.
2. In the best case (when array[0] == target), it takes about 4 steps to evaluate indexOf regardless of the length of the array.

This description succinctly captures the different factors that can potentially affect the runtime of indexOf. While this description captures all of the ideas necessary to convey the key message, computer scientists will typically enhance this description with mathematics to capture a more general geometric intuition about the runtime.

Order of growth

1. In the worst case, the order of growth of the runtime of indexOf is linear with respect to N, the length of the array.
2. In the best case, the order of growth of the runtime of indexOf is constant with respect to N, the length of the array.

The order of growth relates the size of the input to the time that it takes to evaluate the algorithm on that input. The below log-log plot compares the typical orders of growth.¹

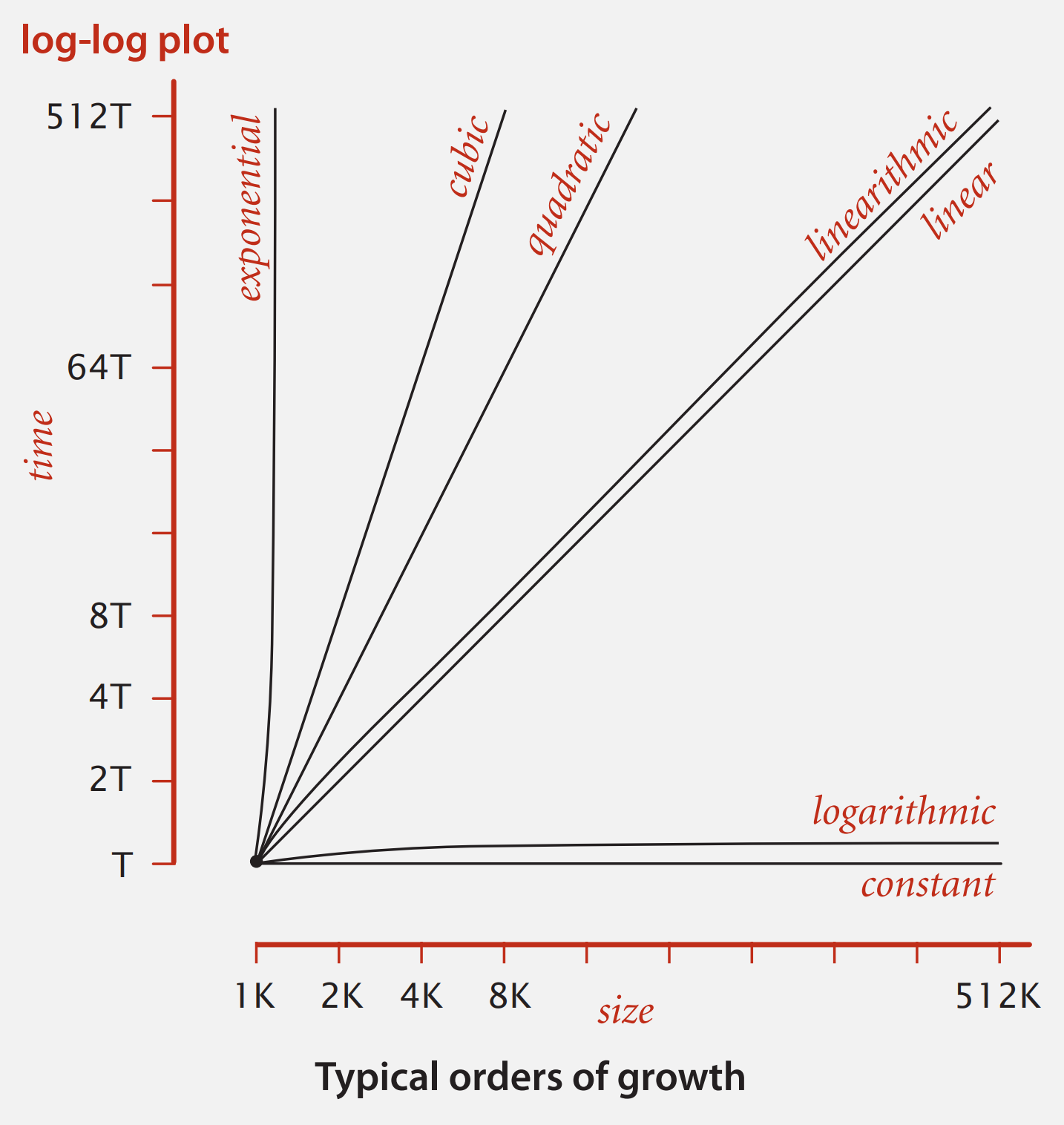
Mathematicians first formally described the idea of order of growth using big-O (“big oh”) notation over 100 years ago. Computer scientists adopted this notation for runtime analysis in the 1970s. However, many programmers nowadays misuse big-O notation. The mathematical notation that best represents our “directly correlates” idea of orders of growth is big-Θ (“big theta”) notation.

Big-Θ notation

1. In the worst case, the runtime of indexOf is in Θ(N) [the family of functions whose order of growth is linear] with respect to N, the length of the array.
2. In the best case, the runtime of indexOf is in Θ(1) [the family of functions whose order of growth is constant] with respect to N, the length of the array.

This notation is both simple and easy to compare!

Binary search

It turns out that the best known algorithm for many important problems takes exponential time, making them impossible to solve in practice. To put it into perspective, an input of size N = 100 (e.g. array.length == 100) that takes a linear-time algorithm less than 1 second to evaluate would take an exponential-time algorithm about 10¹⁷ years to compute a result.

Looking back at the log-log plot, the improvement from exponential-time to linear-time is the same magnitude of improvement as linear-time to logarithmic-time. It’s for this reason that TreeSet.contains, a logarithmic-time algorithm, is so much faster than ArrayList.contains, a linear-time algorithm, for solving the Shakespeare text processing problem. Let’s apply the runtime analysis process on binary search, the fundamental idea behind TreeSet.contains, in the context of sorted arrays.

Suppose we have a sorted array of integers. Binary search is an efficient algorithm for returning the index of the target value in a sorted array.

static int binarySearch(int[] sorted, int target) {
    // Start looking at the whole sorted array
    int low = 0;
    int high = sorted.length - 1;

    // while low and high haven't met yet, there are still more indices to search
    while (low <= high) {
        // compute middle index and value
        int mid = low + (high - low) / 2;

        if (sorted[mid] < target) {
            low = mid + 1;
        } else if (sorted[mid] > target) {
            high = mid - 1;
        } else {
            return mid;
        }
    }
    return -1;
}

In each iteration of the loop, half of the elements under consideration can be discarded. The number of iterations of the while loop can be phrased as, “How many times do we need to divide N (the length of the sorted array) by 2 until only 1 element remains?” This is the definition of the binary logarithm, or log₂.

Alternatively, we could rephrase the question as, “How many times do we need to multiply by 2 to reach N?” To solve for 2^x = N, we get x = log₂ N.