Prefix Operations and Tries
We’ve explored several different implementations for the Set and Map ADTs. So far, our discussion of data structures has focused primarily on developing generalizable solutions. Search trees can accept any Comparable data type; hash tables can accept any class with a hashCode and an equals method. But our runtime analysis for these data structures have overlooked one important factor: the time it takes to compare two keys.
For data types like integers, the comparison cost is constant: the largest Java integer is 2,147,483,647. This integer is 10 decimal digits long or 31 binary digits. Since computers typically compare numbers by their binary digits, we can assert that integer comparison takes constant time because there are at most 31 binary digits that need to be compared.
However, this isn’t true for strings. Since there can be hundreds, thousands, or millions of characters in a string, the time it takes to compare two strings depends on the length, L, of the strings.
static int compareTo(String s1, String s2) {
String s1, s2;
int L = Math.min(s1.length(), s2.length());
for (int k = 0; k < L; k += 1) {
if (s1.getChar(k) != s2.getChar(k)) {
return s1.getChar(k) - s2.getChar(k);
}
}
return s1.length() - s2.length();
}
The equals method does something similar except it returns a boolean rather than an integer.
Taking into account the length of strings, let’s redo our analysis for HashSet<String>. Let N be the total size of the set (ie, the number of strings). Let L be the length of the longest string in the set.
Give a big-O runtime bound for the contains method.
O(NL) since potentially all of the strings could collide in a single bucket. If each string in the bucket happens to be of length L and shares all the same characters except for the last character, it can take O(L) time to compare each string.
In practice, we never really run into this exact scenario since strings that differ only in the last character tend to have different hash codes.
Specialized Data Structures
Suppose we know that our keys aren’t even strings but are just individual ASCII characters. We can implement the Map ADT with just an array; the index for each element represents the char key (ranging from 0–127) while the value at that index is the value associated with that key. The idea of indexing into an array using the key itself may remind you of the DirectAccessMap we used in lecture to introduce hash maps. Here’s an implementation of this idea.
public class DataIndexedCharMap<V> {
private V[] items;
public DataIndexedCharMap(int R) {
items = (V[]) new Object[R]; // 128 for ASCII
}
public void put(char c, V value) {
items[c] = value;
}
public V get(char c) {
return items[c];
}
}
As before, this DataIndexedCharMap<V> is a specialized data structure with appealing performance: get(c) is a constant-time array access, while put(c, val) is a constant-time array assignment.
Tries
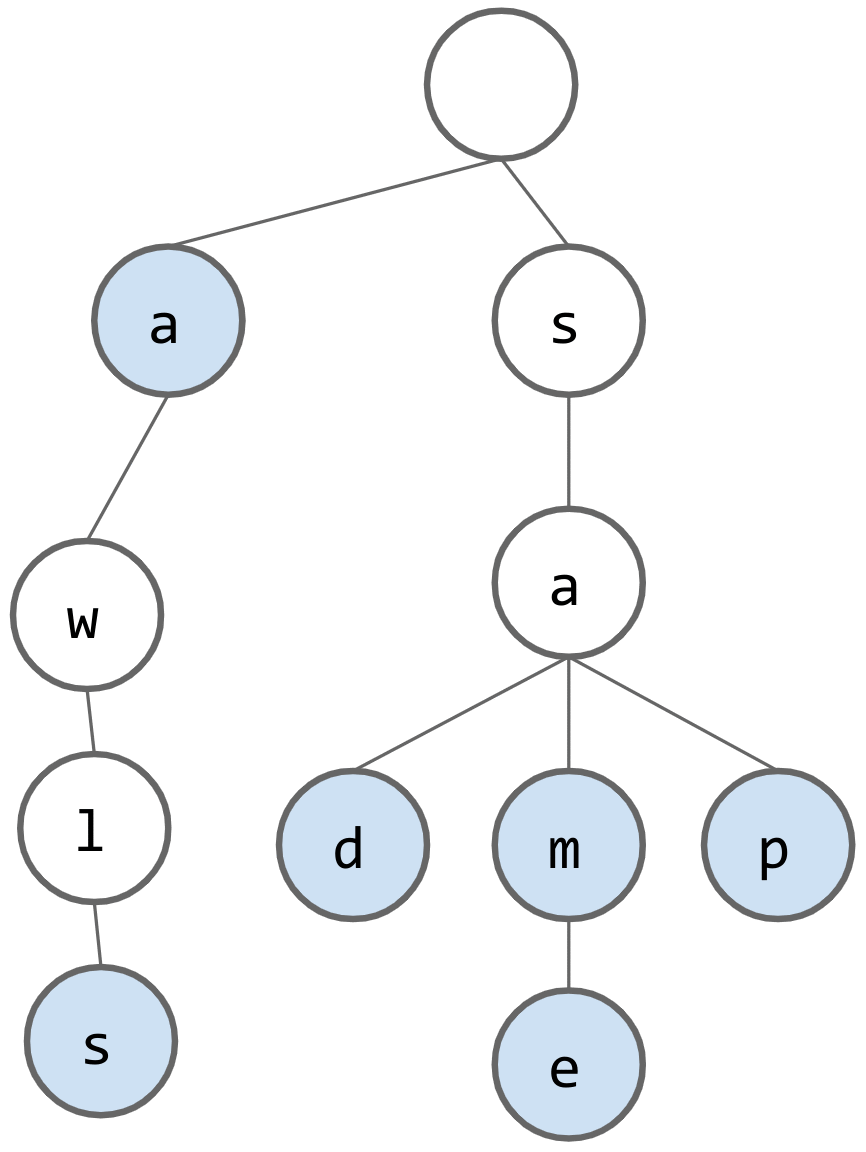
Along the same lines, suppose we want to store strings of variable length. One solution is called a “trie” (pronounced “try”). The basic idea behind a trie is to store each character of a string as a node in a tree. The result is no longer a binary (2-way) tree, but instead a 128-way tree in the case of ASCII strings.
The following trie contains the words “sam” and “sad”.
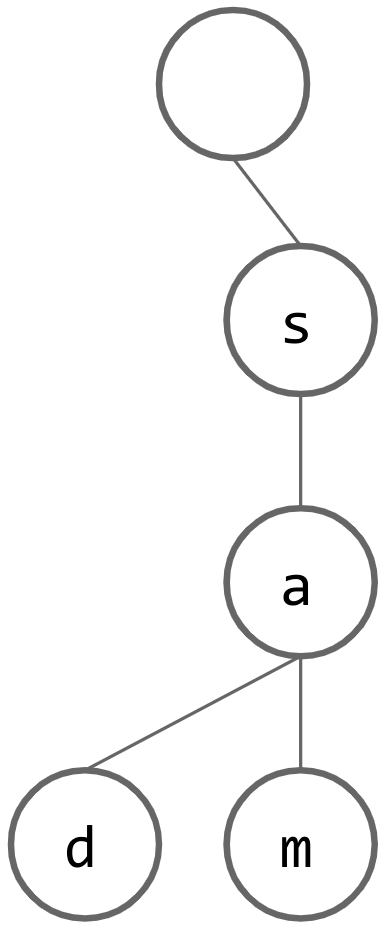
What should the trie look like after inserting "sap", "same", and "awls"?
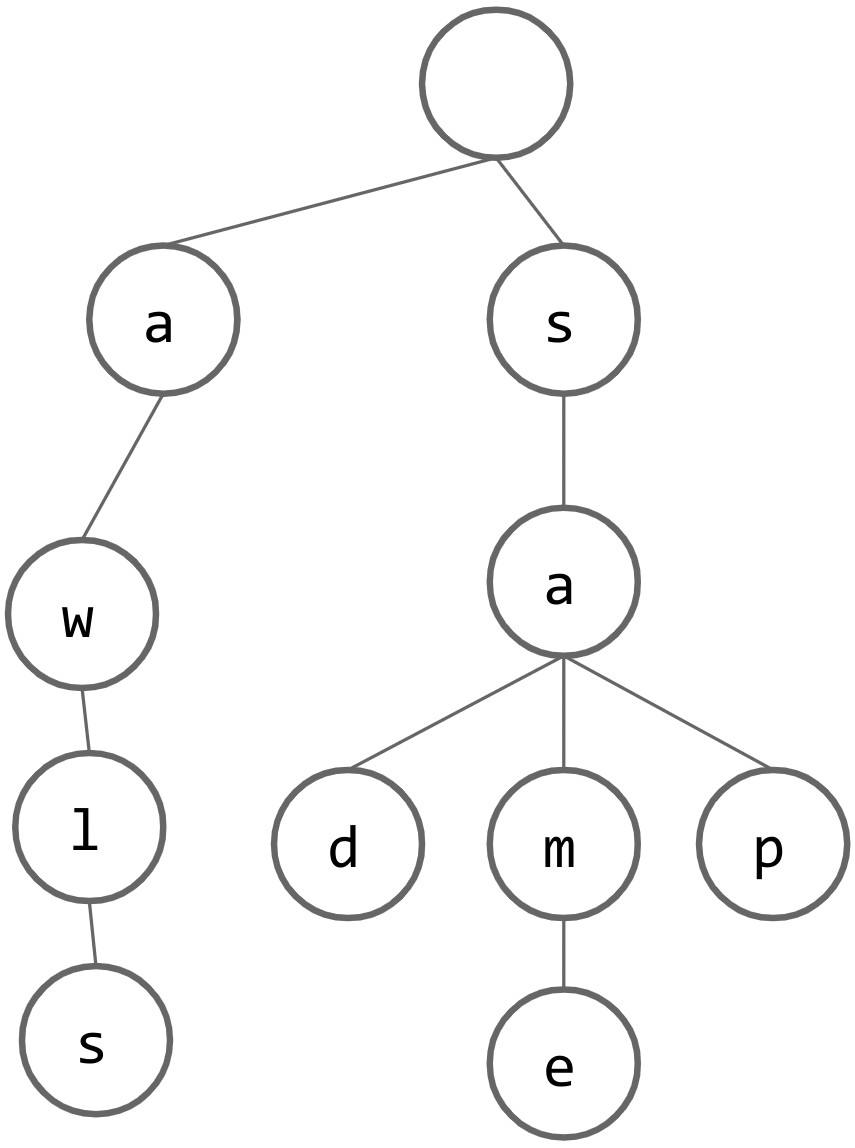
What should the trie look like after inserting "a"?
We need some way to distinguish between nodes that are valid words and nodes that are not valid words. We can add a boolean variable to each node marking whether or not it is a valid word.