B-Trees
Complete the Reading Quiz by 3:00pm before lecture.
In lecture, we discovered that the runtime of many binary search tree operations were defined in terms of its height; for example, find() was Theta(height). Unfortunately, we also discovered that trees can span a spectrum of shapes from the best case “bushy tree” to a worst case “spindly tree”. These aren’t formal terms, but we can start to build a more precise understanding by studying the runtime complexity of common operations like searching for an item.
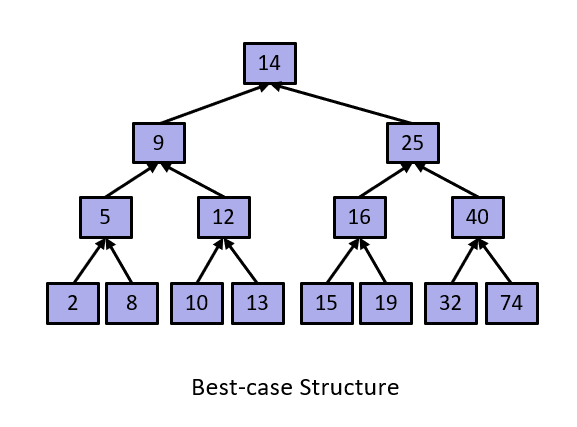
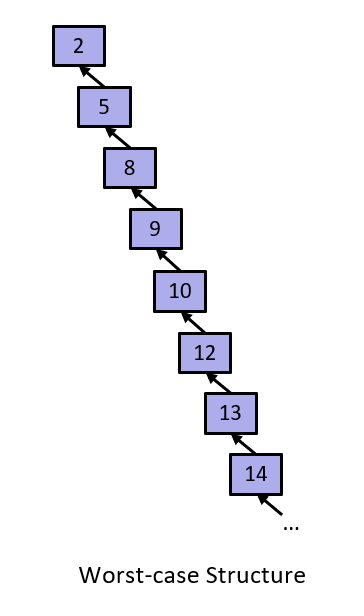
We can identify the difference between these two cases by describing the relationship between the height of the tree and the total number of nodes in the tree.
- Path
- A connected sequence of edges that join parent and child nodes.
- Height of a tree
- The number of edges on the longest path between the root node and any leaf.
Let H(N) be the height of a tree with N nodes. Give H(N) in Big-Theta notation for bushy trees and for spindly trees.
In the best case of a bushy tree, the height of the tree H(N) is in Theta(log N). In the worst case of a spindly tree, the height of the tree H(N) is in Theta(N).
The difference between the best-case height and the worst-case height affects the runtime of all BST operations, including contains, find, add, and remove. The height of the tree determines the worst-case order of growth for these operations, but it’s also useful to get a sense of the average case as another metric for running time.
- Depth of a node
- The number of edges on the path between the root and the single given node.
- Average depth of a tree
- The average depth of the given tree’s nodes.
If the height of a tree determines the worst-case scenario, then the average depth of a tree can help us analyze the average case. We’ll explore this idea further in lecture but, first, let’s step back and consider how to express these ideas in terms of asymptotic notation.
Big-O is not Worst Case
Consider the following statements about the height of a binary search tree.
- Worst case BST height is in Theta(N).
- BST height is in O(N).
- BST height is in O(N2).
Which of the above statements are true?
All of them are true!
- A worst case (spindly tree) has a height that grows exactly linearly—hence, Theta(N).
- All BSTs have a height that grows linearly or better—O(N).
- All BSTs have a height that grows quadratically or better—O(N2)
Some statements, however, are more specific than others. Earlier, we informally referred to Big-O notation as a less-than relationship. Statements 2 and 3 were both true: the height of a BST is in O(N) and also in O(N2). But we could also say that the height of a BST is in O(N3), O(2N), O(NN), and so forth. In this way, Big-O is less descriptive than Big-Theta: we can say that the worst case height of a BST is in Theta(N) and the reader will know that must be the exact worst case order of growth.
Mathematically, Big-O does not imply worst case though it is often used this way in the real world. Big-O is still useful for making blanket statements about the runtime in all cases, best and worst inclusive. For example, both of following statements are true:
- “The height of a BST is in O(N)”
- “The worst case height of a BST is in Theta(N)” The second statement is more precise, but we often see the first statement interpreted as if it were the second; don’t fall into this trap! There are algorithms and data structures where we can’t easily find or prove the Big-Theta bound, so the looseness of the Big-O notation lets us state what we know to be true without making false claims.