Seam Finding
Finding seams, as a reduction to the shortest path problem.
Table of contents
Finding Seams
After calculating the energy of each pixel, the resizing algorithm needs to find the minimum-energy seam. To recap, a seam is a path of adjacent or diagonally-adjacent pixels from one side of the image to the other, with exactly 1 pixel from each row/column, for vertical/horizontal seams respectively. (Opposite sides of an image are not adjacent, so seams cannot wrap around the image.)
As mentioned previously, this subproblem looks much like a regular shortest path problem, but there are three important differences:
- Each edge weight is based on a vertex (pixel) rather than the edge itself.
- The goal is to find the shortest path from any of the pixels in the top row to any of the pixels in the bottom row.
- The graph has a regular structure: there is a downward edge from pixel to pixels , , and , assuming that the coordinates are in the prescribed ranges. (As an aside, this means that the graph is a directed acyclic graph (DAG).)
Vertical Example
The findVerticalSeam method returns an array of length such that entry is the column number of the pixel to be removed from row of the image. Consider the 6-by-5 image (6x5.png) with RGB values shown in the table below.
| (78, 209, 79) | (63, 118, 247) | (92, 175, 95) | (243, 73, 183) | (210, 109, 104) | (252, 101, 119) |
| (224, 191, 182) | (108, 89, 82) | (80, 196, 230) | (112, 156, 180) | (176, 178, 120) | (142, 151, 142) |
| (117, 189, 149) | (171, 231, 153) | (149, 164, 168) | (107, 119, 71) | (120, 105, 138) | (163, 174, 196) |
| (163, 222, 132) | (187, 117, 183) | (92, 145, 69) | (158, 143, 79) | (220, 75, 222) | (189, 73, 214) |
| (211, 120, 173) | (188, 218, 244) | (214, 103, 68) | (163, 166, 246) | (79, 125, 246) | (211, 201, 98) |
The minimum energy vertical seam is highlighted in blue. In this case, the method findVerticalSeam returns the array [4, 4, 3, 2, 2] because the pixels in the minimum energy vertical seam are .
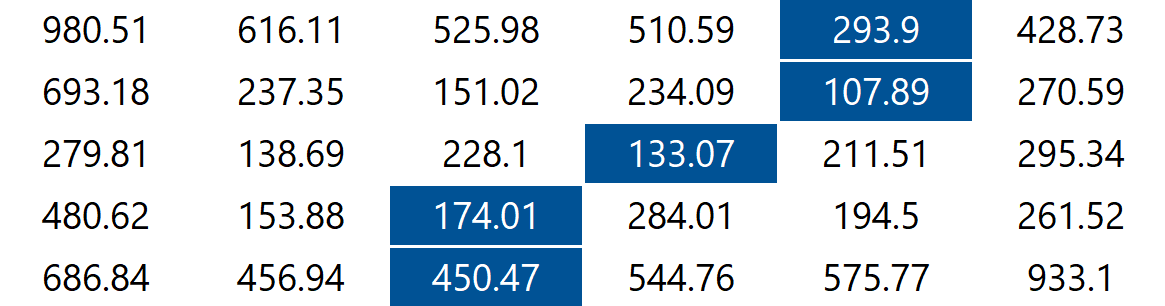
When there are multiple vertical seams with minimal total energy, your method can return any such seam.
Horizontal Example
The behavior of findHorizontalSeam is analogous to that of findVerticalSeam except that it should return an array of length such that entry is the row number of the pixel to be removed from column of the image. For the 6-by-5 image, the method findHorizontalSeam returns the array [2, 2, 1, 2, 1, 1] because the pixels in the minimum energy horizontal seam are .
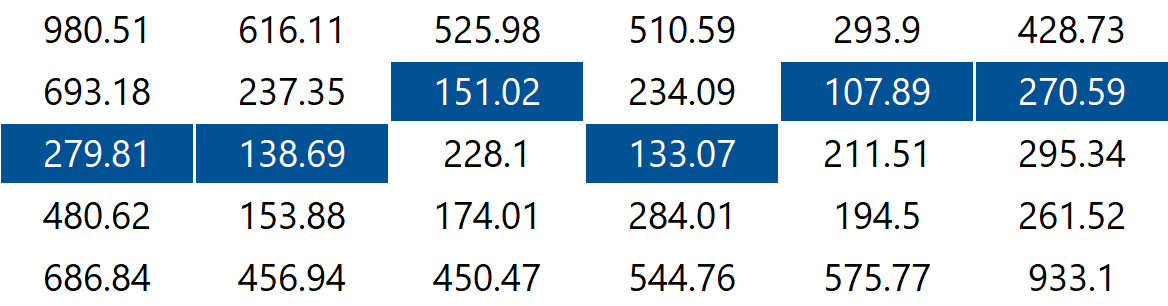
Dijkstra Seam Finder
- Task
- Implement
DijkstraSeamFinder.
Reduction
- Task
- Implement the reduction from the seam finding problem to the single-source single-destination shortest path problem.
We will reduce the seam finding problem into one solvable by DijkstraShortestPathFinder; this can be broken up into two major components:
- Creating the
Graphimplementation thatDijkstraShortestPathFinderwill operate on. - Setting up the actual reduction:
- Any logic required to transform the method’s input into input for
DijkstraShortestPathFinder. This includes instantiating the graph implementation and choosing the start and end vertices. - Any logic required to convert the output of
DijkstraShortestPathFinderinto the format required for the method’s output.
- Any logic required to transform the method’s input into input for
Depending on your preferences, you may find it easiest to start drafting up the graph implementation first, then update it as required to fit the rest of the reduction; or to work the other way around by starting with the surrounding reduction, then creating a graph to match.
Either way, we recommend reading through the rest of the instructions before starting to write any code. These tasks are related, so you will likely find yourself going back and forth between them a bit.
Notes:
- The path finder needs a single vertex to start on and a single vertex to end on. In the seam carving problem, there are multiple possible first and last pixels to choose. The hardest part of the reduction is figuring out how to augment the graph to allow the path finder to discover all valid seams.
DijkstraShortestPathFinderincludes aShortestPathFinderfield initialized by its constructor. On the grader, this field will contain the solution implementation, so you should use it rather than instantiating newDijkstraShortestPathFinders so that you don’t get penalized again for any bugs or inefficiencies left over from previous assignments.
Graph
- Task
- Implement the graph representation that the seam finder will use.
Here’s a rough graph specification for finding vertical seams:
- Vertices represent pixels.
- Edges exist from a pixel to its 3 downward neighbors.
- Edges have weight representing energy.
- The shortest (least total weight) path from top to bottom represents the minimum-energy seam.
Notes:
- It will also be useful to reference the graph implementations from the mazes assignment—especially the infinite graphs used in the tests. Notice that these infinite graphs don’t actually store a complete representation of the graph, instead making use of the regular nature of their graphs to lazily generate the output for
neighborswhen the method gets called. This software design pattern reduces the overall memory usage and runtime for large graphs which might otherwise cause Java to run out of memory. The provided
pathFinderfield inDijsktraSeamFindersuggests the graph and edge types for you, but you will need to choose your own vertex object, either by finding a suitable existing type or by writing your own. After choosing a vertex type, you can declare yourGraphsubtype, which should look something like:private class MyGraph implements Graph<MyVertex, Edge<MyVertex>> { // ... }- Make sure to update the
pathFindertype definition afterwards to match your vertex type. - Your graph and any other custom classes must be declared as nested classes within the
DijsktraSeamFinderclass. If you write code in new files, the grader will not be able to find them during grading, which will result in compilation errors. - Don’t name your graph class
Graph, since that will conflict with thegraphs.Graphinterface. - Since horizontal and vertical seams will need slightly different graphs, you may need to create two versions of the graph class or include logic to switch between vertical and horizontal versions of the graph.
Runtime Requirements
- Task
- Make sure that the runtimes for finding seams (in either direction) is in .
Testing
- Recommended
- Read these notes about the testing and grading.
We have not provided many unit tests with this assignment. Instead, we’ve included multiple images of various sizes in the seamcarving/data/ folder, along with the expected energies and seams indicated in text files. Feel free to run the provided demo applications and manually check your results against the expected ones in the text files, or to practice writing your own unit tests.
Submission
- Task
- Commit and push your changes to GitLab before submitting to Gradescope.
After you’re done, remember to complete the individual feedback survey for extra credit, as described on the project main page.
🥳 Congratulations on completing all the assignments!