Experiments

Analyzing the asymptotic behavior of your code.

Table of contents

1. Overview
2. Experiments and Discussion Prompts
   1. Experiment 1: ArrayMap Remove Order
   2. Experiment 2: BinarySearchTreeMap Put Order
   3. Experiment 3: Chaining with Different hashCodes vs. AVL trees
   4. Experiment 4: Load Factor Thresholds for Resizing
   5. Experiment 5: Initial Internal Chain Capacities
3. Submission

Overview

In this part of the assignment, you will run some code that uses the data structures you implemented in the previous part, and then analyze the resulting behavior. This will generally involve the following steps:

1. Read through the experiment methods and make a prediction about their resulting behavior.
2. Run the experiment code and save an image of the resulting plot. (A window displaying the plot should open automatically as the experiment runs.)
3. Answer the discussion questions for each specific experiment in order to explain how or why the experiment produced those results.

The hypothesis/predict-based-on-the-code portions of your write-up will be graded based on completion, so just write down your honest thoughts before running the experiment. Please submit all plots generated along with your answers. The post-experiment analysis portions will be graded based on the clarity of your explanations and whether they match up with your plot.

Your completed write-up must be in PDF format. If you have a partner, you will work on this write-up and submit together.

Warning

If your code from the previous part is buggy, your experiments may produce unexpected results. Make sure you pass all tests on Gradescope before you attempt to analyze any experimental results.

Experiments and Discussion Prompts

Task

For each of the experiments, make a prediction according to the bolded prompt in your write-up before running the experiment or opening its discussion prompts below.
Then, run the experiment, expand the discussion prompts, and answer the questions inside.
Also include the PNGs of the plots inside your write-up PDF.

Include 1–2 sentences of justification for your predictions, and try to keep answers to discussion questions to a maximum of 2–3 sentences.

Experiment 1: ArrayMap Remove Order

This experiment plots the runtime of removing all entries from your array map, but with two different orderings. Read through the code for each test method of the experiment and describe the order that each one removes from the dictionary in terms of the locations of the removed elements in the dictionary’s array. Then, predict the order of growth (constant, logarithmic, linear, $\bm{n\log(n)}$, quadratic, exponential) of each method’s runtime as its size increases.

Experiment 2: BinarySearchTreeMap Put Order

This experiment plots the runtime of adding values to a BST map (sorted based on the keys) with three different key orderings.

Read through each test method, and describe the order that each one adds to the dictionary. Then, predict the order of growth (constant, logarithmic, linear, $\bm{n\log(n)}$, quadratic, exponential) of the runtime of each as its size increases.

Experiment 3: Chaining with Different hashCodes vs. AVL trees

This experiment explores how different hash code functions affect the runtime of a ChainedHashMap, and compare that to the runtime of an AVLTreeMap.

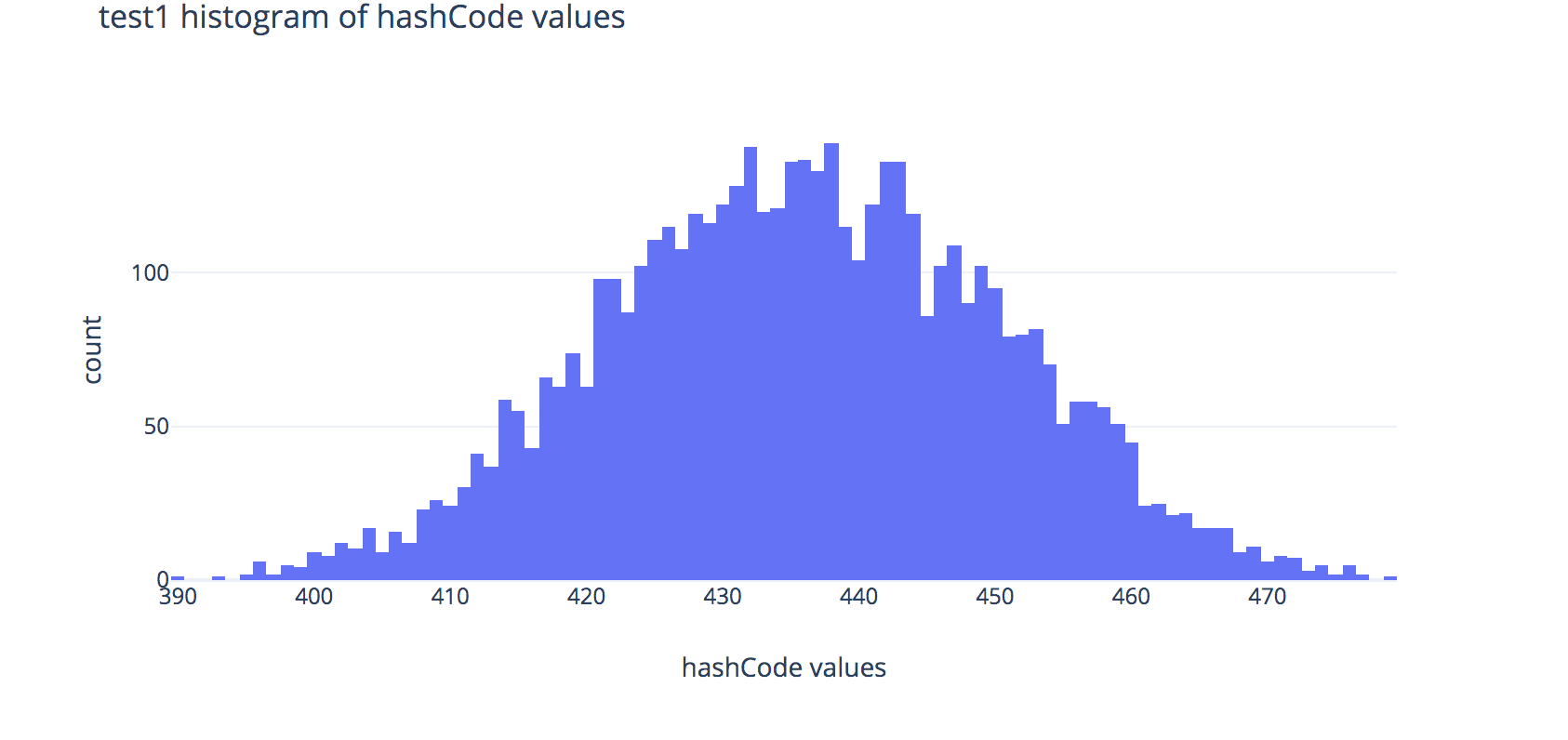
First, we’ll look at the tests involving the ChainedHashMap: test1, test2, and test3. Each uses a different class (FakeString1, FakeString2, and FakeString3 respectively) as keys for a ChainedHashMap. Each of the different fake string objects represent a string (by storing an array of chars) but each class has different implementations of the hashCode method. Read over these implementations of hashCode, and expand the box below to show some plots to help illustrate the output distributions of these hash functions.

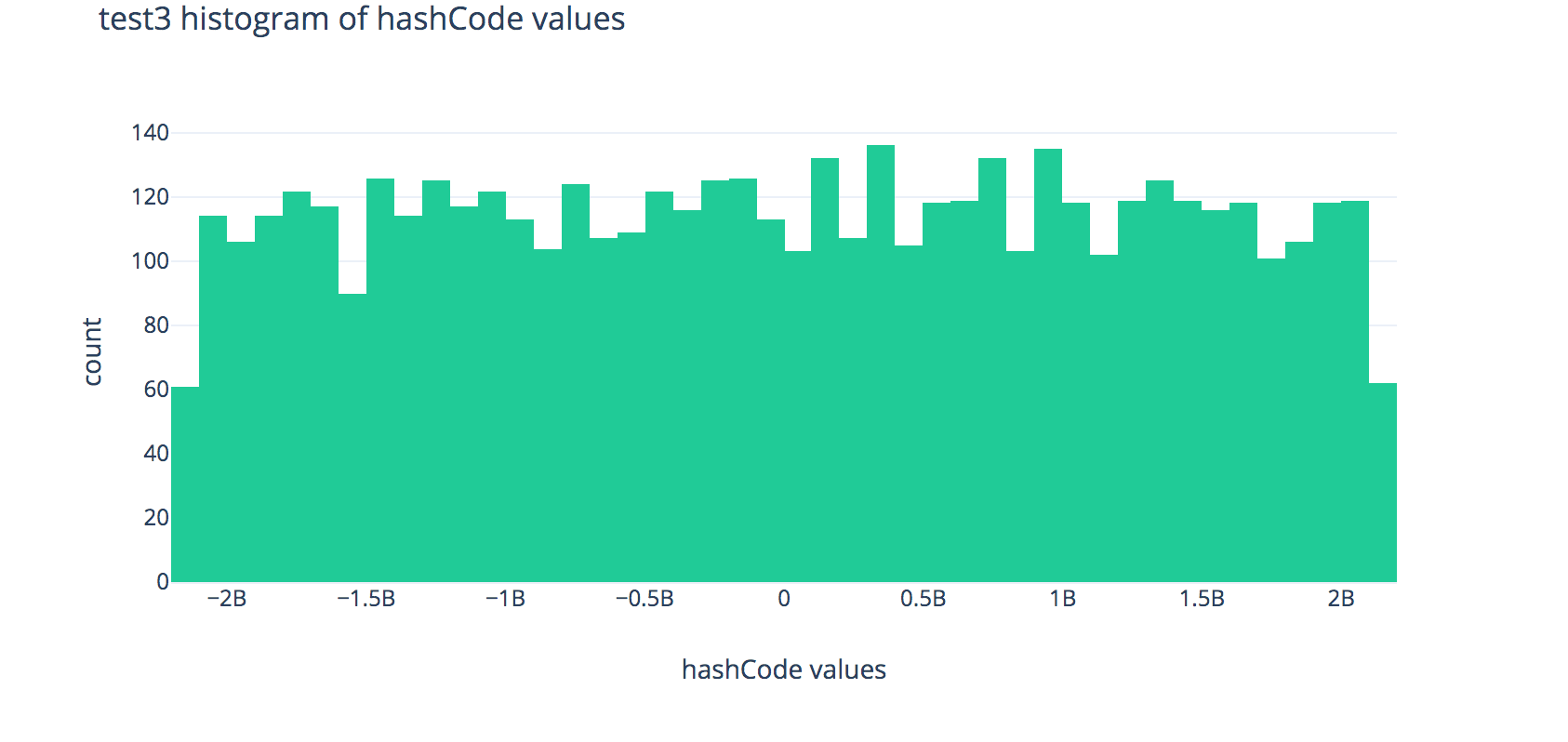
Now, predict which test method will have the fastest and slowest asymptotic runtime growths.

Experiment 4: Load Factor Thresholds for Resizing

This experiment tests the runtime for ChainedHashMap’s put method across different values of the load factor threshold for resizing.

First, answer the following prompts:

1. Briefly describe the difference between test1 and test2.
2. Which test do you expect to run faster? What about asymptotically faster?

Experiment 5: Initial Internal Chain Capacities

This experiment tests the runtime for inserting elements into ChainedHashMap with different initial capacities for the internal ArrayMap chains.

Briefly describe the differences between the three tests.

Submission

Task

Submit your write-up PDF to Gradescope as a group.

When you submit, mark which pages correspond to the questions we ask. After submitting, the partner who uploaded the PDF must add the other partner as a group member on Gradescope. Do not have each member submit individually. The process for adding group members is the same as for the programming portion; if you need a reminder, here’s the video demonstrating the process.

We may deduct points if you do not correctly submit as a group or do not properly assign your pages/problems.

After you’re done, remember to complete the individual feedback survey for extra credit, as described on the project main page.