Programming

Complete the programming portion of the assignment.

Table of contents

1. Deque ADT
2. Debugging ArrayDeque
3. Implementing LinkedDeque
   1. Sentinel Nodes
   2. Invariants
4. Submission

Deque ADT

Background

Understand the ADT you’ll be implementing in this assignment.

Deque (usually pronounced like “deck”) is an irregular acronym of double-ended queue. Double-ended queues are sequence containers with dynamic sizes that can be expanded or contracted on both ends (either its front or its back).¹

Deques can do everything that both stacks and queues can do. Specifically, any deque implementation must have the following operations:

Unlike lists, we do not allow clients to add items to the middle of a deque. We do, however, allow clients to access elements in the deque—this method primarily exists to make it easier for us to test the implementations.

Open the Deque.java file using IntelliJ to explore the interface in more detail. There are a few important things to note here:

• The interface methods defined there include comments with extra notes on edge cases and preconditions.
• Note that this Deque interface extends Java’s Queue interface: this means that it inherits all the methods defined by Java’s Queue interface, and any implementations of this interface must define those methods as well. This is reasonable, since a deque—a double-ended queue—should have strictly more functionality than a queue.
  • In AbstractDeque.java, we define the relationships between our Deque interface and Java’s Queue; this means that subclasses of AbstractDeque can implement the functionality of a deque using our Deque interface, but also provide the functionality of a queue through Java’s Queue interface for free. (Unfortunately, Java does not have a particular interface for stacks, otherwise we would’ve implemented that as well.)
• The rest of this assignment will involve two data structures implementing the deque ADT through our Deque interface. To a client using this code, both implementations should behave the same way, even though the implementations will look drastically different—in fact, this assignment uses essentially the same tests for both implementations.

Debugging ArrayDeque

Task

Fix this buggy Deque implementation.

Explore the Circular ArrayDeque Demo² below to see how the ArrayDeque works: it works similarly to the ArrayQueue class presented in lecture.

We’ve provided a nearly-working ArrayDeque implementation that is intentionally buggy, along with a failing test in BaseDequeTests.confusingTest that causes the bug to emerge. Your task is to fix the flaw in the implementation. (This should only involve changing at most 5 lines of code.)

Follow the debugging cycle:

1. Develop a hypothesis about what the root cause is based on what you know about the problem.
   • Skim through the code in ArrayDeque.java to learn the layout of its methods and fields.
   • Run the provided tests.
   • Read through ArrayDeque again, focusing on methods relevant to the failing tests.
2. Reproduce the issue in a minimal working example.
   • Write and run simple unit tests to help determine what exactly is going wrong. The failing test that we provide isn’t very useful for debugging since it calls many methods—it’s difficult to figure out which of these actually contribute to the test failing, and the number of elements makes it unwieldy to debug. You’ll want to write some simpler tests to figure out what exactly is going wrong.
     • As an aside, it may be useful to write these new tests in BaseDequeTests so that you can later reuse them for LinkedDeque.
   • If you’re having trouble isolating the issue, try using the debugger on your tests to gather additional information that might be difficult or tedious to expose through testing alone.
3. Make productive changes based on the root cause discovered.
   • Make sure that the unit tests you’ve written pass after you’ve fixed the issue.
4. If there are more issues, return to step 1.

Tips

• Don’t try to blindly make changes if you don’t understand how those changes will affect the code. While it’s entirely possible to stumble upon the solution this way, it’s much more likely that this trial-and-error style debugging will “fix” your the problem without addressing the root cause, possibly causing previously-passing tests to start failing.
• Use the Java Visualizer to aid in debugging! It’s very useful for showing the current state of small programs, so write a smaller unit test that causes the bug to emerge, then use the debugger to access the Java Visualizer view.
• For an introduction to IntelliJ’s debugger, check out this presentation from 19sp.
• Do not spend more than an hour debugging! It’s easy to lose track of time and get stuck in a really deep hole when debugging. Please come to office hours, and remember to take breaks! This course is designed to help you learn, but spending too long debugging is not the most efficient way to learn.

• Java’s own stack trace is usually pretty informative. A stack trace shows the history of an exception with the latest method calls on top. For example, the following stack trace shows that an addLast call is responsible for a NullPointerException:

    java.lang.NullPointerException
        at deques.LinkedDeque.addLast(LinkedDeque.java:44)
        at deques.BaseDequeTests.size_afterAddToOppositeEnds_is2(BaseDequeTests.java:126)
  

Implementing LinkedDeque

Task

Implement our Deque interface in LinkedDeque, subject to the following additional requirements:

• add and remove operations must not involve any looping or recursion. A single such operation must take constant time, i.e., execution time should not depend on the size of the deque.
• get must use iteration, not recursion.
• size must take constant time. (This is already implemented for you.)
• The amount of memory that your program uses at any given time must be proportional to the number of items. For example, if you add 10,000 items to the deque, and then remove 9,999 items, the resulting data structure should use memory similar to a deque with 1 item. Do not maintain references to items that are no longer in the deque.
• Your implementation must use sentinel nodes and adhere to the associated invariants.

Sentinel Nodes

Background

Understand sentinel nodes and use them in your implementation.

Sentinel nodes are the solution to one of the age-old problems with linked nodes: handling null references creates code branching that can complicate even the simplest of tasks. The solution is quite simple, too: if we just make sure that a reference is never null, we don’t need to do null checking before accessing its fields!

Of course, to achieve this, we need to assign some non-null value to our references—even when our data structure is empty, any node fields we might access must reference some node. If there’s no data, we’ll need to create a dummy node that doesn’t correspond to any data. And, for simplicity, we may as well keep the dummy node around even when regular data exists; after all, if we special-case the empty case, we defeat the original goal of reducing code complexity.

So, our resulting data structure looks like this³:

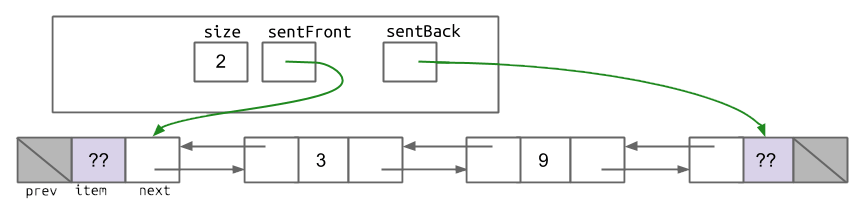
We call these dummy nodes “sentinel nodes” because they always stick around to guard against null pointer exceptions. For more example diagrams and code for sentinel nodes in a singly-linked list, check out this presentation.

Invariants

Background

Understand invariants, and how they are used during grading.

A data structure’s invariants are a set of internal requirements maintained by the data structure: they must be true before and after any of the data structure’s operations. Defining invariants can allow data structure implementers to skip checks for basic assumptions about the data structure: for example, a doubly-linked deque with sentinel nodes should include the following invariants:

• The front field always references the front sentinel node, and the back field always references the back sentinel node.
  • This allows us to skip null checks when access fields of front and back.
• If size is at least 1, front.next and back.prev reference the first and last regular nodes, respectively.
  • This invariant simply defines a property of the data structure in a concrete manner.

Since invariants are always meant to be true in a data structure, we can also explicitly check a data structure’s invariants to determine whether it’s behaving correctly: if an invariant ever becomes false, the data structure must not be implemented correctly.

Our unit tests make extensive use of this: invariant checks will run after the regular assertions of every test to ensure that your deques always remain in a valid state. Here are some other invariants we’ll be checking:

• The nodes in your deque have consistent next and prev fields. For example, if a node curr has a curr.next, we expect to see curr.next.prev == curr.
• The sentinel nodes always have front.prev and back.next referencing null. (These two references should never be accessed during normal deque operations, so them being non-null suggests that something unexpected happened.)

These invariant checks are implemented in the provided tests: the tests in BaseDequeTests call checkInvariants, which for ArrayDeque does nothing, but for LinkedDeque runs the same invariant checking code that we use during grading. (You can find the code in LinkedDequeAssert, if you’re curious.)

There are other linked deque invariants that we could check (e.g., the number of linked nodes corresponds to the size field, the value at each node is correct), but those invariants tend to be easier to test in their own unit tests.

Tips

• If you’re still not sure how to get started, look back at LinkedIntList from project 0. You’re also welcome to refer to LinkedStack.java and LinkedQueue.java from the Algorithms, 4e textbook as case studies. We don’t recommend copying any code from these examples since our approaches aren’t compatible, but the ideas contained within them can be helpful to study.
• Work out what your LinkedDeque will look like on paper before you try implementing them in code! If you can find a willing partner, have them give commands, while you attempt to draw everything out. Try to come up with operations that might reveal problems with your implementation.
• Make sure you think carefully about what happens if the data structure goes from empty, to some non-zero size (e.g. 4 items) back down to zero again, and then back to some non-zero size. This is a common oversight.
• If you find your code failing the grader-only tests on Gradescope, you should try to recreate the test locally so that you can run and debug it. “Get that repro!”
• If your first try goes badly, don’t be afraid to scrap your code and start over. The amount of code for this part isn’t actually that much. (Our solution adds about 40 lines of code to the skeleton.)
• Take things a little at a time. Writing tons of code all at once is going to lead to misery and only misery. Likewise, if you’ve been stuck debugging for more than an hour, take a break and work on something else. It might be particularly helpful to come back later with another perspective.

Submission

Task

Commit and push your changes to GitLab before submitting to Gradescope.

If you’re working in a group, the partner who submits must add the other partner as a group member on Gradescope. Here’s a video demonstrating that process. You’ll also need to re-add group members whenever you resubmit to the same assignment, even if you already did so on a previous submission.

Note

Submitting the same code as another student without using Gradescope’s group feature is considered plagiarism, and may have consequences.

After you’ve made sure that you’re passing all tests on Gradescope, you can start running the experiments.