Description
3D modeling is a key part of the computer graphics and animation pipeline.
This is typically performed using industrial-strength tools like Maya, 3DS Max, and Blender.
These models can be imported to a 3D engine like Unity to create interactions and behaviors that suit your application needs.
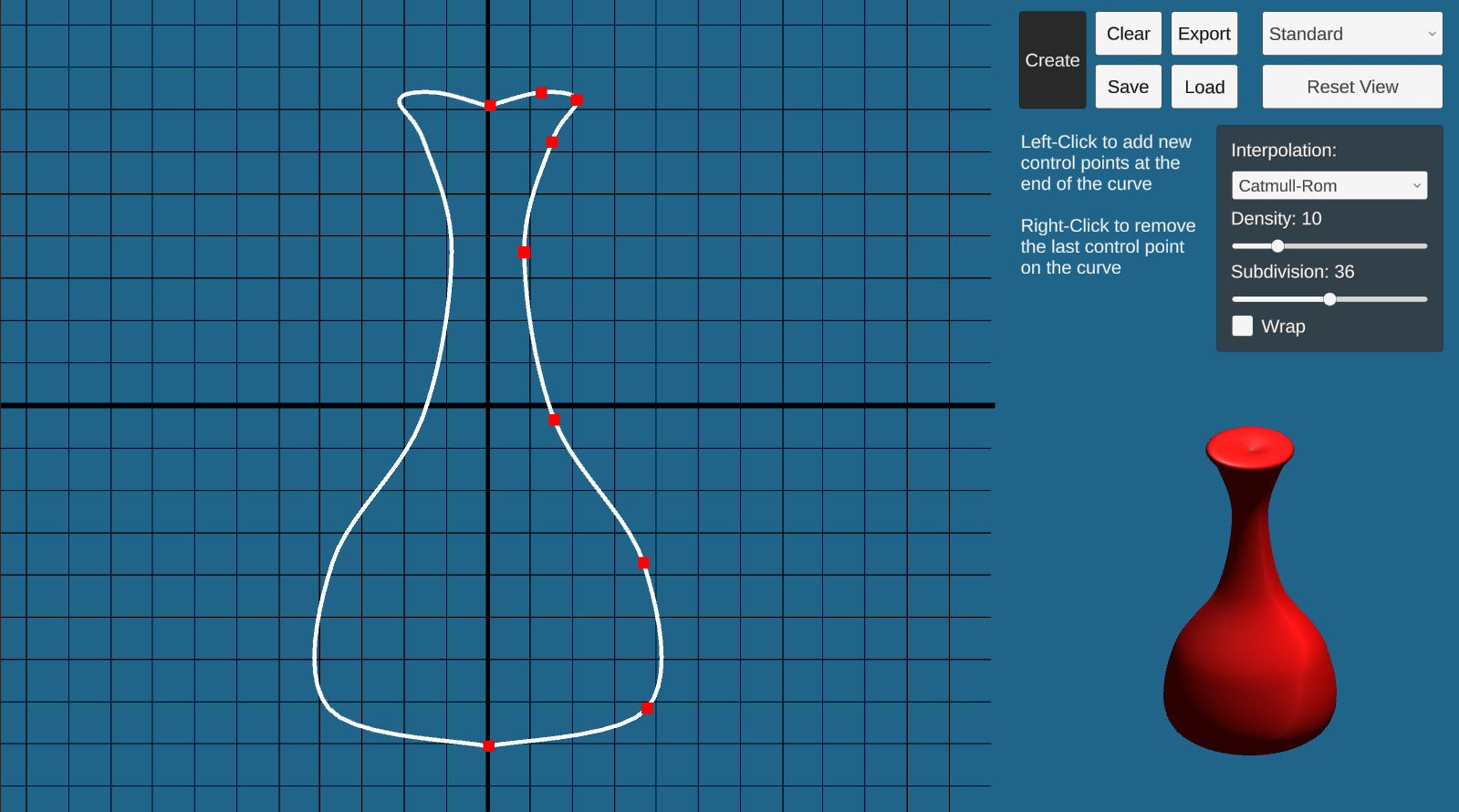
There are three parts to this project. First, you will use the surface of revolution technique to construct a mesh with radial symmetry.
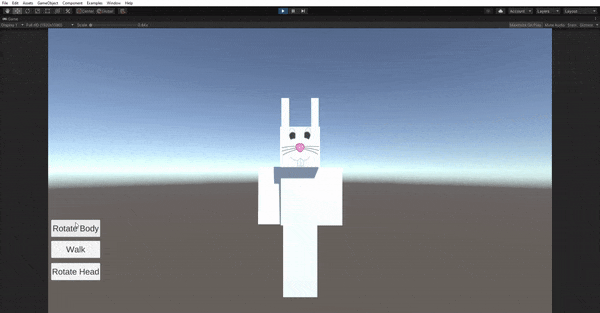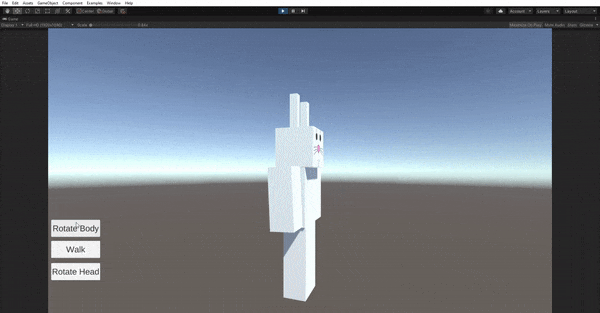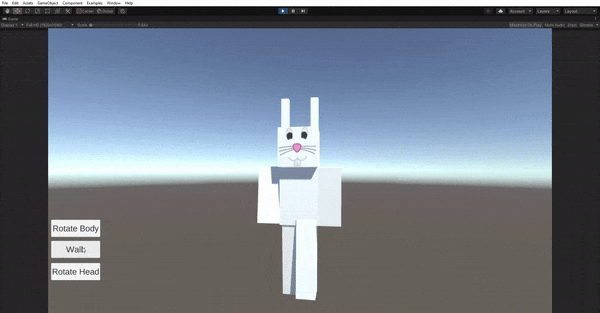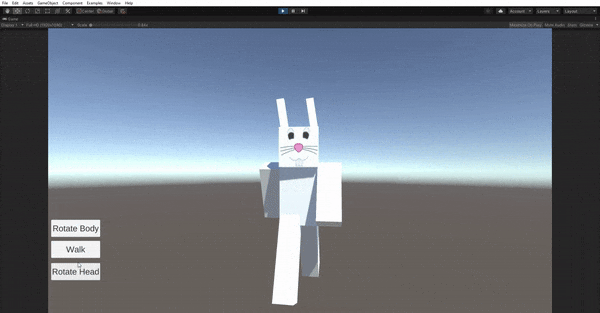
Second, you will compose several geometric primitives using proper hierarchy and transformations to achieve a humanoid model which you
will then create several animation loops for it.
Getting Started
You will need to install Unity to work on this project. For instructions on how to install
Unity and Unity Hub, see the help page.
To open the project, first clone the skeleton code, open Unity Hub, click the Open button and
navigate to your cloned repository. Open the folder that contains the README.md file inside it. It may
take a while the first time opening to import all the necessary packages.
The skeleton code is also avaliable here.
A brief tutorial of Unity is avaliable on the help page.
Implement the surface of revolution in ComputeMeshData() in SurfaceOfRevolution.cs.
You will compute the position, normal, and texture coordinate for each vertex.
The mesh must have correct connectivity (correct vertex orientation and no unnecessary vertices), and you must comply with the number of radial subdivisions.