Projection is the process of creating a two-dimensional image of a three-dimension scene. This process will by necessity discard a great deal of imformation about the actual scene, and so the aim of projection is to convey the sense of the original three-dimensional information in two dimensions.
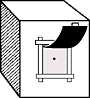
A useful way to understand this process is to use the model of a pinhole camera.

Rays of light enter the camera through a tiny aperature in front. They strike a photographic plate at the back of the camera. The result is that an inverted image of the view from the aperature is captured in the plate.
By reducing the hole to an ideal point, we can describe the pinhole camera mathematically:

The point (x,y,z) represents the origin of some light ray that enters the camera and strikes the photographic plate. Using the fact that the two triangles in the diagram are similar, we can derive the position of the image of the point on the plate:
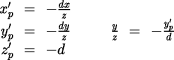
In homogeneous coordinates, we can express this relationship as
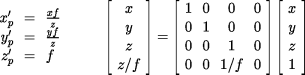
Of course, to turn this inverted image into a true representation of the original scene, it is necessary to pass the image 'back through' the aperature and project it onto another plate. This is how modern cameras operate; the image captured on film is a negative, which has both colour and position inverted. The negative is used to produce a true reproduction of the scene.
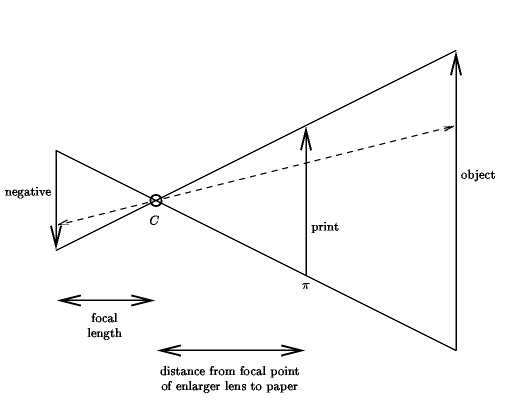
Because we are simulating this process, there is no need to include the extra step of producing the negative. We can project directly onto an imginanary piece of glass placed between the eye and the scene. This is in fact how renaissance artists originally conceived of the laws of perspective. They began to see a painting as the exact configuration of light rays striking an imaginary (or real!) piece of glass, rather than as a stylized description of their perception of a scene.
 Previous: Elementary Transformations |
 Up: Geometric Transformation Index |
 Next: Types of Projection |