
Project 2 : Modeler
Assigned: Thursday, April 14th
Due: Thursday, April 28th by 11:59pm
Artifact Due: Monday, May 2nd by 11:59pm
Help Sessions (Graphics lab, Sieg 327):
Friday April 15th, 12:30 to 1:15 PM
Tuesday April 19th, 3:30 to 4:30 PM
Project TA: Jeff Booth
Groups
Quick Links
- Sample Solution (can also be found in your repository).
- ">Installer for FLTK if you're working from home.
- ">FLTK source code if you want to build FLTK yourself.
- Sample executables (also check out the winners from previous quarters linked below)
- Official OpenGL documentation
- Some great OpenGL tutorials
- Help Session Slides: PowerPoint 2007 format (tiny) and PDF format (BIG!)
Examples of Past Models
Getting Started
To get going, you need to get the skeleton source code. This is distributed via SVN, which is all set up for you. In the labs, we will be using TortoiseSVN. In order to get the source code, follow the directions below:
Graphics Lab:
- Create a new folder somewhere (such as your Z: drive) with the name 'modeler', right click on it, and choose 'SVN Checkout'
- In the 'URL of repository' field, enter:
file://\\ntdfs/cs/unix/projects/instr//cse457/modeler/YOUR_ASSIGNED_GROUP_NAME/source
When copying this string (then editing the group name), be careful that the
"\"s and "/"s are preserved exactly as they appear on this page.
- Make sure that the 'HEAD revision' radio button is selected, and hit OK
- A working copy of the source code will be checked out into the folder. You're now ready to work!
Remote Access:
- Make sure you have FLTK 1.1.10 installed on your computer. If you're running Windows and using Microsoft Visual Studio 2010 Express Edition, then you can download and run the FLTK Installer. Otherwise, you'll need to download and compile the FLTK source code.
- One way to access your repository is to use TortoiseSVN. Download it here.
- Then, the link to your repository would be:
svn+ssh://YOUR_CSE_NET_ID@attu.cs.washington.edu/projects/instr//cse457/modeler/YOUR_ASSIGNED_GROUP_NAME/source
If you plan to work from home, you will either need to use the FLTK Installer or point Visual Studio to the correct include and library directories for the FLTK that came in your repository (since normally it points to the local one on each lab machine). Instructions for how to do this. To open and build the project, double-click modeler.vcxproj.
Part 1: Rendering a Sphere
In OpenGL, all scenes are made of primitives like points, lines, triangles and quadrilaterals. Only the following primitives create triangles and quadrilaterals, which can be used to make 3D surfaces:
- GL_TRIANGLES
- GL_TRIANGLE_STRIP
- GL_TRIANGLE_FAN
- GL_QUADS
- GL_QUAD_STRIP
For each primitive, you send a list of vertices, which are the points that make up the primitive. The resulting shape depends on the primitive you chose. To send a vertex to the graphics hardware, you call glVertex3f(x, y, z). Here's an example that draws a 3D square:
glBegin(GL_QUADS);
glVertex3f(0, 0, 0);
glVertex3f(1, 0, 0);
glVertex3f(1, 1, 0);
glVertex3f(0, 1, 0);
glEnd();
You can read more about OpenGL's primitives here.
However, these primitive aren't very sophisticated building blocks for scenes. So we'll invent more interesting primitives.
Your Task:
Write code to draw your own sphere primitive in the drawSphere() method in modelerdraw.cpp. Your sphere must:
- have appropriate texture coordinates for each vertex
- have appropriate per-vertex normals
- have surfaces drawn using only OpenGL library calls (not calls to drawSphere(), or to GLU or GLUT as the drawSphere() method currently does.)
- use the divisions variable that already exists in drawSphere()
to determine how many rings your sphere is sliced into vertically, and
how many slices each ring is divided into.
- be displayed in your final scene for grading. If you don't want the required shape to be part of your final scene, create a switch to turn it on or off by using a BooleanProperty in your model or scene.
Using Textures In Your Model
When you want to use a texture, you'll need to do the following:
- Add a Texture2D field to your model class
- In your model class's load() method, call the field's load() method
class MyModel : public Model {
Texture2D checkers;
public:
// Constructor for MyModel
MyModel() :
checkers("checkers.png")
{
}
// Your load method
void load() {
checkers.load();
}
// Your draw method
void draw() {
// all geometry after this point will have the checkers texture
checkers.use();
}
};
If you want to get the texture's ID for more advanced stuff:
GLuint textureID = texture.getID();
If you want to use another texture, just call that texture object's
use() method. To stop using textures, call:
glBindTexture(0);
Texture Mapping
Texture mapping allows you to "wrap" images around your model by mapping points on an image (called a texture) to vertices on your model. For each vertex, you indicate the coordinate that vertex should apply to, using the command glTexCoord2f(s, t), where s is the X-coordinate and t is the Y-coordinate of the point on the texture that should line up with the vertex. You call glTexCoord2f() right before the vertex you want to apply it to:
texture.use();
glBegin(GL_TRIANGLES);
...
glTexCoord2f(0, 0);
glVertex3f(0, 0, 0);
...
glEnd();
glBindTexture(0);
Surface Normals
Surface normals are perpendicular to the plane that's tangent to a surface at a given vertex. Surface normals are used for lighting calculations, because they help determine how light reflects off of a surface. Each normal is sent by calling glNormal3f(x, y, z) before the call to glVertex3f(), much like texture mapping.
In OpenGL, we often want to approximate smooth shapes like spheres and cylinders
using only triangles and quadrilaterals. One way to make the lighting look smooth is to use the normals from the shape we're trying to approximate, rather than just making them perpendicular to the polygons we draw. This means we calculate the normals for each vertex (per-vertex normals), rather than each face (per-face) normals. Shaders allow us to get even smoother lighting, calculating the normals at each pixel. You can compare these methods below:

In your sphere, you will need to use this trick: calculate your normals from the shape you're trying to model, rather than the polygons you're using to model it.
Part 2: The Hierarchical Model
A hierarchical model is a way of grouping together shapes and attributes to form a complex object. Parts of the object are positioned relative to each other instead of the world. Think of each object as a tree, with nodes decreasing in complexity as you move from root to leaf. Each
node can be treated as a single object, so that when you modify a node you end up modifying all its children together. Hierarchical modeling is a very common way
to structure 3D scenes and objects, and is found in many other contexts. If hierarchical modeling is unclear to you, you are encouraged to look at the Hierarchical Modeling lecture notes.
Your Task:
You must come up with a character that meets these requirements:
- Uses glTranslate(), glRotate(), and glScale() in meaningful ways.
- Has at least two levels of branching - There must be at least two instances in your model where you draw something, save the current matrix, apply an affine transformation such as glTranslate(), glRotate() or glScale(), draw something else, then return to your previous matrix, apply a new transformation, and draw something else. You must also use glPushMatrix() and glPopMatrix() to nest your matrix transformations (see below for details). Here's a pseudocode example of a minimal solution, along with a scene graph:
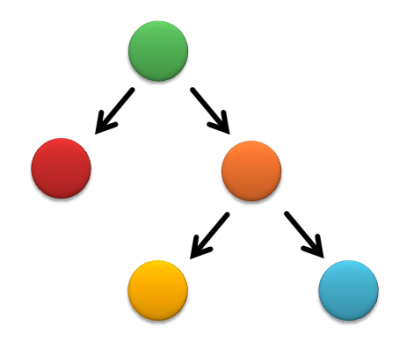
draw geometry
push matrix
translate up
draw geometry
push matrix
translate left
draw geometry
pop matrix
push matrix
translate right
draw geometry
pop matrix
pop matrix
push matrix
translate down
draw geometry
pop matrix
- Has at least 1 multiple-joint slider that controls multiple joints or components of your model. For example, you might have your character waving, which would require that you control the shoulder and elbow joints simultaneously.
Making a Model
You will want to make a model to draw your character, by extending the Model class in model.h:
class MyModel : public Model {
public:
// Constructor for MyModel
MyModel() {
}
// Draws the model onscreen
void draw() {
// ... call your drawing functions here ...
}
};
The easiest way to get started is to just modify the existing Scene class in sample.cpp.
It extends Model, and in the main() method at the bottom, an instance of it is given to
ModelerUserInterface to be displayed onscreen. Later on, you can create your own Model
subclass and add it to the Scene class, much like the PointLight and DirectionalLight
Models are added. See sample.cpp for details.
Adding Properties To Your Model
A property is an aspect of your model that the user can control. Modeler represents different types of properties with Property classes in model.h:

|
RangeProperty stores a single number that's within a continuous range.
|

|
RGBProperty stores a color's red, green, and blue components. Modeler lets you set it with a color picker.
|

|
BooleanProperty is either true or false. Modeler lets you set it with a checkbox, making it useful for showing or hiding parts of your model.
|
|
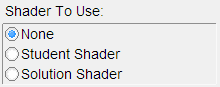
ChoiceProperty has an integer value from 0 to N - 1, where N is the number of choices it has. You can assign names to each choice, and Modeler will show the names in the control panel.
|
To add a property to your model class, do the following:
class MyModel : public Model {
Make sure protected: comes before properties, unless you want to be able to access them from other classes (in that case, use public:).
protected:
Add the property here:
RangeProperty height;
public:
MyModel() :
put constructor here, after the above colon
height("Height", 0.0f, 10.0f, 0.0f, 0.1f)
{
Add the property to the model's GroupProperty, which is a group of properties that's a property of every Model.
properties.add(&height);
}
void draw() {
Use your new property's value for something:
glScalef(0, height.getValue(), 0);
}
};
Now, when you open Modeler, a control for your property appears on the left panel.

For further details on each property class, look in model.h. To see how they are added to models, look at the skeleton code's sample model in sample.cpp.
WARNING: If you try to set the value of a property of your model
by calling setValue(), setRed(), etc., the slider, color picker, or checkbox corresponding
to that property will not be updated to show that property's new value. This problem is
an oversight in the design of the new Modeler, but will not prevent you from completing
the project requirements. If you find yourself needing to set your model's properties,
consult your TA's, because you might not be using the Model class the way it was intended to
be used.
Affine Transformations in OpenGL
The graphics primitives you have (box, sphere, and cylinder) only accept parameters that define their dimensions. That means you can draw a box, sphere, or cylinder of any size, but it will always be at the origin with the same orientation. What if you want to move it somewhere else, or rotate it to a different orientation -- and you can't edit the primitive's drawing code?
In OpenGL, every vertex is multipled by the modelview matrix, then by the projection matrix:
- Modelview Matrix - transforms a point into eye / camera space, where the camera's eye is at the origin, looking down the -z axis, with its up-vector aligned with the +y axis.
- Projection Matrix - transforms a point from eye / camera space into normalized device space, which is a 2D plane that represents your screen surface. Its coordinates go from -1 to 1 on each axis, and conversion to pixels is done depending on the size of your OpenGL window.
Since Modeler takes care of projection, you'll modify the modelview matrix. OpenGL has several functions that create matrices for common transformations, then multiply them by the modelview matrix:
- glRotatef(degrees, x, y, z) - Rotates all vertices by degrees degrees around a line with slope vector <x, y, z> that passes through the origin. Use the right-hand rule with the vector to determine the direction of rotation.
- glTranslatef(x, y, z) - Add <x, y, z> to all vertices.
- glScalef(x, y, z) - Multiplies all vertices by <x, y, z>, producing a scaling effect relative to the origin.
If you called glTranslatef(1, 0, 0), then called drawSphere(1), the sphere would be drawn centered around (1, 0, 0) because all of its vertices had 1 added to their X-coordinates. Each transformation has the effect of creating a "model space" with its own origin and axes. The sphere was drawn at the origin of a model space created by glTranslatef(1, 0, 0).
Hierarchical Transformations in OpenGL
Once you have applied a transformation to the modelview matrix, it will be applied to EVERY point sent to the graphics card forever! To undo the transformation, you need to remember the matrix's contents.
- Use the glPushMatrix() function to push the current modelview matrix onto OpenGL's internal stack.
- Then, use glPopMatrix() to pop the last pushed matrix off that stack and copy it into the modelview matrix.
Make sure you match each glPushMatrix() with a corresponding glPopMatrix(), so that your modelview matrix is returned to its original state. This makes it easy to "nest" your transformations:
// Here, modelview matrix is in world space
glPushMatrix(); // save world space matrix
// Still in world space
glTranslate(1, 0, 0);
// Now in model space (everything translated left by 1).
drawSphere(1);
// Here's a "nested" transformation. After the corresponding glPopMatrix(),
// we'll be back in model space.
glPushMatrix(); // save model space matrix
// Still in model space
glTranslate(3, 0, 0)
// Now in "model space 2"
drawSphere(1);
glPopMatrix(); // copy model space matrix into modelview matrix
// Back in model space
glPopMatrix(); // copy world space matrix into modelview matrix
// Back in world space
Part 3: gluLookAt
In 3D graphics, it's convenient to define a camera by indicating three vectors:
- Eye position - the position of the camera's "eye" in world space.
- Look-at point - a point in world space that the camera is looking at.
- Up-vector - a vector in world space that indicates which direction is "up".
Unfortunately, in OpenGL, the camera is stuck at the origin, looking down the -z axis, with its up-vector aligned with the y axis. When the camera is here, we're in camera space. The camera must be here for projection to work properly, so we can't move the camera. Instead, we can create an affine transformation between world and camera space.
OpenGL contains a utility function called gluLookAt(), which takes these three vectors and creates an affine transformation that "moves" the entire scene such that the camera ends up at the origin, looking down the negative Z-axis, with its up-vector pointing along the positive Y-axis. It applies this transformation to the modelview matrix, so that the transformation gets applied to all subsequent vertices. The Camera class (camera.cpp) contains a method applyViewingTransform(), which uses gluLookAt() for the Modeler camera.
Your Task:
Replace the call to gluLookAt() in camera.cpp with your own code. You may choose to do this using glTranslate()s and glRotate()s. Or, even better, you can build the matrix yourself and use glMultMatrix() to apply the transformation.
- You are encouraged to look at the documentation of gluLookAt() yourself. Hint: check out the blue openGL book that is floating around the labs.
- When working on this part of the project, please take advantage of the vector and the matrix classes found in vec.h and mat.h (but not vect.h). The vector class can perform both dot products and cross products using the "*" and "^" operators respectively. Both the vector class and matrix class have many useful features that will make your work here much easier.
- A good place to start for this is the Angel text in sections 5.3.2 and 5.3.3.
Part 4: Point Light Blinn-Phong Shader
A shader is a program that controls the behavior of a piece of the graphics pipeline on your graphics card.
- Geometry shaders can turn a single point into multiple points. They are useful for
advanced modeling, e.g., refining a coarse triangle mesh into a smooth surface
with many triangles, but require very recent graphics hardware and are not
part of the core requirements of this project.
- Vertex shaders are run once for each vertex in your model. They transform it into device space (by applying the modelview and projection matrices), and determine what each vertex's properties are.
- Fragment (or pixel) shaders are run once for every pixel to determine its color.
Shaders determine how the scene lighting affects the coloring of 3D surfaces. In OpenGL,
there are two basic kinds of lights:
- Point Light - a light that is emitted from a point in world space. The intensity of the light is attenuated (reduced) based on how far it travels from this point. In the physical world, the intensity of a point light decreases with the square of the distance. We can model this with quadratic distance attenuation: dividing the intensity by some function a*r^2+b*r+c, where r is the distance from the light source and a, b, and c are chosen arbitrarily.
- Directional Light - a light that always hits a surface from a certain direction, no matter where it is. It has no attenuation.
A shading model determines how the final color of a surface is calculated from a scene's light sources and the object's material. We have provided a shader that uses the Blinn-Phong shading model for scenes with directional lights. See lecture notes for details on the Blinn-Phong shading model.
Your Task:
Add support for the scene's point light, by editing the files shader.vert and shader.frag. You need to include quadratic distance attenuation. Please open these files and read the comments for details.
- gl_LightSource[1].position stores the point light's position.
- gl_FrontLightProduct[1] is a structure that contains the material properties of the object (ambient, specular, and diffuse colors) multiplied by the point light's ambient, specular and diffuse colors.
- You can visit this site for a helpful tutorial with code included!
- Hint: you may not have to edit one of the files.
We have provided the sample solution modeler_solution.exe in your repository, which lets you compare your shader to the (correct) sample solution shader. To choose which shader to show, click on "Scene" and click the radio button for the shader you want to use. The sample solution also contains both a point light and a directional light for you to manipulate. Click the "Point Light" or "Directional Light" on the list in the top left corner to edit a light's properties or move it around.
Part 5: Yet Another Shader
Your Task:
Create another shader that is worth at least 1 whistle on the chart below. Any additional bells or whistles will be extra credit. You must keep your
point light Blinn-Phong shader from Part 4 separate, so we can grade it separately, and you must exhibit this shader in your Modeler binary. Consult the OpenGL orange book for some excellent tips on shaders. Ask your TA's if you would like to implement a shader that isn't listed below. Credit for any shader may be adjusted depending on the quality of the implementation, but any reasonable effort should at least earn you the required whistle.
 Spot Light Shader - Create a shader that supports a spot light source, and add a third light source to your Modeler. We should be able to adjust the spot light parameters via sliders.
Spot Light Shader - Create a shader that supports a spot light source, and add a third light source to your Modeler. We should be able to adjust the spot light parameters via sliders.
 Cartoon Shader - Create a shader that produces a cartoon effect by drawing a limited set of colors.
Cartoon Shader - Create a shader that produces a cartoon effect by drawing a limited set of colors.
 Blinn-Phong and Texture Mapping Shader - Extend your Blinn-Phong shader to support texture mapping. Remember to keep a copy of your original Blinn-Phong shader for grading.
Blinn-Phong and Texture Mapping Shader - Extend your Blinn-Phong shader to support texture mapping. Remember to keep a copy of your original Blinn-Phong shader for grading.
 Tessellated Procedural Shader - Make a shader that produces an interesting, repeating pattern, such as a brick pattern, without using a texture.
Tessellated Procedural Shader - Make a shader that produces an interesting, repeating pattern, such as a brick pattern, without using a texture.
 Bump Mapping Shader - This shader uses a texture to perturb the surface normals of a surface to create the illusion of tiny bumps, without introducing additional geometry.
Bump Mapping Shader - This shader uses a texture to perturb the surface normals of a surface to create the illusion of tiny bumps, without introducing additional geometry.

 Environment Mapped Shader - To make an object appear really shiny (i.e. metallic), it needs to reflect the objects around it. One way to do this is to take a panoramic picture of the surroundings, store it in a texture, and use that texture to determine what should be reflected. For simplicity, we recommend obtaining an existing environment map from somewhere (perhaps making it yourself with a 3D raytracer).
Environment Mapped Shader - To make an object appear really shiny (i.e. metallic), it needs to reflect the objects around it. One way to do this is to take a panoramic picture of the surroundings, store it in a texture, and use that texture to determine what should be reflected. For simplicity, we recommend obtaining an existing environment map from somewhere (perhaps making it yourself with a 3D raytracer).

 Cloud / Noise Shader - Create a shader that uses noise functions (like Perlin noise) to generate clouds. You may not use textures for this shader. Credit depends on the realism of the clouds.
Cloud / Noise Shader - Create a shader that uses noise functions (like Perlin noise) to generate clouds. You may not use textures for this shader. Credit depends on the realism of the clouds.
You can use the sample solution Modeler to develop some of these shaders, but others require texture maps to be provided -- which the sample solution may not provide to your shader.
Using Shaders In Your Model
Shader files are loaded, compiled, and linked by ShaderProgram objects.
If you want to add a shader:
- Add a ShaderProgram field to your model.
- Call its constructor after the colon for your model's constructor.
The ShaderProgram constructor takes three filenames:
- Vertex shader
- Pixel shader
- Geometry shader (omit this parameter unless you actually have one)
class MyModel : public Model {
public:
Texture2D texture;
ShaderProgram shader;
// Your model constructor
MyModel() : // after this colon go the constructors for your shaders,
// textures, and properties:
texture("checkers.png"),
shader("shader.vert", "shader.frag")
{}
};
If you have an error in your shader code, YOU DON'T HAVE TO RESTART MODELER! Instead,
fix your shader, then go to File->Reload Textures And Shaders.
Now, if you made a ShaderProgram field called shader, you could use that
shader in your draw() method like this:
shader.use();
This shader will be applied to all subsequent geometry.
If you want to use another shader, just call that shader object's
use() method. To stop using shaders, call:
glUseProgram(0);
If you want to get the shader program's ID for more advanced stuff:
GLuint shaderProgramID = shader.getID();
NOTE: Like the rest of your Modeler binary, your shaders must work on the lab machines. If your code complies with the GLSL standard, it should work fine. One way you can verify that your code is compliant with the GLSL standard is to install the
GLSL Validator tool.
However, please still test on the lab machines if possible.
Turn-In Procedure
By the deadline, you will need to upload the following deliverables
to your group's folder. For details on accessing this folder, from
the lab or at home,
visit the Turn-In Instructions.
Source Folder
Please copy all the source code needed to build your project into the turnin/source folder. DO NOT copy the Debug or Release folders here.
Binary Folder
- Build your program in Release mode by choosing "Release" in the dropdown menu next to the play button at the top of the Visual Studio screen, then pressing F7 to build:
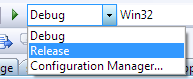
- Copy modeler.exe from the Release folder of your project.
- Copy your Part 4 shader files, which should be named "shader.frag" and "shader.vert" so we can load them into the sample solution and compare. You may name your other shaders as you like, but we recommend that the fragment shaders end in .frag and the vertex shaders end in .vert.
- Also copy all of your shaders, textures, and other files needed to run your program -- you should be able to run it right out of the turnin/binary folder.
Artifact Submission
The modeler application itself is the artifact. To submit it, you will need to do a few special steps you didn't need to do for the binary submission. Basically, you'll encrypt your Modeler shaders and embed them in your program.
You will turn in one artifact per group
- Make sure your shaders are compliant with the GLSL standard, by checking them with the GLSL Validator tool. Otherwise, some people might not be able to run your artifact.
- Build your Modeler application in Debug mode.
- Run your Modeler application. On its File menu, click Generate shaders.cpp. This will bundle all your shaders into a file named shaders.cpp, which was previously empty. It also encrypts your shaders, making it more difficult for future students to steal your hard work.
- Recompile your application in Release mode. This will cause shaders.cpp to be included in your binary, and in Release mode, the Generate shaders.cpp menu option will be hidden. If you don't compile in Release mode, many people may not be able to run your artifact. Also, we may take down your submission at the end of the quarter (since future students could generate their shaders.cpp files from your submission).
- Create a zip file containing only your Modeler application, its textures, and any other files it needs to run. Do not include shaders, as they were "built into" your Modeler binary file when you compiled it with shaders.cpp.
- Extract your zip file to your desktop, and make sure that you can run Modeler (i.e. you aren't missing any files, and the most recent versions of your shaders are being used).
- Take a screenshot using File->Save Image... from inside your app.
- Turn in your screenshot, zip file, and any comments or directions on how to use your Modeler here.
NOTE: If Modeler generates a broken shaders.cpp file, you can undo the change by replacing the contents of shaders.cpp with:
#include "vault.h"
const char* SHADER_KEY = NULL;
int SHADER_COUNT = 0;
const char* SHADER_FILENAMES[1];
const char* SHADER_DATA[1];
Extra Credit: Bells and Whistles
Two whistles are worth one bell, and one bell is worth one point on the project.
 Come up with another whistle and implement it. A whistle is something that extends the use of one of the things you are already doing. It is part of the basic model construction, but extended or cloned and modified in an interesting way. Ask your TAs to make sure this whistle is valid.
Come up with another whistle and implement it. A whistle is something that extends the use of one of the things you are already doing. It is part of the basic model construction, but extended or cloned and modified in an interesting way. Ask your TAs to make sure this whistle is valid.
 Build a complex shape as a set of polygonal faces, using triangles (either the provided primitive or straight OpenGL triangles) to render it.
Examples of things that don't count as complex: a pentagon, a square, a circle. Examples of what does count: dodecahedron, 2D function plot (z = sin(x2 + y)), etc.
Build a complex shape as a set of polygonal faces, using triangles (either the provided primitive or straight OpenGL triangles) to render it.
Examples of things that don't count as complex: a pentagon, a square, a circle. Examples of what does count: dodecahedron, 2D function plot (z = sin(x2 + y)), etc.
 On the Modeler menu bar, there is an Animate menu. When you click it and check the "Enable" box, your model's tick() method will get called about 24 times per second, and its draw() method will be called at least that often. The rate is controlled by the variable framesPerSecond in modelerui.cpp. You can use this fact to implement an animation. You can keep track of time by incrementing a counter every time your tick() method is called.
On the Modeler menu bar, there is an Animate menu. When you click it and check the "Enable" box, your model's tick() method will get called about 24 times per second, and its draw() method will be called at least that often. The rate is controlled by the variable framesPerSecond in modelerui.cpp. You can use this fact to implement an animation. You can keep track of time by incrementing a counter every time your tick() method is called.
 Add some widgets that control adjustable parameters to your model so that you can create individual-looking instances of your character.
Try to make these actually different individuals, not just "the red guy" and "the blue guy."
Add some widgets that control adjustable parameters to your model so that you can create individual-looking instances of your character.
Try to make these actually different individuals, not just "the red guy" and "the blue guy."
 A display list is a "recording" of OpenGL calls that gets stored on the graphics card. Thus, display lists allow you to render complicated polygons much more quickly because you only have to tell the graphics card to replay the list of commands instead of sending them across the (slow) computer bus. A display list tutorial can be found here.
A display list is a "recording" of OpenGL calls that gets stored on the graphics card. Thus, display lists allow you to render complicated polygons much more quickly because you only have to tell the graphics card to replay the list of commands instead of sending them across the (slow) computer bus. A display list tutorial can be found here.
 Implement a smooth curve functionality. Examples of smooth curves are here.
These curves are a great way to lead into swept surfaces (see below). Functional curves will need to be demonstrated in some way. One great example would be to draw some polynomial across a curve that you define.
Students who implement swept surfaces will not be given a bell for smooth curves. That bell will be included in the swept surfaces bell. Smooth curves will be an important part of the animator project, so this will give you a leg up on that.
Implement a smooth curve functionality. Examples of smooth curves are here.
These curves are a great way to lead into swept surfaces (see below). Functional curves will need to be demonstrated in some way. One great example would be to draw some polynomial across a curve that you define.
Students who implement swept surfaces will not be given a bell for smooth curves. That bell will be included in the swept surfaces bell. Smooth curves will be an important part of the animator project, so this will give you a leg up on that.
 Implement one or more non-linear transformations applied to a triangle mesh. This entails creating at least one function that is applied across a mesh with specified parameters. For example, you could generate a triangulated sphere and apply a function to a sphere at a specified point that modifies the mesh based on the distance of each point from a given axis or origin. Credit varies depending on the complexity of the transformation(s) and/or whether you provide user controls (e.g., sliders) to modify parameters.
Implement one or more non-linear transformations applied to a triangle mesh. This entails creating at least one function that is applied across a mesh with specified parameters. For example, you could generate a triangulated sphere and apply a function to a sphere at a specified point that modifies the mesh based on the distance of each point from a given axis or origin. Credit varies depending on the complexity of the transformation(s) and/or whether you provide user controls (e.g., sliders) to modify parameters.
 Implement the "Hitchcock Effect" described in class, where the camera zooms in on an object, whilst at the same time pulling away from it (the effect can also be reversed--zoom out and pull in).
The transformation should fix one plane in the scene--show this plane. Make sure that the effect is dramatic--adding an interesting background will help, otherwise it can be really difficult to tell if it's being done correctly.
Implement the "Hitchcock Effect" described in class, where the camera zooms in on an object, whilst at the same time pulling away from it (the effect can also be reversed--zoom out and pull in).
The transformation should fix one plane in the scene--show this plane. Make sure that the effect is dramatic--adding an interesting background will help, otherwise it can be really difficult to tell if it's being done correctly.
 Heightfields are great ways to build complicated looking maps and terrains pretty easily.
Heightfields are great ways to build complicated looking maps and terrains pretty easily.

 Add a function in your model file for drawing a new type of primitive. The following examples will definitely garner two bells; if you come up with your own primitive, you will be awarded one or two bells based on its coolness.
Here are three examples:
Add a function in your model file for drawing a new type of primitive. The following examples will definitely garner two bells; if you come up with your own primitive, you will be awarded one or two bells based on its coolness.
Here are three examples:
- Surfaces of rotation - given a curve and an axis, draw the surface that results from sweeping the curve around the axis. This is really nice for making pottery :).
- Rail surfaces - see Watt, p. 41.
- Swept surfaces (this is worth 3 bells) -- given two curves, sweep one profile curve along the path defined by the other. These are also known as "generalized cylinders" when the profile curve is closed.
This isn't quite as simple as it may first sound, as it requires the profile curve to change its orientation as it sweeps over the path curve. See this page for some uses of generalized cylinders.
This document
may be helpful as well, or see the parametric surfaces lecture from a
previous offering of this class.

 (Variable) Use some sort of procedural modeling (such as an L-system) to generate all or part of your character.
Have parameters of the procedural modeler controllable by the user via control widgets.
In a previous quarter, one group generated these awesome results.
(Variable) Use some sort of procedural modeling (such as an L-system) to generate all or part of your character.
Have parameters of the procedural modeler controllable by the user via control widgets.
In a previous quarter, one group generated these awesome results.

 In addition to mood cycling, have your character react differently to UI controls depending on what mood they are in.
Again, there is some weight in this item because the character reactions are supposed to make sense in a story telling way.
Think about the mood that the character is in, think about the things that you might want the character to do, and then provide a means for expressing and controlling those actions.
In addition to mood cycling, have your character react differently to UI controls depending on what mood they are in.
Again, there is some weight in this item because the character reactions are supposed to make sense in a story telling way.
Think about the mood that the character is in, think about the things that you might want the character to do, and then provide a means for expressing and controlling those actions.


 One difficulty with hierarchical modeling using primitives is the difficulty of building "organic" shapes.
It's difficult, for instance, to make a convincing looking human arm because you can't really show the bending of the skin and bulging of the muscle using cylinders and spheres.
There has, however, been success in building organic shapes using metaballs.
Implement your hierarchical model and "skin" it with metaballs. Hint: look up "marching cubes" and "marching tetrahedra" --these are two commonly used algorithms for volume rendering.
For an additional bell, the placement of the metaballs should depend on some sort of interactically controllable hierarchy.
Try out a demo application.
One difficulty with hierarchical modeling using primitives is the difficulty of building "organic" shapes.
It's difficult, for instance, to make a convincing looking human arm because you can't really show the bending of the skin and bulging of the muscle using cylinders and spheres.
There has, however, been success in building organic shapes using metaballs.
Implement your hierarchical model and "skin" it with metaballs. Hint: look up "marching cubes" and "marching tetrahedra" --these are two commonly used algorithms for volume rendering.
For an additional bell, the placement of the metaballs should depend on some sort of interactically controllable hierarchy.
Try out a demo application.
Metaball Demos:These demos show the use of metaballs within the modeler framework. The first demo allows you to play around with three metaballs just to see how they interact with one another.
The second demo shows an application of metaballs to create a twisting snake-like tube. Both these demos were created using the metaball implementation from a past CSE 457 student's project.
Demo 1: Basic Texture Mapped Metaballs
Demo 2: Cool Metaball Snake



 If you have a sufficiently complex model, you'll soon realize what a pain it is to have to play with all the sliders to pose your character correctly. Implement a method of adjusting the joint angles, etc., directly though the viewport.
For instance, clicking on the shoulder of a human model might select it and activate a sphere around the joint. Click-dragging the sphere then should rotate the shoulder joint intuitively.
For the elbow joint, however, a sphere would be quite unintuitive, as the elbow can only rotate about one axis. For ideas, you may want to play with the Maya 3D modeling/animation package, which is installed on the workstations in 228.
Credit depends on quality of implementation.
If you have a sufficiently complex model, you'll soon realize what a pain it is to have to play with all the sliders to pose your character correctly. Implement a method of adjusting the joint angles, etc., directly though the viewport.
For instance, clicking on the shoulder of a human model might select it and activate a sphere around the joint. Click-dragging the sphere then should rotate the shoulder joint intuitively.
For the elbow joint, however, a sphere would be quite unintuitive, as the elbow can only rotate about one axis. For ideas, you may want to play with the Maya 3D modeling/animation package, which is installed on the workstations in 228.
Credit depends on quality of implementation.



 Another method to build organic shapes is subdivision surfaces.
Implement these for use in your model. You may want to visit this to get some starter code.
Another method to build organic shapes is subdivision surfaces.
Implement these for use in your model. You may want to visit this to get some starter code.
Disclaimer: please consult the course staff before spending any serious time on these. These are all quite difficult, and credit can vary depending on the quality of your method and implementation.
Inverse kinematics









The hierarchical model that you created is controlled by forward kinematics; that is, the positions of the parts vary as a function of joint angles.
More mathematically stated, the positions of the joints are computed as a function of the degrees of freedom (these DOFs are most often rotations). The problem of inverse kinematics is to determine the DOFs of a model to satisfy a set of positional constraints, subject to the DOF constraints of the model (a knee on a human model, for instance, should not bend backwards).
This is a significantly harder problem than forward kinematics. Aside from the complicated math involved, many inverse kinematics problems do not have unique solutions. Imagine a human model, with the feet constrained to the ground. Now we wish to place the hand, say, about five feet off the ground. We need to figure out the value of every joint angle in the body to achieve the desired pose. Clearly, there are an infinite number of solutions. Which one is "best"?
Now imagine that we wish to place the hand 15 feet off the ground. It's fairly unlikely that a realistic human model can do this with its feet still planted on the ground. But inverse kinematics must provide a good solution anyway. How is a good solution defined?
Your solver should be fully general and not rely on your specific model (although you can assume that the degrees of freedom are all rotational).
Additionally, you should modify your user interface to allow interactive control of your model though the inverse kinematics solver.
The solver should run quickly enough to respond to mouse movement.
If you're interested in implementing this, you will probably want to consult the CSE558 lecture notes.
View-dependent adaptive polygon meshes









The primitives that you are using in your model are all built from simple two dimensional polygons. That's how most everything is handled in the OpenGL graphics world. Everything ends up getting reduced to triangles.
Building a highly detailed polygonal model often requires millions of triangles. This can be a huge burden on the graphics hardware. One approach to alleviating this problem is to draw the model using varying levels of detail. In the modeler application, this can be done by specifying the quality
(poor, low, medium, high). This unfortunately is a fairly hacky solution to a more general problem.
First, implement a method for controlling the level of detail of an arbitrary polygonal model. You will probably want to devise some way of representing the model in a file. Ideally, you should not need to load the entire file into memory if you're drawing a low-detail representation.
Now the question arises: how much detail do we need to make a visually nice image? This depends on a lot of factors. Farther objects can be drawn with fewer polygons, since they're smaller on screen. See Hugues Hoppe's work on View-dependent refinement of progressive meshes for some cool demos of this. Implement this or a similar method, making sure that your user interface supplies enough information to demonstrate the benefits of using your method. There are many other criteria to consider that you may want to use, such as lighting and shading (dark objects require less detail than light ones; objects with matte finishes require less detail than shiny objects).
Hierarchical models from polygon meshes









Many 3D models come in the form of static polygon meshes. That is, all the geometry is there, but there is no inherent hierarchy. These models may come from various sources, for instance 3D scans. Implement a system to easily give the model some sort of hierarchical structure. This may be through the user interface, or perhaps by fitting an model with a known hierarchical structure to the polygon mesh (see this for one way you might do this). If you choose to have a manual user interface, it should be very intuitive.
Through your implementation, you should be able to specify how the deformations at the joints should be done. On a model of a human, for instance, a bending elbow should result in the appropriate deformation of the mesh around the elbow (and, if you're really ambitious, some bulging in the biceps).







 Spot Light Shader - Create a shader that supports a spot light source, and add a third light source to your Modeler. We should be able to adjust the spot light parameters via sliders.
Spot Light Shader - Create a shader that supports a spot light source, and add a third light source to your Modeler. We should be able to adjust the spot light parameters via sliders. Blinn-Phong and Texture Mapping Shader - Extend your Blinn-Phong shader to support texture mapping. Remember to keep a copy of your original Blinn-Phong shader for grading.
Blinn-Phong and Texture Mapping Shader - Extend your Blinn-Phong shader to support texture mapping. Remember to keep a copy of your original Blinn-Phong shader for grading. Tessellated Procedural Shader - Make a shader that produces an interesting, repeating pattern, such as a brick pattern, without using a texture.
Tessellated Procedural Shader - Make a shader that produces an interesting, repeating pattern, such as a brick pattern, without using a texture.
