Please submit both code and writeup online by 6:30pm PST on Sunday, May 7, 2017. Please provide all code (sufficiently commented) so that we can run it ourselves. Submit your writeup as a PDF and limit to four pages with reasonable fonts and margins.
1.0 Read the paper Empirical Analysis of Predictive Algorithms for Collaborative Filtering. You need to read up to Section 2.1, and are encouraged to read further if you have time.
1.1 The dataset we will be using is a subset of the movie ratings data from the Netflix Prize. You can download it here. It contains a training set, a test set, a movies file, a dataset description file, and a README file. The training and test sets are both subsets of the Netflix training data. You will use the ratings provided in the training set to predict those in the test set. You will compare your predictions with the actual ratings provided in the test set. The evaluation metrics you need to measure are the Mean Absolute Error and the Root Mean Squared Error. The dataset description file further describes the dataset, and will help you get started. The README file is from the original set of Netflix files, and has been included to comply with the terms of use for this data.
1.2 Implement the collaborative filtering algorithm described in Section 2.1 of the paper (Equations 1 and 2; ignore Section 2.1.2) for making the predictions.
Extra-credit Add yourself as a new user to the training set. To do this, you will need to create a new user ID for yourself. Select some movies that you have seen among those in the training set, and add your ratings for them to the training set. Extend your system to output predictions for the movies you haven't rated, ranked in order of decreasing ratings. Do you agree with the predictions of your system? Check out some of the top ranked movies that you haven't seen (but only after you have finished work on the project).
Problem writeup:
2.1 You are a car mechanic and want to provide quick assesment of customers' car issues. Their car can either have a problem with the tires (low pressure, worn out, etc.) or problems with the suspension. For this problem we assume there is exactly ONE problem with the car. The customers normally report two symptoms: Is the car skidding or not and is car unstable at turns or not. From your experience you know that if the car has tire problems it is likely to skid with 50% chance while if it has suspension problems it will skid 20% of the time. You also know that a car is unstable with 30% chance if the tires are bad but with 70% if the suspension is bad. From prior experience you know that 70% of time cars have issues with their suspension and 30% with their tires.
a. You do a quick test drive and discover the car is unstable at turns but is not skidding. How likely is it to be tire or suspension problem? (Hint: To solve this problem, start by drawing a Bayes' net with variables C(Car issue), S(skidding) and T(stable or not at turns) and write down the conditional probability tables.)
From experience you know that whenever a customer reports the problems with their car they are only 75% correct, and 25% of the time all the reported symptoms are the exact opposite of the way the car actually behaves.
b. What are the probabilities of the car condition given that the customer now claims that his car is skidding but otherwise stable?
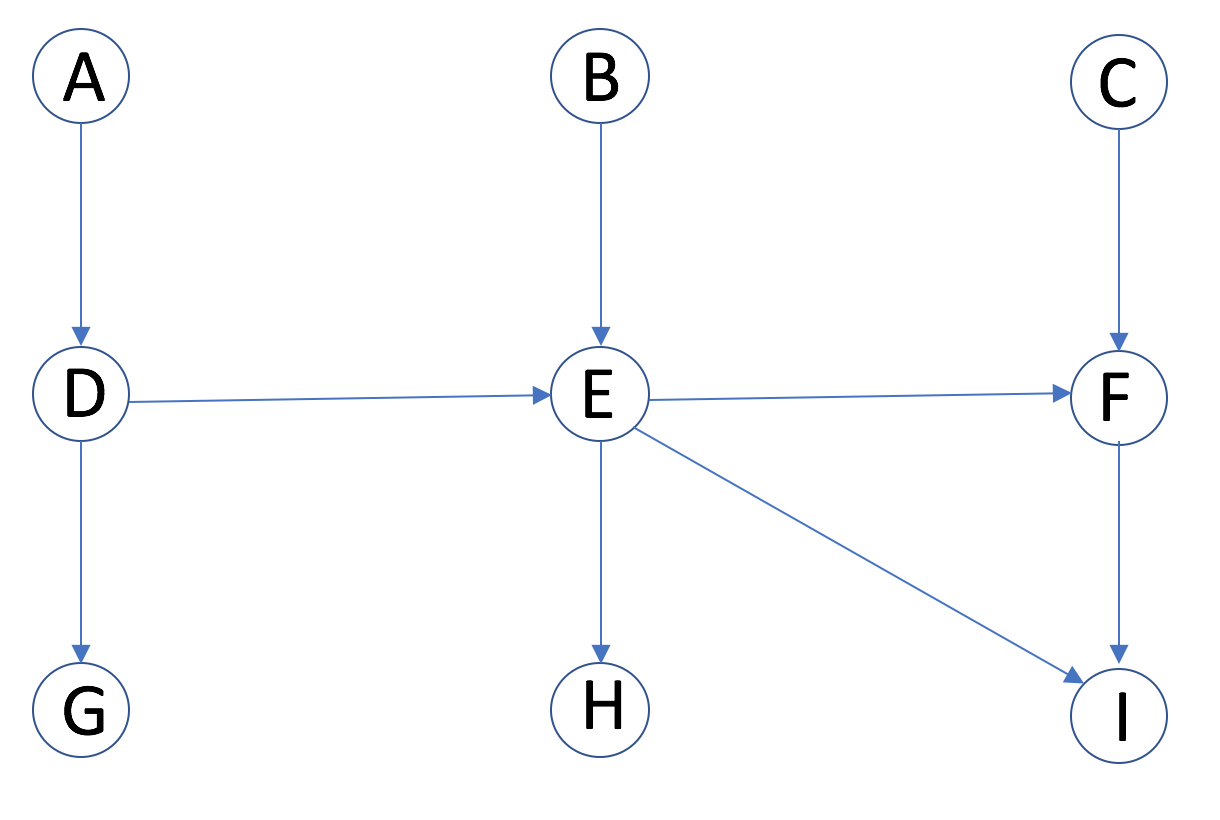
2.2 Consider the following Bayesian network:

Which of the followings are guaranteed to be true without making any additional conditional independence assumptions, other than those implied by the graph? (Mark all true statements)
2.3 Consider the following Bayesian network:
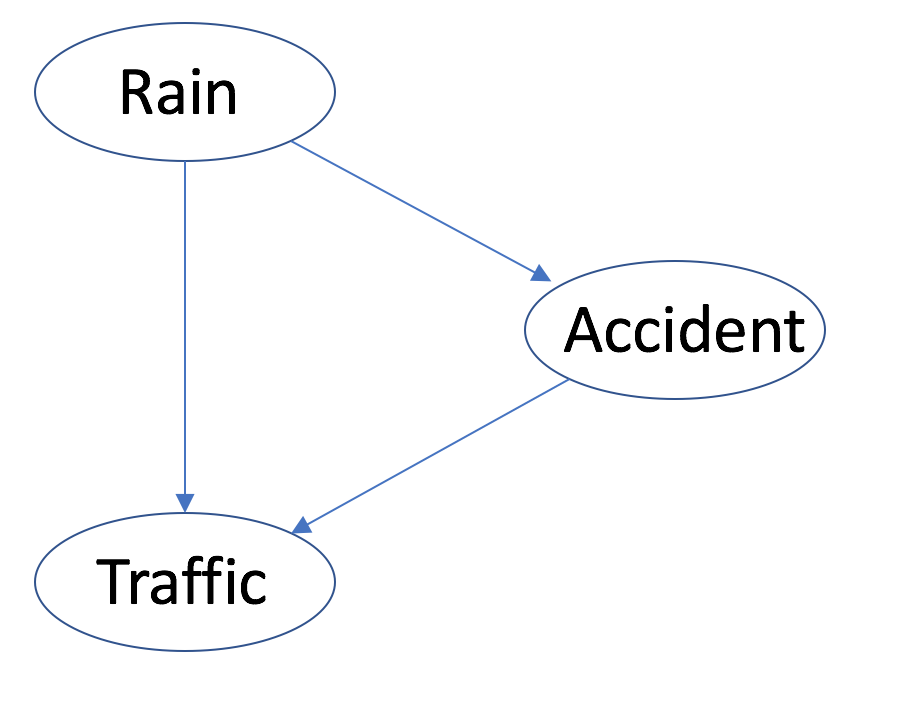
Any of the “Rain (R)”, “Accident (A)”, “Traffic (T)” are Boolean nodes. Suppose you have a training set composed of the following examples in the form (R,A,T), with "?" indicating a missing value: (1,1,0), (1,1,1), (1,1,1), (0,1,1), (0,1,?), (0,0,0), (0,0,?). Show the first iteration of EM algorithm (initial parameters, E-step, M-step), assuming the parameters are initialized ignoring missing values.