`|= `@=

Applied Algorithms Anna Karlin, 426C Sieg
CSE 589, Autumn 2000

Homework # 8
Due December 6

1.

Suppose that we had future knowledge of the full sequence of operations (Lookup, Insert or Delete) to be performed on a particular Splay tree. Consider the modification to the Splay tree algorithm that does everything exactly the same except that, on the operation Lookup(K), no splay on K is performed unless there is a subsequent Lookup, Insert or Delete of key K. Does the modified algorithm still have amortized $O(\log n)$ cost per operation, starting from an empty tree? If so, give a brief argument. If not, give a counterexample.

2.

Suppose in our Splay tree analysis, rather than starting with an empty tree, we are presented with an initial (arbitrary) binary search tree T containing n nodes.

(a)

Give the best upper bound you can (using big Oh notation) on the amount of money we will need to initially invest in the tree T in order to make sure the Money Invariant holds. (The Money Invariant says that each node has a number of dollars equal to its rank).

(b)

Use your answer to part (a) to give the best bound you can (using Big Oh notation) on the total cost of performing m Lookup operations using the Splay tree algorithm, starting with the tree T (as opposed to starting with an empty tree).

3.

(Extra credit) Public-Key Cryptography:

(a)

What is the primary advantage of public-key cryptography over symmetric cryptography?

(b)

Consider a message M encrypted using the RSA public-key cryptosystem. Let E(M) be the ciphertext produced. Give an algorithm for determining M. What is the running time of your algorithm as a function of the number of bits in n (the modulus =pq)?

(c)

To encrypt a plaintext M using the RSA public-key cryptosystem, the message is first broken up into chunks of at most k bits, where k is the number of bits in the modulus n. Why can't we just encrypt the entire message in one fell swoop?

4.

(Extra credit) Consider the following symmetric cryptosystem, the exponentiation cipher. First, choose a prime modulus m, known to everyone. Choose a key k less than m at random. (We will see later that not all keys k are possible.) k is kept secret. Then the encryption function E_k(M) is defined as

$$E_k(M) = M^k ({\mbox{ mod }}m).$$

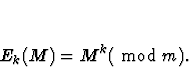
Let s be the mod $\phi (m)$ multiplicative inverse of k. Then the decryption function is

$$D_k(C) = C ^s ({\mbox{ mod }}m),$$

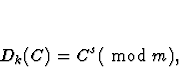
where C= E_k(M).

(a)

Prove that the cryptosystem works, i.e., that D_k(C) = M.

(b)

Characterize the set of keys k <m for which this system works.

(c)

Give an argument for why this cryptosystem is probably not vulnerable to known plaintext attack (i.e., recovering the key, given a message and its encryption).