


Next: About this document ...
`|=
`@=
Applied Algorithms Anna Karlin, 426C Sieg
CSE 589, Autumn 2000
Homework # 5
Due 4pm, November 3
Reading: see slides
Problems
- 1.
- Consider the following LP.
maximize 3x + 5y
subject to 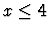 ,
,
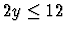 ,
,
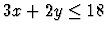 ,
,
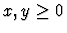 .
.
- Draw the feasible set.
- Determine graphically the solution.
- Which vertices of the feasible set would the
simplex algorithm visit en route to the solution?
- 2.
- What is the dual problem of the following
linear program?
maximize 4x+7y+2z
subject to 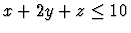 ,
,
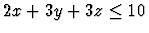 ,
,
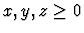 .
.
- 3.
- Prove that the subgraph isomorphism problem is NP-complete.
In this problem, you are given two graphs G=(V1,E1) and H=(V2,E2),
and you
are asked if G contains a subgraph isomorphic to H, i.e., does there
exist a subset
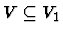 and a subset
and a subset
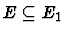 ,
such that (a) V and V2 have the same
size, (b) E and E2 have the same size, and (c)
there exists a one to one function
,
such that (a) V and V2 have the same
size, (b) E and E2 have the same size, and (c)
there exists a one to one function
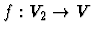 satisfying
satisfying 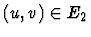 if and only if
if and only if
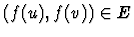 ?
?
- 4.
- You are a traveling salesperson of the new millenium. Your boss
has asked you to visit n cities, each exactly once,
and you are planning your
flight itinerary. You do not care about the cost of
travel - the company is going to pay your expenses anyway.
What you want to maximize is the benefits you will receive
as a frequent flyer! In other words, you want to maximize
the length of the entire trip.
Do not worry about choosing different airlines. You just want
to maximize the total mileage. Prove that this problem
is NP-complete, and suggest heuristic approaches to it.
- 5.
- Find, by either searching the web, searching
the literature, or talking to people a real-life important
problem that is NP-complete. It should not be one of
the problems that's been mentioned in class.
How is the problem solved in practice? (Either find out,
or come up with your own idea.)
- 6.
- Extra Credit Consider the following closest-point heuristic
for building an approximate traveling-salesman tour.
Begin with a trivial cycle consisting of a single arbitrarily
chosen vertex. At each step, identify the vertex u
that is not on the cycle but whose distance to any vertex
on the cycle is minimum. Suppose that the vertex on the cycle
that is nearest u is vertex v. Extend the cycle to include
u by inserting u just after v. Repeat until all vertices
are on the cycle. Prove that this heuristic returns a tour
whose total cost is not more than twice the cost of an optimal tour.



Next: About this document ...
Ashish Sabharwal
2000-10-25