`|= `@=

Applied Algorithms Anna Karlin, 426C Sieg
CSE 589, Autumn 2000

Homework # 3
Due 4pm, October 20

Reading: Skiena, Section 8.4.9; CLR, chapter 27

Problems

1.

Suppose we are given the minimum spanning tree T of a given graph with n vertices and m edges, and a new edge e=(u,v) of weight w that we will add to G. Give an efficient algorithm to find the minimum spanning tree of the graph G+e. Your algorithm should run in O(n) time.

2.

Dijkstra's algorithm for finding shortest paths assumes that all edges have positive cost. A proposal for solving the case where edges have negative weights is to add the same amount of weight to each edge in the graph, so that all edge weights become positive, and then run Dijsktra's algorithm on the modified graph. Prove that this method does not work.

3.

Will NOT be graded. Consider the problem of finding a maximum flow in a network with both lower bounds and upper bounds (capacities) on each edge. Assume that all bounds are integer. Suppose you are presented with a feasible flow (a flow that satisfies all the lower and upper bounds and has conservation of flow). Give an algorithm for converting the feasible flow to a maximum flow. What can you say about the running time of your algorithm?

4.

We discussed algorithms for the following graph problems.

• Finding a minimum spanning tree for a weighted graph.
• Finding shortest paths in a weighted graph with non-negative weights.
• Finding either a negative-weight cycle or shortest paths in a weighted graph with arbitrary edge weights.
• Finding a maximum flow in a network.
• Finding a minimum cost max flow in a network.

For each of the following problems, describe how it could be modeled as a graph problem and solved with the aid of one or more of the above known algorithms, or ideas involved therein.

(a)

Will NOT be graded. Arbitrage is the use of discrepancies in currency exchange rates to transform one unit of currency into more than one unit of the same currency. For example, suppose that 1 U.S. dollar buys 0.7 British pounds, 1 British pound buys 9.5 French francs, and 1 French franc buys 0.16 U.S. dollars. Then, by converting currencies, a trader can start with 1 U.S. dollar and buy 0.7 x 9.5 x 0.16 = 1.064 U.S. dollars, thus turning a profit of 6.4 percent.

Suppose we are given n currencies 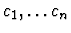$c_1,\ldots c_n$ and an n x n table R of exchange rates, such that one unit of currency c_i buys R[i,j] units of currency c_j.

How would you go about figuring out whether or not there exists a sequence of currencies 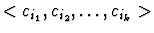$<c_{i_1}, c_{i_2},\ldots, c_{i_k}>$ such that

$$R[i_1,i_2]\cdot R[i_2,i_3]\cdots R[i_{k-1},i_k]\cdot R[i_k,i_1] >1.$$

(b)

Will NOT be graded A problem for temporary services industries is the efficient distribution and utilization of skilled personnel. Each month many individuals vacate positions and many people become available for assignment. Each job has particular characteristics and skill requirements, while each person from the pool of available personnel has specific skills and preferences. Suppose that we use this information to compute the utility (or desirability) d_ij of each possible assignment of a person to a job. How would you go about assigning personnel to the vacancies in a way that maximizes the total utility of all the assignments?

(c)

In certain situations, it is desirable to store data specified in the form of a two-dimensional array more efficiently than storing all the elements of the array. Assume that the rows of the array have many similar entries and differ in only a few places. Since the entities in the rows are similar, one approach for saving memory is to store one row, called the reference row, completely and to store only the differences between some of the rows so that we can derive each row from these differences and the reference row. Let c_ij denote the number of different entries in rows i and j; that is, if we are given row i, then by making c_ij changes to the entries in this row we can obtain row j and vice versa. For example, suppose that the array contains four rows, represented by R₁,R₂,R₃,R₄, and we decide to treat R₁ as a reference row. Then one plausible solution is to store the differences between R₁ and R₂, R₂ and R₄, and R₁ and R₃. Clearly from this solution, we can obtain rows R₂ and R₃ by making c₁₂ and c₁₃ changes to the elements in row R₁. Having obtained row R₂, we can make c₂₄ changes to the elements of this row to obtain R₄. The storage requirement of this scheme is (the data in R₁) +c₁₂+c₁₃+c₂₄. How would you go about computing which row differences to store in order to minimize the total storage requirement? Assume that the reference row is always the row with the least amount of data.

(d)

A certain well-known document processing program uses an optimization procedure to decompose a paragraph into several lines so that when lines are left- and right- adjusted, the appearance of the paragraph will be most attractive. Suppose that a paragraph consists of n words and that each word is assigned a sequence number. Suppose that a formula is available to compute c_ij, the ugliness of a line if it begins with word i and ends with the word j-1. Given the c_ij's, how would you solve the problem of decomposing the paragraph into several lines of text in order to minimize the total ugliness of all the lines in the paragraph.