EE/CSE 576, Spring '17 Homework 1: Filtering, Edge finding and Clustering
DUE: April 15, 2017 (Saturday) 11:59 P.M.
Late date: April 17, 2017 (Monday) 11:59 P.M. (Late policy: 10% penalty per day)
Total points: 35 (+10 extra credit)
Before you start:
Download the zip file here.
Please read the word document on Getting started with Qt.docx to install and use Qt. Pay careful attention to all the instructions.
Assignment Description:
For this assignment, you'll be implementing the functionality of the ImgFilter program, which allows you to load an image and apply various images filters and K-means clustering. You need to write code for some basic functions, many of which will be needed in the future assignments too.
In the project, you should only update the file - "Project1.cpp". The other files like "mainwindow.cpp" and "main.cpp" contain code to execute the application. When you compile and run the "ImgFilter" project, a user interface (UI) will appear on the screen. The buttons in the UI will call the corresponding functions in "Project1.cpp". Several of the buttons have already been implemented, including "B/W", "Add noise", "Mean" and "Half size". The implementations of these buttons are in "Project1.cpp", and should provide helper sample code. Please see these functions to understand how to work with images in Qt.
The QImage class in the Qt package provides a hardware-independent image representation and the QRgb class holds a color pixel. You can find more information here. The origin of the image is the top left corner and the width and height of the image is accessible through the global variables imageWidth and imageHeight respectively. For this assignment, the input image is converted from QImage form to a matrix form (having double values). The size of the image matrix is (imageWidth * imageHeight) * 3 (for 3 color channels). Thus, a pixel of 'image' at position (c,r) in color channel say 0 (red) is mapped to the matrix 'Image' as: Image[r * imageWidth + c][0] = qRed(image.pixel(c,r)). Refer to the function ConvertQImage2Double() provided in the starter code.
Important note: In all the functions, if you perform any operation on the input image by calling a function, the original image is changed. If you want to retain the original image for a task, first create a copy of the original image and perform the operations on the copy. Also, all the operations are performed on each of the 3 color bands (R, G and B as 0, 1 and 2) separately unless mentioned otherwise.
What to turn in:
To receive credit for the project, you need to turn in HERE a single .zip file (name it as yourfullname.zip) containing the completed file "Project1.cpp" and the requested images for each task. Please write necessary comments in your code so that it is easily understandable.
Please Note: We have modified the original assignment to convert the input image from QImage class to double class. Please do not use old version of this code. Leave the resultant images in double form; they are converted back to QImage class in the mainwindow.cpp file which you don't need to worry about.
TASKS:
Task 1: Convolution (4 points)
Implement the function
Convolution(double **image, double *kernel, int
kernelWidth, int
kernelHeight, bool
add) to convolve an image with a kernel of size kernelHeight*kernelWidth. Use zero-padding around the borders for simplicity (see first extra credit task if you wish to do otherwise).
Here:
Write a general convolution function that can handle all possible cases as mentioned above. You can get help from the convolution part of the function MeanBlurImage to write this function. Note that MeanBlurImage deals with image in QImage form, but you need to write in double form.
Read the other parts of Project1.cpp provided in the starter code for further help.
Task 2: Gaussian Blur (3 points)
Implement the function GaussianBlurImage(double **image, double sigma) to Gaussian blur an image. "sigma" is the standard deviation of the Gaussian. Use the function MeanBlurImage as a template, create a 2D Gaussian filter as the kernel and call the Convolution function of Task 1 (details). Normalize the created kernel using the given NormalizeKernel() function before convolution. For the Gaussian kernel, use kernel size = 2*radius + 1 (same as the Mean filter) and radius = (int)(ceil(3 * sigma)) and the proper normalizing constant.
To do: Gaussian blur the image "Seattle.jpg" using this function with a sigma of 4.0, and save as "task2.png".
Task 3: Separable Gaussian Blur (3 points)
Implement the function SeparableGaussianBlurImage (double **image, double sigma) to Gaussian blur an image using separate filters. "sigma" is the standard deviation of the Gaussian. The separable filter should first Gaussian blur the image horizontally, followed by blurring the image vertically. Call the convolution function twice, first with the horizontal kernel and then with the vertical kernel. Use the proper normalizing constant while creating the kernel(s) and then normalize using the given NormalizeKernel() function before convolution. The final image should be identical to that of GaussianBlurImage.
To do: Gaussian blur the image "Seattle.jpg" using this function with a sigma of 4.0, and save as "task3.png".
Task 4: Image derivatives (4 points)
Implement the functions FirstDerivImage_x(double **image, double sigma), FirstDerivImage_y(double **image, double sigma) and SecondDerivImage(double **image, double sigma) to find the first and second derivatives of an image and then Gaussian blur the derivative image by calling the GaussianBlurImage function.
"sigma" is the standard deviation of the Gaussian used for blurring.
To compute the first derivatives, first compute the x-derivative of the image (using the horizontal 1*3 kernel: {-1, 0, 1}) followed by Gaussian blurring the resultant image.
Then compute the y-derivative of the original image (using the vertical 3*1 kernel: {-1, 0, 1}) followed by Gaussian blurring the resultant image.
The second derivative should be computed by convolving the original image with the 2-D Laplacian of Gaussian (LoG) kernel: {{0, 1, 0}, {1, -4, 1}, {0, 1, 0}} and then applying Gaussian Blur.
Note that the kernel values sum to 0 in these cases, so you don't need to normalize the kernels.
Remember to add 128 to the final pixel values in all 3 cases, so you can see the negative values. Note that the resultant images of the two first derivatives will be shifted a bit because of the uneven size of the kernels.
To do: Compute the x-derivative, the y-derivative and the second derivative of the image "LadyBug.jpg" with a sigma of
1.0 and save the final images as "task4a.png", "task4b.png" and "task4c.png" respectively.
Task 5: Image Sharpening (3 points)
Implement the function SharpenImage(double **image, double sigma, double alpha) to sharpen an image by subtracting the Gaussian-smoothed second derivative of an image, multiplied by the constant "alpha", from the original image. "sigma" is the Gaussian standard deviation. Use SecondDerivImage and subtract back off the 128 that second derivative added on. Note that this is slightly different from the lecture slide, but equivalent.
To do: Sharpen "Yosemite.png" with a sigma of 1.0 and alpha of
5.0 and save as "task5.png".
Task 6: Edge Detection (3 points)
Implement SobelImage (double **image) to compute edge magnitude and orientation information. The input image is converted into grayscale in the starter code. The input image still has 3 channels but all the channels have the same values (grayscale values), so you can use any of the channels for further operations. Use the standard Sobel masks in X and Y directions: {{-1, 0, 1}, {-2, 0, 2}, {-1, 0, 1}} and {{1, 2, 1}, {0, 0, 0}, {-1, -2, -1}} respectively to compute the edges. Note that the kernel values sum to 0 in these cases, so you don't need to normalize the kernels before convolving. Divide the image gradient values by 8 before computing the magnitude and orientation in order to avoid spurious edges. SobelImage should then display both the magnitude and orientation of the edges in the image (see commented code in Project1.cpp for displaying orientations and magnitudes).
To do: Compute Sobel
edge magnitude and orientation on "LadyBug.jpg" and save as "task6.png".
Task 7: Bilinear Interpolation (3 points)
Implement the function BilinearInterpolation(double **image, double x, double y, double rgb[3]) to compute the linearly interpolated pixel value at the point (x,y) using bilinear interpolation.
Both x and y are real values (see here). Put the red, green, and blue interpolated results in the vector "rgb".
To do: The function RotateImage is already implemented in Project1.cpp and uses BilinearInterpolation to rotate an image. Rotate the image "Yosemite.png" by 20 degrees and save as "task7.png".
Task 8: Finding edge peaks (4 points)
Implement the function FindPeaksImage(double **image, double thres) to find the peaks of edge responses perpendicular to the edges.
The edge magnitude and orientation at each pixel are to be computed using the Sobel operators. The original image is again converted into grayscale in the starter code. A peak response is found by comparing a pixel's edge magnitude to that of the two samples perpendicular to the edge at a distance of
one pixel, which requires the BilinearInterpolation function (Hint: You need to create an image of magnitude values at each pixel to send as input to the interpolation function). If the pixel's edge magnitude is e and those of the other two are e1 and e2, e must be larger than "thres" (threshold) and also larger than or equal to e1 and e2
for the pixel to be a peak response. Assign the peak responses a value of 255 and everything else 0. Compute e1 and e2 as follows:
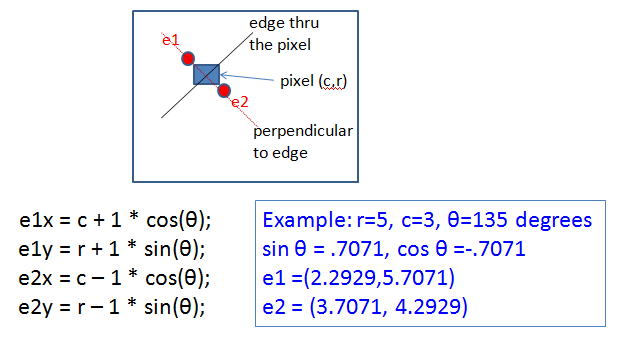
To do: Find the peak responses in "Circle.png" with thres = 40.0 and save as "task8.png". Note that you may get double edges at the bottom of the circles because they are slightly flat at the bottom in the original image.
Task 9 (a): K-means color clustering with random seeds (5 points)
Implement the function RandomSeedImage(double **image, int num_clusters)
to perform K-Means Clustering on a color image with randomly selected initial cluster centers in the RGB color space.
"num_clusters" is the number of clusters into which the pixel values in the image are to be clustered.
Use "(rand() % 256, rand() % 256, rand() % 256)" as RGB values to create #num_clusters centers, assign each pixel of the image to its closest cluster center and then
update the cluster centers with the average of the RGB values of the pixels belonging to that cluster until convergence.
Use max iteration # = 100 and L1 distance between pixels, i.e. dist = |Red1 - Red2| + |Green1 - Green2| + |Blue1 - Blue2|.
The algorithm converges when the sum of the L1 distances between the new cluster centers and the previous cluster centers is less than epsilon*num_clusters.
Choose epsilon = 30 (or anything suitable). Note: Your code should account for the case when a cluster contains 0 pixels during an iteration.
Also, since this algorithm is random, you will get different resultant images every time you call the function.
To do: Perform random seeds clustering on "Flower.png" with num_clusters = 4 and save as "task9a.png".
Task 9 (b): K-means color clustering with pixel seeds (3 points)
Implement the function PixelSeedImage(double **image, int num_clusters)
to perform K-Means Clustering on a color image with initial cluster centers sampled from the image itself in the RGB color space.
"num_clusters" is the number of clusters into which the pixel values in the image are to be clustered.
Choose a pixel and make its RGB values a seed if it is sufficiently different (dist(L1) >= 100) from already-selected seeds.
Repeat till you get #num_clusters different seeds.
Use max iteration # = 100 and L1 distance between pixels, i.e. dist = |Red1 - Red2| + |Green1 - Green2| + |Blue1 - Blue2|.
The algorithm converges when the sum of the L1 distances between the new cluster centers and the previous cluster centers is less than epsilon*num_clusters.
Choose epsilon = 30.
To do: Perform pixel seeds clustering on "Flags.png" with num_clusters = 5 and save as "task9b.png".
Bell and Whistles (EXTRA CREDIT: Whistle = 1 point, Bell = 2 points)
![]()
Implement an improved image border padding method, i.e. "fixed" or "reflected", inside the Convolution function.
Refer to Lecture 2 notes for details. Comment this portion of the code if you plan to use zero-padding for the tasks. Also write a comment in the Convolution function if you have implemented this task.
![]()
Histogram K-means implementation - Implement the function HistogramSeedImage(double **image, int num_clusters) for selecting the K-Means cluster seeds intelligently from the image using its color histogram.
The seed selection should be automatic, given the histogram (write code to compute histogram) and the number of seeds to be selected.
One way to go is to find the peaks in the color histogram as candidates for seeds. Take "Flower.png" as the input image and save the resultant image as "histogramtask.png". Credit will still be given if you convert the image into grayscale and operate on it. You are free to choose any value of epsilon and num_clusters to get a good result.
![]()
Implement the function MedianImage(double **image, int radius) to apply the median filter on a noisy image.
Choose the kernel size as 2*radius + 1. Convert the input image into grayscale first, then add noise of magnitude 20.0 (without colorNoise) using the AddNoise function, and then apply the median filter. You will see that the noise of the noisy image has been reduced by the median filter.
Take "Seattle.jpg" as the input image and save the final image as "mediantask.png".
![]()
Implement the function BilateralImage(double **image, double sigmaS, double sigmaI) to bilaterally blur an image. "sigmaS" is the spatial standard deviation in the spatial domain and "sigmaI" is the standard deviation in intensity/range. Hint: The code should be very similar to GaussianBlurImage. Here's the info about bilateral filtering. Take the "Yosemite.png" image as input and save the resultant image as "bilateraltask.png".
![]()
Implement the function HoughImage(double **image) to compute the Hough transform using the peaks found from FindPeaksImage. Take any suitable image among the given images as the input. You may just output a bunch of images, i.e. , 1.jpg, 2.jpg, 3.jpg, etc. or make a gif animation.
![]()
![]()
Develop a smarter K-Means variant that determines the best value for K by evaluating statistics of the clusters. Implement the function SmartKMeans(double **image) using "Flags.png" and save the result as "kmeanstask.png". Some possible methods to try:
1. Start from the color histogram, as K is closely related to the number of peaks in the histogram. Not all the peaks are necessary as you want only the dominant ones, so you should pick the ones that occupy a certain fraction of the image in terms of pixels.
2. Try clustering using different Ks, and pick the best one. The metric could be related to the distance between clusters and the variance within each cluster.
3. You are free to come up with your own ways.