CSE 576 Computer Vision

Project 1: Feature Detection and Matching

Name: Kuan-Hui Lee

Introduction

In this project, I implement Harris corner detection and Multi-Scale Oriented Patches (MOPS) descriptor [1] to detect discriminating features in an image and find the best matching features in other images. I use MOPS descriptor because it is not only scale invariant but also orientation invariant. The reason why MOPS is scale invariant is that MOPS utilizes Gaussian of pyramid to describe the feature, and the reason why MOPS is orientation invariant is that MOPS consider the orientation of the interest points by rotating to the dominant orientation. In the experiments, I evaluate the performance of MOPS descriptor and simple square window descriptor on a suite of benchmark images, and compare them with the state-of-art feature descriptor (SIFT) [2]. 

Multi-Scale Oriented Patches (MOPS) Feature Descriptor

Multi-Scale Oriented Patches (MOPS) are a minimalist design for local invariant features. They consist of a simple bias-gain normalized patch, sampled at a coarse scale relative to the interest point detection. The low frequency sampling helps to give insensitivity to noise in the interest point position. The interest points I use are multi-scale Harris corners. For each input image , a Gaussian image pyramid is formed, using a subsampling rate s = 2 and pyramid smoothing width σ_p = 1.0. Interest points are extracted from each level of the pyramid. First, the image is transferred to gray level, and then Gaussian pyramid is built with different octaves. The blurred images are used for the next (higher) octave to create the blurred images, and so forth. The idea is shown in the Figure 1.

Figure 1

The Harris matrix at level l and position (x, y) is the smoothed outer product of the gradients

We set the integration scale and the derivative scale . To find interest points, we first compute the “corner strength” function:

which is the harmonic mean of the eigenvalues of H. Interest points are located where the corner strength is a local maximum in a 3 × 3 neighborhood, and above a threshold t = 10.0. Once local-maxima have been detected, their position is refined to sub-pixel accuracy by fitting a 2D quadratic to the corner strength function in the local 3×3 neighborhood and finding its maximum. For each interest point, we also compute an orientation θ, where the orientation vector [cosθ, sinθ] = u/|u| comes from the smoothed local gradient

The integration scale for orientation is . A large derivative scale is desirable so that the gradient field varies smoothly across the image, making orientation estimation robust to errors in interest point location.

After detecting the interest points, I need to extract a description of the local image structure that will support reliable and efficient matching of features across images. Given an oriented interest point (x, y, l, θ), I sample a 9 × 9 patch of pixels around the sub-pixel location of the interest point, using a spacing of s = 5 pixels between samples (Figure 2). To avoid aliasing, the sampling is performed at a higher pyramid level, such that the sampling rate is approximately once per pixel (the Nyquist frequency). After sampling, the descriptor vector is normalized so that the mean is 0 and the standard deviation is 1. This makes the features invariant to affine changes in intensity (bias and gain). Finally, we extract the 9 × 9 descriptor patch d_i to form a 81 dimensional descriptor vector, from the Gaussian pyramid.

Figure 2

Experimental Results

There are 3 experiments in the project. First experiment tests two testing datasets, graf and Yosemeti, second experiments tests benchmark testing datasets: bikes, graf, leuven, and wall, and the third experiment tests other datasets: beaver, predator, and house. The feature type of Harris corner for executable is 2, and the MOPS is 3.

ROC datasets

In the first experiment, I use Harris corner detection to detect the interested points, and then use simple square window as the descriptor. Then, I use Multi-Scale Oriented Patches (MOPS) as the descriptor. Besides, I also use Scale-invariant feature transform (SIFT) descriptor as the comparison. Each descriptor is applied two kinds of matching scheme: SSD matching and ratio test matching. The ROC curves with different settings are shown as Figure 3, and the AUC values are shown in the Table I. As we can see in the Figure 3 and Table I, the results of the MOPS are better than the simple square window, especially by using ratio test matching. In the Yosemeti testing set, the AUC results of the MOPS are much better than square window descriptor. This is because Yosemeti testing set only has a translation between the images. The matched images are shown beside the ROC curves; here I just show the results with MOPS feature matched by ratio matching.

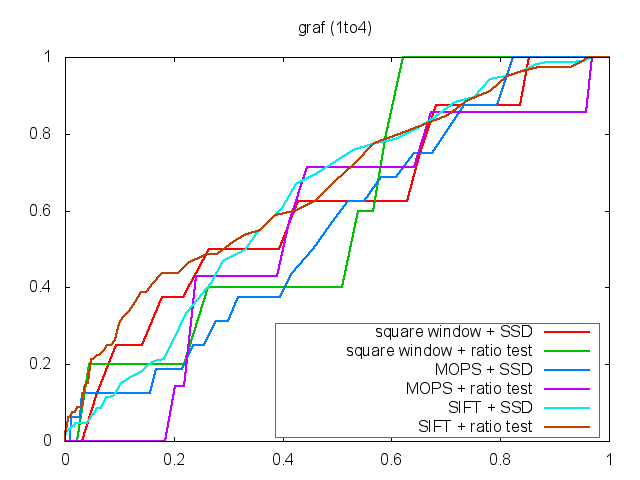
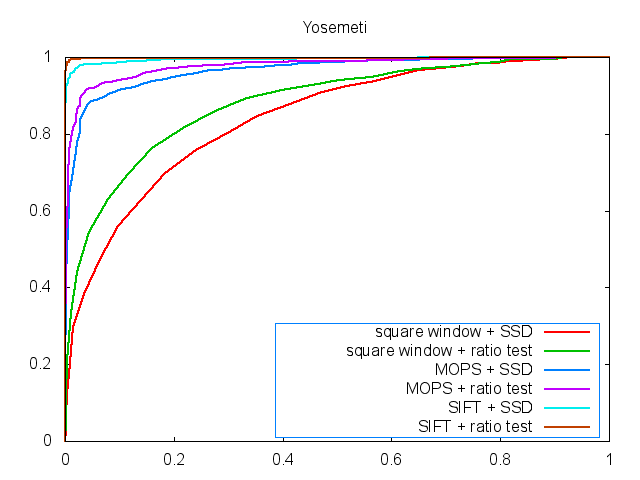
Figure 3

	graf (1to2)	graf (1to4)	Yosemeti (1to2)
square window+SSD	0.616209	0.603844	0.841205
square window+ratio	0.572349	0.614171	0.881062
MOPS+SSD	0.635616	0.560175	0.965544
MOPS+ratio	0.636376	0.556795	0.976857
SIFT+SSD	0.932023	0.631943	0.994692
SIFT+ratio	0.964775	0.662414	0.998442

Table I

Benchmark datasets

In the second experiment, I test datasets in the benchmark. There are 4 datasets in the testing benchmark: bikes, graf, leuven, and wall. Here I compare two descriptors: simple square window and MOPS, with both SSD and ratio test matching scheme. Table II shows the average error and AUC value of the datasets in SSD matching scheme, while Table III shows the average error and AUC value of the datasets in ratio matching scheme. As shown in the tables, MOPS descriptor has better results than the square window ones, and ratio matching performs better than SSD matching.

SSD matching		bikes	graf	leuven	wall
Square window	Avg error (pixel)	351.518998	298.458099	267.831739	315.500524
	AUC	0.274419	0.539099	0.510582	0.539968
MOPS	Avg error (pixel)	292.039042	294.667663	225.386793	317.429353
	AUC	0.836322	0.565938	0.821942	0.832833

Table II

Ratio matching		bikes	graf	leuven	wall
Square window	Avg error (pixel)	355.837239	268.734670	279.868046	324.845142
	AUC	0.318105	0.583318	0.581805	0.564149
MOPS	Avg error (pixel)	309.44252	280.091299	253.596348	340.733291
	AUC	0.893496	0.598450	0.883778	0.807800

Table III

bikes

leuven

wall

Figure 4

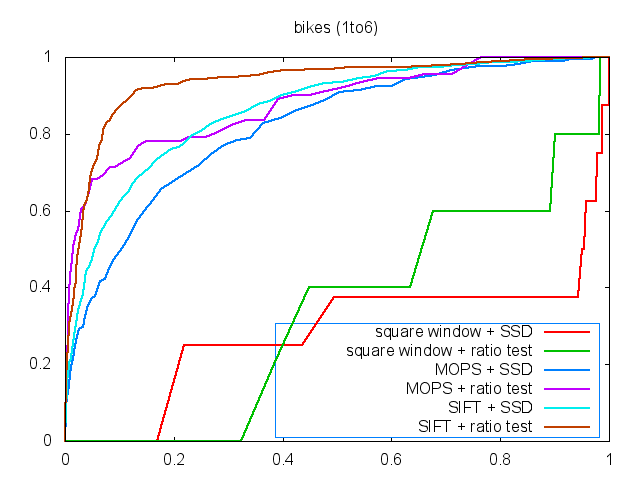
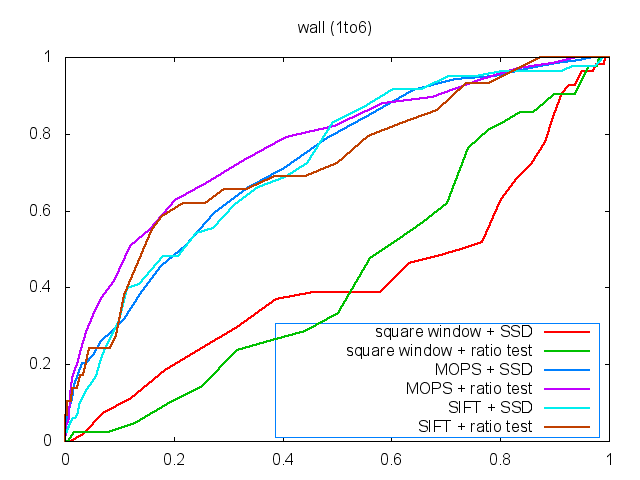
Figure 4 shows the MOPS matched results and ROC curves. As we can see, MOPS descriptor performs well than simple square window descriptor. In the case of bikes, the features still can be matched even if the images are blurred. This is because the characteristics of the Gaussian pyramid. In the case of leuven, MOPS descriptor still performs well when intensities become low. In the case of wall, MOPS’s performance is good enough when compared to the SIFT.

My datasets

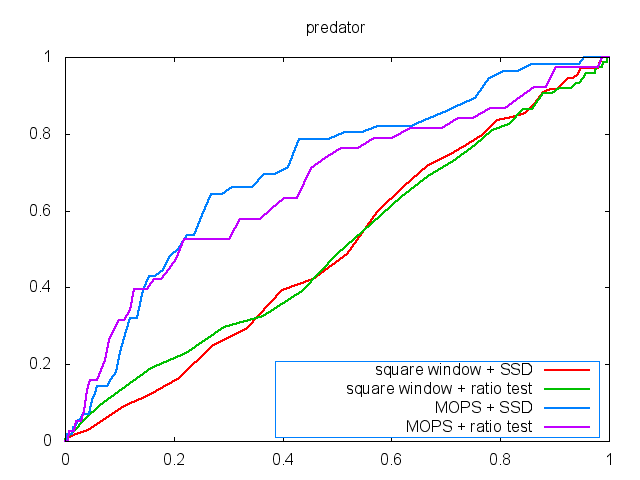
In the third experiment, I test 3 of other datasets: beaver, predator, and house. The beaver dataset test the ability of the scale issues, while the predator dataset tests the rotational issues. The homography matrix between the images in each pair is constructed by SIFT features. The images and the experimental results, including ROC curves and AUC values are shown in the Figure 5 and Table IV, separately. As shown in the figures, the MOPS descriptor performs better results and achiever higher AUC values in the testing datasets.

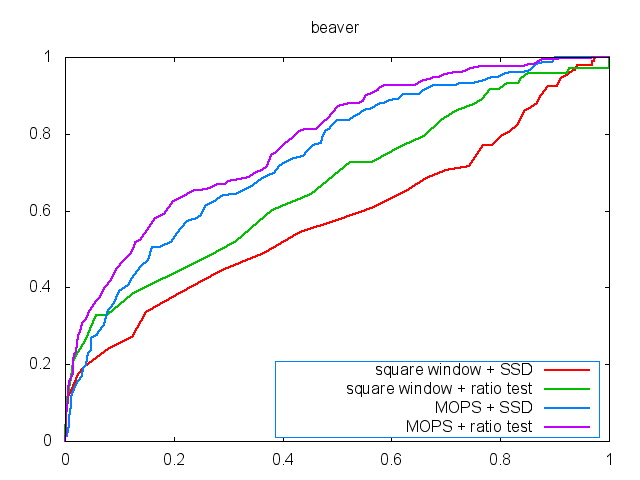
beaver

(cannot show the matched result due to image size is too large to catch)

predator

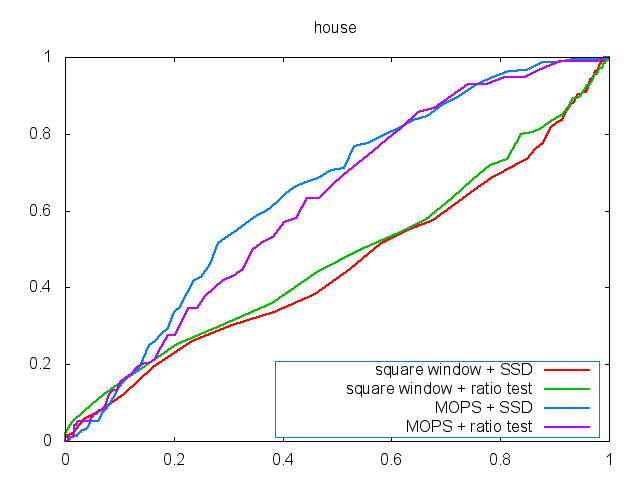
house

Figure 5

	beaver	predator	House
square window+SSD	0.581502	0.498501	0.455505
square window+ratio	0.741565	0.504360	0.479408
MOPS+SSD	0.668211	0.703020	0.647480
MOPS+ratio	0.782887	0.665649	0.621202

Table IV

Conclusion

In this project, I implement Harris corner detection and Multi-Scale Oriented Patches (MOPS) descriptor to detect discriminating features in an image and find the best matching features in other images. The performance is quite good when compared to the simple square window descriptor. Because of considering the Gaussian pyramid and orientation, it performs much better especially when scale and orientation issues happen. However, the performance cannot achieve that of SIFT descriptor, because SIFT descriptor also considers the orientation of the gradient.

Reference

[1] M. Brown, R. Szeliski and S. Winder, “Multi-image matching using multi-scale oriented patches,” International Conference on Computer Vision and Pattern Recognition, pp. 510-517.

[2] David G. Lowe, "Distinctive image features from scale-invariant keypoints," International Journal of Computer Vision, 60, 2, pp. 91-110, 2004.