Feature Detection and Matching

By: Caleb Woodruff

Computer Vision, CSE 576, Spring 2013, Project 1

Introduction

For this project we wish to recognize features across multiple images.  This is necessary for finding the relative positioning of two images so they can be stitched together or the motion of the imager between images can be estimated.  Motion estimation is particularly useful to robotics as a way to estimate things like motion of your vehicle.

For this project we start by implementing a basic Harris corner feature detector and a simple 5x5 rectangular window descriptor. We implement a more sophisticated feature descriptor that is less susceptible to error from rotation and scaling of the different images. To accomplish this we implemented the features from the Speeded Up Robust Features [1] (SURF) paper found here. These features can be scale invariant but for that to be true we must look for features at multiple scales so we also implemented the feature detector described in the paper.  Finally we run benchmarks and compare the results from the basic detector/feature combination, our multi-scale detector and SURF features, and the SIFT results provided for this project.

Harris Corners

The Harris corner detector works by taking horizontal and vertical derivatives of the image and looking for areas where both are high, this is quantified by the Harris corner descriptor which is defined in our case as the matrix  and the descriptor is . We define a feature as a point that is a local maximum on a 3x3 area and is above a threshold that is found through experimentation.

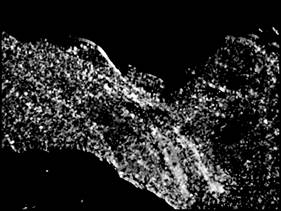
Figure 1. Example image from the Yosemite data set (left) with Harris values (right) shown.

Figure 2. Example image from the Graffiti data set with Harris values show on the right.

SURF

The SURF feature detector works by applying an approximate Gaussian second derivative mask to an image at many scales.  Because the feature detector applies masks along each axis and at 45 deg to the axis it is more robust to rotation than the Harris corner.  The method is very fast because of the use of an integral image where the value of a pixel (x,y) is the sum of all values in the rectangle defined by the origin and (x,y).  In such an image the sum of the pixels within a rectangle of any size in a source image can be found as the result of 4 operations.  This allows a rectangular mask of any size to be applied with very little computing time.

To detect features we assemble the Hessian matrix  where is the convolution of the second derivative of a Gaussian with the image at the point.  The masks used are a very crude approximation and are shown in Figure 3.  The crude approximations are valuable because they can be very quickly run at any scale due to the use of an integral image.

The Hessian determinate values for the same image as Figure 3 are shown in Figure 4 for the range of detector windows that were used in this work.  Valid features are found as a local maxima over a 3x3x3 range where the third dimension is detector window size, so a feature must be locally unique over a spatial range and a range of scales.  The SURF authors used a fast search algorithm to do non-maximum suppression, we have not implemented this yet.

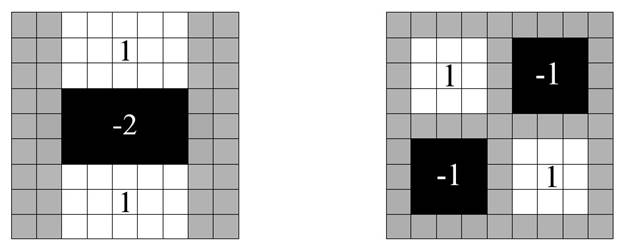
Figure 3. Approximated Gaussian second derivative used for the SURF detector.  This detector works well with integral images because only the sum over a rectangle is needed. On the left is the mask used for GXX and GYY and on the right is the mask used for GXY. Taken from the original SURF paper.

 

 

 

Figure 4. Surf feature values at 4 different detector sizes. Top Left = 9x9, top right = 15x15, bottom left = 21x21, bottom right = 27x27

Feature Descriptors

Having found features in the previous section we must now find some aspect of those features that can be compared among the features.  This is the descriptor.

Basic 5x5

We were assigned to implement a basic window descriptor which is the values of the 5x5 window of gray scale values centered on the feature we are describing.  This description is invariant to planar motion but fails if there are changes in lighting or rotation.

Surf Descriptor

The SURF descriptor is designed to be scale invariant and rotationally invariant.  To ignore scale the descriptor is sampled over a window that is proportional to the window size with which it was detected, that way if a scaled version of the feature is in another image the descriptor for that feature will be sampled over the same relative area.

Rotation is handled by finding the dominant direction of the feature and rotating the sampling window to align with that angle.  Once the rotated neighborhood is obtained it is divided up into 16 sub (A­i) squares, each sub square is again divided into 4 squares.  Derivatives in the x and y directions are taken in these final squares.  The descriptor for the sub square (A­i) is the sum of the x derivatives over its four quadrants, sum of the absolute values of the x derivatives and similarly for y.  The total descriptor is 4 values per (A­i) for a total of 64 values.  This vector is normalized to length 1 and is the feature descriptor.  The process is summarized in Figure 5.

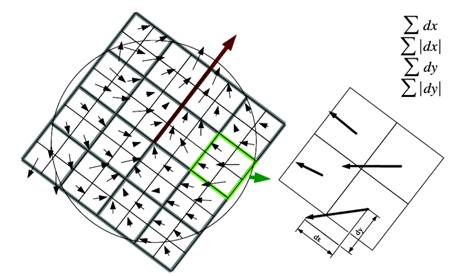
Figure 5. A graphical representation of the SURF descriptor.  This figure taken from the original SURF paper.

There are a few aspects of the SURF detector and descriptor that we have not yet had time to implement.  First creating the features is a very slow process, no optimization has been done yet on this step. The SURF authors include a Gaussian weighting over the descriptor and a more efficient matching system we have not implemented these yet.  Currently our best performance is with the sum-squared-distance matching system but it ignores a lot of information that is available. An additional problem is shown in Figure 6, we haven’t created a good way of dealing with borders yet so we avoid them.  This leads to ignoring potential features near the edges of the image.

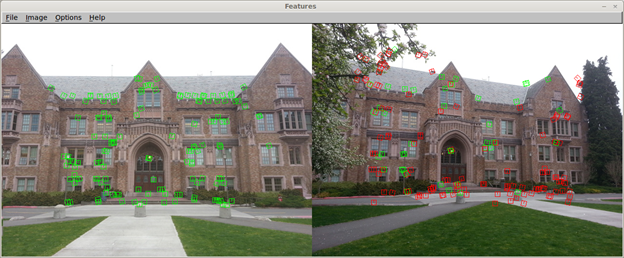
Figure 6. Matched features of Guggenheim Hall in a rotated image.  Clearly there is room for improvement.

Comparison

We ran a comparison on 4 sets of benchmark images that were provided with the project, the results are shown in Table 1.  From the data we can see that the Harris features with square descriptor work much better with the Ratio match than with the sum-square-distance metric.  The SURF feature with SURF descriptor however works much better with the sum-square-distance metric.  The SURF features also significantly outperform the Harris type.

Table 1. Results from benchmark image sets, Bikes, Graffiti, etc. are the respective areas under the ROC curve, Run Time is over all four sets of images and should be considered a rough metric as no particular care was taken to ensure no other load on the computer while benchmarking and timing was only done to the system clock second level.

Feature Type

Match Type

Bikes

Graffiti

Leuven

Wall

Run Time (s)

Harris

SSD

0.381

0.617

0.106

0.208

26

Harris

Ratio

0.513

0.517

0.474

0.565

25

SURF

SSD

0.775

0.682

0.767

0.638

121

SURF

Ratio

0.734

0.510

0.691

0.600

121

 

The image set that caused the most trouble was the Wall set because it includes a lot of areas that locally look like features but globally could fit nearly anywhere in the image.  An  example is shown in Figure 7.

The second comparison was done against the SIFT detector comparing 2 images. The original images and the ROC curves for the comparisons are shown in Figure 8 and Figure 9.  The ROC curves show that the SURF descriptor works better than the Harris detector but not as well as the SIFT descriptor.  Some reasons for this are discussed in the SURF Descriptor section and in the conclusion.

Figure 7. Example from the wall data set. Notice that every area looks like every other area.

Figure 8. ROC curve from the comparison of Yosemite1 and Yosemite2 in the Yosemite data set. The SURF detector outperforms the MOPS but not the SIFT. The comparison images are above.

 

Figure 9. ROC curve from comparison of img1 and img2 in the Graffiti data set.  The SURF detector outperforms the MOPS but not the SIFT. The comparison images are above.

Conclusion

Our implementation of the SURF detector/descriptor significantly outperformed the base implementation of the Harris detector with square descriptor.  We came much closer to the performance of SIFT. According to the authors of the SURF detector it should outperform SIFT in many cases our failure to perform at that level is most likely due to coding errors and the omission of Gaussian masks in a couple of different places.

Our implementation of SURF also runs very slowly.  The detection step is quite fast but calculating the descriptors takes a very long time.  Also many more features pass the thresh set the larger the detector window we use, this is clearly a bug and could probably be fixed by some type of normalization.  We took the SURF authors suggestion to normalize by the window size but that did not completely fix the problem.

In conclusion we have implemented a Harris feature detector, a square patch feature descriptor, and a SURF feature descriptor, in completion of the assignment. As extra credit I have implemented a SURF feature detector which was necessary for the SURF descriptor.

 

Bibliography

[1]

H. Bay, T. Tuytelaars and L. Van Gool, "SURF: Speeded Up Robust Features," in Computer Vision - ECCV 2006, Graz, Austria, 2006.