CSE 576
Computer Vision
Project 1:
Feature Detection and Matching
Mengyuan Liu
liumyzoe@uw.edu
April 18, 2013
Introduction
In this project, I
developed a set of algorithm for feature detector, feature descriptor and
feature matching to identity discriminating features from an image and search
for matching features in other images. Especially, my implementation was
designed to detect features that are reasonably invariant to translation,
rotation, illumination and some scaling.
Methods
Feature Detector
For the feature detector, I tried two implementations of Harris Operator as described in class and textbook.
For the simple implementation:
á Smooth the image with a Gaussian kernel (sigma =1)
á Calculate the gradient of each pixel with kernel [-1 0 1] (in x direction) and [-1 0 1]T (in y direction)
á For each pixel in the given image, computer the Harris Matrix H as a weighted summation of all pixel in the 5*5 detector window.
á Compute corner strength function for each pixel c(H) = det(H)/tr(H).
á Select pixels as features of interest if its corner strength is local maxima in a 3*3 neighborhood above certain threshold.
á Output the features of interest to further descriptor.
For the more detailed implementation: (from textbook page 214)
á Compute the horizontal and vertical derivative of the image by convolving the original image with derivatives of Gaussians, which is 3*3 Sobel kernel. (This step is same with first smooth the image with 3*3 Gaussian kernel, then compute the gradient.)
á Compute the Ix2, Iy2, and IxIy image corresponding to the outer products of these gradients. These 3 images are the entries of Harris matrix H of all pixels.
á Convolve each of these images with a 7*7 Gaussian. This step equals computing Gaussian weighted summation of Ix2, Iy2, and IxIy respectively within a 7*7 window.
á Compute corner strength function for each pixel c(H) = det(H)/tr(H).
á Select pixels as features of interest if its corner strength is local maxima in a 3*3 neighborhood above certain threshold.
á Output the features of interest to further descriptor.
Feature Descriptor
For the feature descriptor, I tried two different descriptors.
For the simple descriptor:
á 5*5 window around the given feature was used as feature descriptor.
á Followed by normalization to account to illumination variance.
á This descriptor should achieve illumination and translation invariant.
For the more advanced descriptor, which adds rotation invariant:
á Given a detected feature, its dominant orientation was computed from the smoothed local gradient. The dominant orientation was divided into 8 bins.
á Take a 41*41 patch around the detected feature and rotate the patch towards its dominant orientation. The pixel value after rotation was calculated through bilinear interpolation.
á Normalize within the 41*41 patch.
á Down sample the 41*41 patch to 9*9 patch.
á Use this 9*9 patch to be a 81-element feature descriptor.
Feature Matching
After feature detection and description, feature matching was realized through two methods: SSD (given in skeleton code) and ratio SSD test. For the ratio SSD matching, the ratio between nearest SSD and the second nearest SSD was used as the matching score between two features from two images. By doing this, some ambiguous matches, especially in cases when images contain a lot of repetitive patterns or similar features, could be excluded.
Results
ROC Curves (left: Yosemite; right: graf)
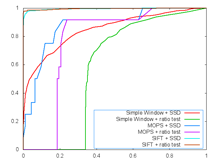
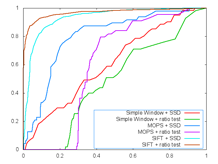
Images of Harris
Operator


Yosemite images: (left: Yosemite1; right: Yosemite2)
graf images: (left: graf1; right: graf2)


Average Error and AUC
for Benchmark Images
|
|
Window + SSD |
Window + ratio |
MOPS + SSD |
MOPS + ratio |
||||
|
|
AvgError |
AgeAUC |
AvgError |
AvgAUC |
AvgError |
AvgAUC |
AvgError |
AvgAUC |
|
Bike |
377.99 |
0.665 |
375.51 |
0.421 |
438.04 |
0.863 |
433.19 |
0.702 |
|
Graf |
301.05 |
0.445 |
297.73 |
0.402 |
300.09 |
0.500 |
298.04 |
0.432 |
|
Leuven |
316.62 |
0.788 |
292.13 |
0.565 |
311.18 |
0.762 |
291.33 |
0.600 |
|
wall |
322.46 |
0.671 |
310.35 |
0.487 |
379.17 |
0.621 |
373.57 |
0.498 |
Tests on Other Images
I also tested my algorithm on this following set of images. There are translation, illumination difference, a little scaling, and some rotation between these two images.


Feature detection and matching results are shown below. We can see that performances of illumination invariance, illustration invariance and rotation invariance (not much rotation between two images) are satisfactory. And small amount of scale invariance is achieved, too.

Discussion
My approach includes three components that handle rotation invariance, illumination invariance, and translation invariance. Translation invariance is achieved by comparison to all features in the to-be-matched image. Illumination invariance is realized by, for each patch, subtracting mean within the patch and divided by the standard deviation of the patch. Rotation invariance is achieved by computing each patchÕs dominant orientation and rotate all patches by this degree before comparing to other features.
Ratio matching mainly improves performance when a lot of repeats or many similar features existing in the image. However, most of the images donÕt have these. Therefore, the average AUC, which generally speaking is an indicator of True Positives versus False Positives may not reflect great improvement. However, the improvement could be clearly seen in average number of errors of matching when compared to the ground truth. The results above were generated with ratio threshold of 0.97, which is very high. If we adjust this threshold lower, more obvious improvement in average error would reveal.