Abstract

In this project several interesting steps of feature dection and maching was implemented. These steps including a Harris feature descriptor, image piramid to help obtaining scale/resolution invariance, and a gradientfeature descriptor. The results were then tested on several set of benchmark images. This method was then evaluated with ROC plots on its maching results and compared with other popular methods.


Introduction

Feature detection and matching has various important applications on computer vision such as object tracking, image stitching and 3D reconstruction. Its performance, accuracy and robustness are usually the bottlenecks for computer vision systems and thus it is a topic with extensive research effort. This project is an attempt trying to engineer a good feature detector/descriptor with known knowledge.

Design highlights

Design choice reasoning
1 Feature detection pyramid Increased scale and resolution invariance change
2 Exclusion of clustered features reduced rate of false negative errors
3 5x5 differential descriptors Increased lighting condition invariance


Design Specification

The algorithm for feature generation is summarized below:

  1. Convert the image to grayscale
  2. Construct a level 5 pyramid based on the grayscale image, each level of the pyramid is the previous level convolved with a 5x5 gaussian kernel, and downsized by 2.
  3. Compute Harris value for each point in each image of the pyramid using
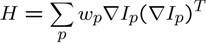
    banner logo
    where w is also a 5x5 gaussian kernel. The Harris is computed with the lower eigenvalue as abs((h11 + h22 - sqrt(4*h12*h21 + (h11-h22)*(h11-h22))))
  4. Compute local Maxima using a 3x3 window, if there are more than one maxima in one area, the pair as a whole are eliminated as they would add randomness to the features
  5. push the maxima as features, the descriptor is just the differential values on a 5x5 window sampled around the feature point, this window, again, was convolved by the 5x5 gaussian kernel to give circular weights
  6. Machtching is done comparing the Euclidean distance between feature sets or the ratio between the best and the second best.


Software Implementation

The algorithm was implemented in C++ on the skeleton code provided by the course. Relevant libraries were provided by Richard Szeliski in 2001. Aside from having various linker problems instantiation of template functions in my compiler, a good amount of minor details were modified in the library to ensure accurate result. The convolution routine was implemented using its definition and not optimized via Fast Fourier Transform. As most of computing were convolutions in this project, a FFT implementation of covolution could further improve algorithm performance


Results and evaluation


1.benmark test with 5x5 window descriptor, euclidean distance matching score
DataSet Averaged AUC Averaged error
bikes 0.763074 351.818781 pixels
graf 0.556292 294.190016 pixels
leuven 0.289110 394.819402 pixels
wall 0.379246 367.744664 pixels

2.benmark test with 5x5 window descriptor, ratio euclidean distance matching score
DataSet Averaged AUC Averaged error
bikes 0.758166 351.844164 pixels
graf 0.536326 294.361374 pixels
leuven 0.512425 394.666906 pixels
wall 0.637607 367.781199 pixels

3.benmark test with gradient window descriptor, euclidean distance matching score
DataSet Averaged AUC Averaged error
bikes 0.743449 310.657573 pixels
graf 0.537948 302.726848 pixels
leuven 0.594175 279.365569 pixels
wall 0.653070 315.959649 pixels

4.benmark test with gradient window descriptor, ratio euclidean distance matching score
(best results)
DataSet Averaged AUC Averaged error
bikes 0.804462 311.124159 pixels
graf 0.551508 302.692983 pixels
leuven 0.797392 279.235992 pixels
wall 0.784871 315.939953 pixels


fig.1 harris function for graf

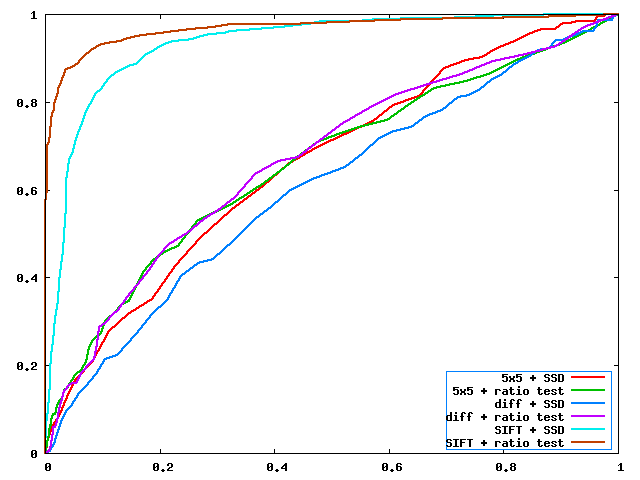
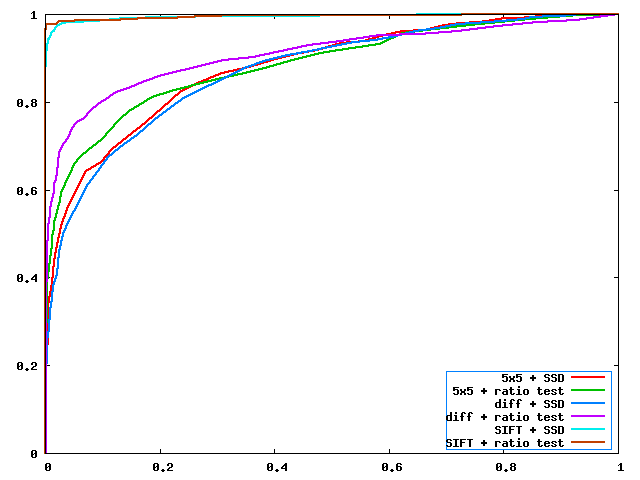
banner logo



fig.2 harris function for yosemite

banner logo



fig.3 6 roc plots for graf

banner logo



fig.4 6 roc plots for yosemite

banner logo




Conclusion and discussion

Observing results from different testbench images, I conclude that after applying gradient window descriptor, images sets with differences in illumination saw really good performance boost. This is is because the gaussian kernel acts as a low frequency filter and the gradient filtered out the DC component of the patch(illumination change invariant). Applying the ratio SSD matching increases the results in general as it takes out a good number of false posible results. However, the algorithm in general is not rotation transform invariant so that the performance is pool images with rotations.


References

Szeliski, Richard. Computer Vision: Algorithms and Applications. London: Springer, 2011. Print.