CSE 576 Project 1:
Feature Detection and Matching
eehmchen at u dot washington dot edu
April 18, 2013
Feature Detection
Multi-Scale Pyramid[1] (Extra Credit)
To make the feature more invariant to scale, a pyramid of images with different scales can be utilized. In this project, I create this pyramid of images of 5 levels as follows:- Filter the low level image (level l) with a Gaussian kernel ([1 4 6 4 1]/16 in separable two dimensions).
- Downsample the blurred image and save it as the up level image (level l+1).
- Repeat process 1 and 2 until get a 5 level (level 0-4) of pyramid.
Harris Corners
Given a image at level l, the first step is to find interest points in the image. For every point in the image. A Harris matrix can be generated as follow [1]:
The "corner" strength function is
Followings are Harris image for Yosemite and graf:
Adaptive Non-Maximal Suppression[1] (Extra Credit)
After calculating the Harris value, what we want are the points with the largest value, which means it is more likely to be a corner. One method is to set a threshold and select the points with value larger than it. However, it is not easy to choose a proper threshold adaptively and the selected points may have many overlap. Instead of setting a threshold for the whole image, the Adaptive Non-Maximal Suppression algorithm can select the interest points with better spatial distribution.
The main idea of this method is to select the point which is maximum over a large area. A minimum suppression radius $r_i$ calculated to measure the area, as:
where $x_i$ is a 2D interest point image location and $\mathcal{I}$ is the set of all interest point locations. The value $c = 0.9$ is to ensure that neighbor must have significantly higher strength. In this project, we select the 500 interest points with largest values of $r_i$
The following figures compare the results of using regular detection (local maximum in the $3\times 3$ window and above a threshold) to the AMNS. It is obvious that features are distributed better across the whole image.
[back to top]Feature Descriptor
Rotation Invariant (Extra Credit)
Similar as discussed in the lecture sides, an orientation anlge θ=atan(dy⁄dx) could be derived. After getting the angle, I rotation the 40×40 window to the horizontal direction. After rotation, an 8×8 image patch is sampled with a stepsize of 5 in the 40×40 window. We use this 64 values as the descriptor vector
Contrast Invariant (Extra Credit)
After sampling, the descriptor vector should be normalized to make the features invariant to intensity. Finally, the feature vector will have zero mean and one standard deviation.
[back to top]Feature Matching
Two matching methods are evaluated in this project: sum of square difference (SSD) distance and ratio score. SSD is the summation of square differences between elements of the two descriptors. I implemented the other method called ratio test. The ratio score is the ratio of the best match SSD and the second best match SSD. A smaller ratio score means a better feature point.
[back to top]Performance
ROC curves for Yosemite and graf
Average AUC on 4 Benchmark Sets
SSD match| average error | average AUC | |
| bikes | 245.904784 | 0.635211 |
| graf | 289.679639 | 0.568391 |
| leuven | 262.119331 | 0.649965 |
| wall | 254.218998 | 0.533478 |
Ratio Match
| average error | average AUC | |
| bikes | 245.904784 | 0.899729 |
| graf | 289.679639 | 0.680809 |
| leuven | 262.119331 | 0.861150 |
| wall | 254.218998 | 0.746586 |
I also evaluate different scenarioes those are w/ and w/o the pyramid structure and ANMS to see whether they improve the performance.
Without Pyramid (extract 2000 points in original level, ratio match)
| average error | average AUC | |
| bikes | 304.108791 | 0.849347 |
| graf | 303.153780 | 0.698413 |
| leuven | 283.916442 | 0.836846 |
| wall | 315.313407 | 0.818150 |
We can see the the error increase for all 4 dataset and the for "bikes" and "leuven" the average AUC also drops.
Without AMNS (only 3×3 local maximum Harris value, ratio match)
| average error | average AUC | |
| bikes | 183.982601 | 0.889333 |
| graf | 239.170204 | 0.650636 |
| leuven | 264.051454 | 0.874434 |
| wall | 231.801160 | 0.739099 |
Discussion
According the experiments, we can see that the pyramid structure is efficient and the ANMS algorithm can work well. For the bikes dataset, some images are blurred, so the pyramid can improve much better. I found that with and without ANMS, the performace didn't change too much.However there are more work can do. When doing rotation, I just use the nearest neigbour. A interpolation can be used to improve the accuracy.
[back to top]
Extra Credit
All the refined implementations are from MOSP paper.- Bulit a Gaussian image pyramid and extract features from each level, scale invariant. (explained earlier)
- Implement adaptive non-maximum suppression. (explained earlier)
- Normalized the feature vector to make it contrast invariant. (explained earlier)
- Computer the orientation angle and rotate the feature to make it rotation invariant (explained earlier)
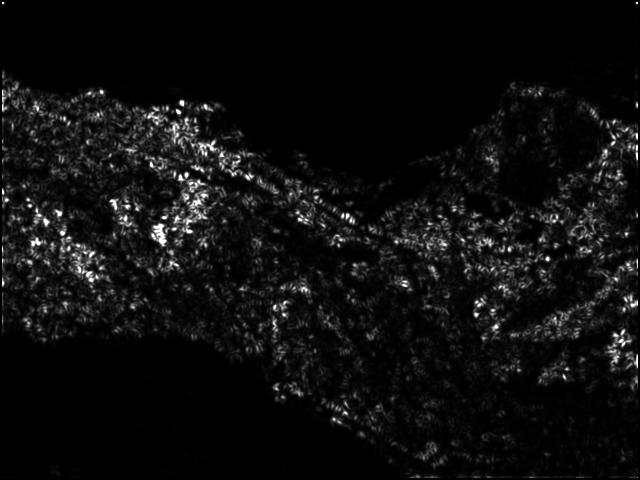 Harris Image of Yosemite
Harris Image of Yosemite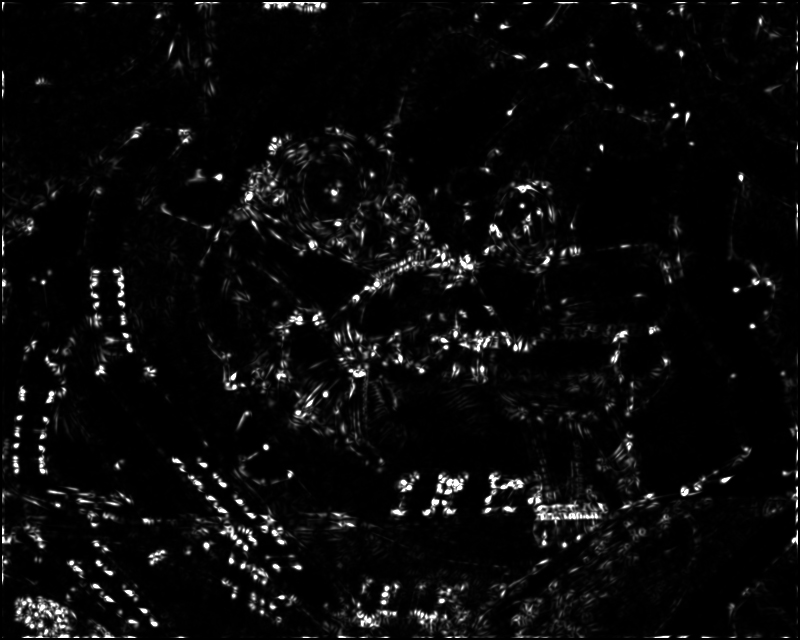 Harris Image of graf
Harris Image of graf Regular detection (maximum in local 3×3 window)
Regular detection (maximum in local 3×3 window)  Adaptive Non-Maximal Suppression
Adaptive Non-Maximal Suppression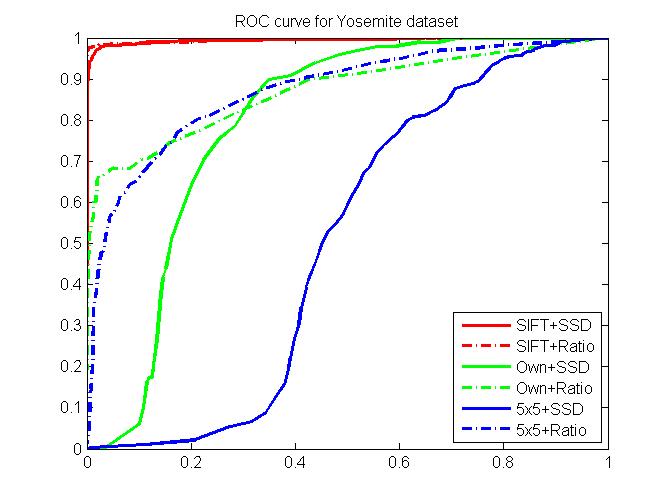 ROC curves for Yosemite
ROC curves for Yosemite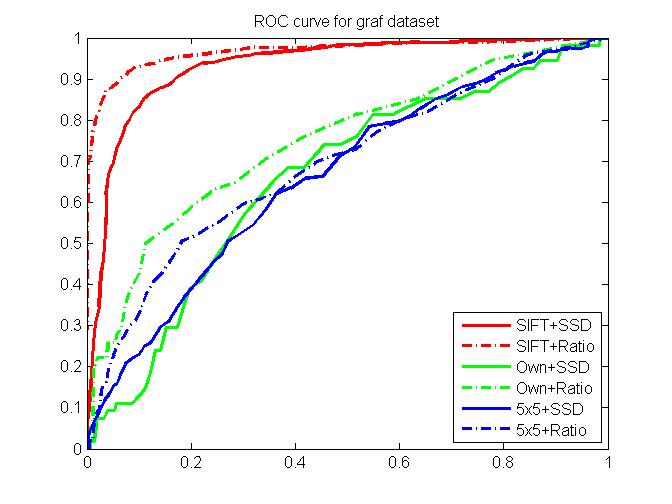 ROC curves for graf
ROC curves for graf