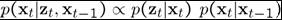Probabilistic Tracking
Treat
tracking problem as a Markov process
•Estimate
p(xt | zt, xt-1)
–prob of being
in state xt given measurement
zt and previous
state xt-1
•Combine Markov
assumption with Bayes Rule
prediction
(based on
previous
frame and motion model)

measurement likelihood
(likelihood of seeing
this measurement)
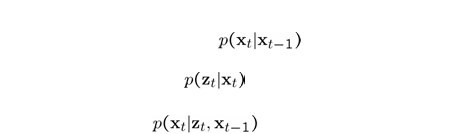
Approach
•Predict position at time t:
•Measure (perform correlation search or Lukas-Kanade) and compute likelihood
•Combine to obtain (unnormalized) state probability