We developed an animation interface to physical-based modeling of a blast wave impact on surrounding objects. We started with the "Animating Exploding Objects" paper from Graphics Interface 1999 (Mazarak et. al). This paper uses a connected voxel representation of objects to model explosions that result in solid debris. We coined the term "polyvoxel" to refer to a connected voxel object. When an explosion occurs, a blast wave travels through the scene. Each polyvoxel has internal links connecting the voxels. Whenever the pressure exerted by the blast wave is higher than the internal link, the link is broken. If there are no links connecting two or more parts of a polyvoxel, the polyvoxel will be broken into mutiple polyvoxels. Finally to each polyvoxel in the scene a blast force and a torque is applied and their motions are computed using rigid body mechanics.
Blast Wave Pressure Profile
The pressure profile generated by an ideal blast wave at some location can be accurately described by the Friendlander equation. There are three distinct phases through which an object passes when an explosion occurs:- (1) The pressure acting on the object is the atmospheric pressure.
- (2) When the blast wave first reaches the object, the pressure rises suddenly to an absolute maximum called the peak overpressure.
- (3) The pressure drops to a partial vacuum.
- (4) The pressure comes back to the atmospheric normals.

- p0 is the atmospheric pressure;
- Ps+ is the peak overpressure - that is the difference between the peak value of the explosion and the atmospheric pressure;
- t is the time measured from the time of arrival of the blast wave;
- T+ is the positive phase - the time in which the pressure of the blast decays to atmospheric pressure;
- b is a parameter related to the negative phase - the time in which the pressure drops to a partial vacuum and reaches back the atmospheric value;
- p0=100,000 Pa
- Ps=100 Pa
- T=1 s
- b=1
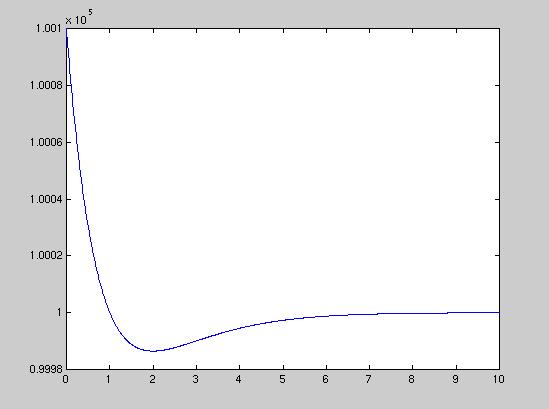
Figure 1 Plot of Friedlander Equation
Simulated Fracture
In order to simulate fractures of objects due to explosions, some notion of connectivity of an object must be incorporated in the models. We decided each object in a scene to be represented by a collection of voxels. We therefore refer to an object as a "polyvoxel". In addition to a list of voxels, polyvoxels contains a list of tensions between adjacent voxels. We chose to model objects using polyvoxels over polymeshes due to their volumetric and spatial properties.Whenever a polyvoxel is constructed, tensions between adjacent voxels are created. We chose to use a simple model of creating random tension strengths, by perturbing a random value generated within a certain range around some mean value:
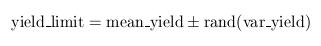
 (a) Building Initially |
 (b) Blast Reaches Building |
 (c) Windows Destroyed |
 (d) Floors and Roof Destroyed |
 (e) Building Collapsed |
Rigid Body Mechanics
In order to have the exploding chunks rotate correctly, we had to implement rigid body dynamics using polyvoxels. When the initial shape is created, we calculate the inertia tensor and the center of mass for the polyvoxel. We invert the inertia tensor and store the result. As the object turns, we can quickly calculate the inverse of the new inertia tensor for the current rotation as RI-1RT. However, if the polymesh splits, we must recalculate the inertia tensor and center of mass for the new pieces.In the work by Mazarak et. al., collision detection is done between each polyvoxel. However, this creates an enormous computational burden. In our early simulations, we found that when debris is flying around, you often can't tell visually whether collisions are happening or not. To keep things simple, we just checked for collisions with the ground plane, and applied appropriate reactive forces and torques.
Innovations
- When choosing the initial tensions between adjacent polyvoxels, we modify the strength according to the material that the voxels represent. This way we can make glass shatter more easily than concrete, for example. We also weaken the tensions between voxels of differing materials, which gives a more realistic splitting behavior.
- If the force of an explosion is not sufficient to break two adjacent voxels apart, we weaken the tension between them according to the applied pressure. This way they are more likely to be broken by later pressures.
- The algorithm presented by Mazarak et. al. resulted in very symmetrical explosions. To fix this, we introduced small random perturbations into the velocities of the debris.
Drawbacks
- In order to have a nice looking model, you need to use a lot of voxels. This slows things down a lot. Also, voxel models suffer from the problem that all of the faces on the object face in one of six directions, and so it is impossible to have smooth shading.
- Because of the architecture of our animation system, we could not easily implement adaptive timesteps. This means that unless the timestep is really small, objects will have to actually penetrate before we notice a collision. This result of this is particles that seem to vibrate around ground level, rather than coming to rest.
Movies
- Movie 1
Random building on a nice sunny afternoon. By mistake, somebody detonates a grenade. - Movie 2
Random Building on a nice sunny afternoon. By mistake, somebody detonates a bomb. - Movie 3
Random Building on a nice sunny afternoon. By mistake, a nuke is dropped.
Reference Papers:
- Animating Exploding Objects,
Oleg Mazarak, Claude Martins, John Amanatides, Graphics Interface 1999
- Explosing in Air,
Baker, W.E. University of Texas Press 1973
