CSE 544 Homework 4
1. [40 points total ] The HomeWotron disk has the following characteristics:
· 8 platters with 16 surfaces
· 2 12 = 4096 tracks per surface
· 2 9 = 512 sectors per track; there are no gaps between sectors
· 2 9 = 512 bytes per sector
· The disk rotates at 3000 rpm
· The head moves uniformly traveling 200 cylinders per millisecond (the start and stop times are negligible)
· 1 block has 4096 bytes
Compute the following:
a. [5 points] What is the disk’s capacity, expressed in Giga bytes (GB)? What is the maximum transfer rate, expressed in mega bytes per second (MB/s) ?
b. [5 points] Recall that the time needed to read a block of data consists of the seek time, the rotational latency, and the transfer time. Compute the transfer time for one block. Compute the average rotational latency. Your result should consist of two numbers, both expressed in milliseconds (ms).
c. [5 points] Assume cylinders are numbered 0, 1, …, 4095. Compute the seek time for a block on cylinder 1500 assuming that the head is positioned on cylinder 500 when the read command is issued. Your result should be a number, expressed in milliseconds.
d. [16 points] Generalize the result above: compute the seek time for a block on cylinder x, assuming that the head is positioned on cylinder y when the read command is issued. Your answer should be a mathematical function s(x,y), where both x and y are number between 0 and 4095 (it is OK to use if-then-else in a mathematical function: s(x,y) can be expressed using an if-then-else, but can also be expressed without one). Note: to verify that your result is correct, compute s(1500,500): it should return the same number you gave at point c.
e. [9 points] Compute the average seek time. For that, assume that both the block’s position x and the head’s initial position y are random numbers, uniformly distributed in {0, 1, …, 4095}. Your result should be a number, expressed in milliseconds.
f. [10 points extra credit] The HomeWotron SX is the top of the line model: it comes with two heads instead of one. The heads can move independently. When a read command is issued, any of the two heads can be chosen to read the block. The HomeWotron SX controller can be configured in one of two modes. In the NonPartitioned mode, the head closest to the cylinder where the block is positioned is chosen to read the block. In the Partitioned mode, head 1 is used to read cylinders 0, …, M/2, while head 2 is used to read cylinders M/2+1,…,M-1 (where M is the number of cylinders, M=4096 in our case). If your goal is to minimize average seek time, assuming uniform distribution both for the block position and the heads’ positions, which of the two modes would you choose? Your answer should consist of two mathematical formulas showing the average seek time for both modes, and an indication which is smaller. (Hints. Work with M rather than 4096. Use integrals rather than summations: integrals are approximations, but are easier to work with.)
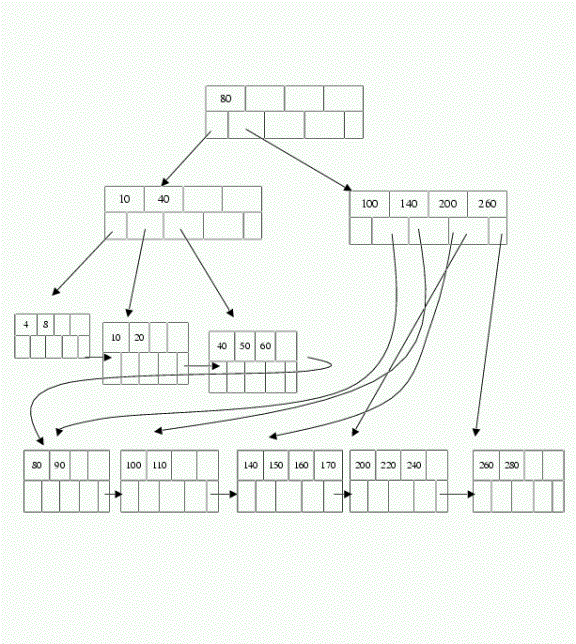
2. [25 points] Consider the B+ tree of order d=2 (i.e. each internal node has between 2 and 4 keys) represented here or below. Show the tree after each of the following operations:
a. Insert the key 70.
b. Insert the key 155.
c. Insert the key 165.
d. Delete the key 10.
e. Delete
the key 8.
Your answer should show five B+ trees. Notice: each operation is applied to the tree resulting from the previous operation. That is, your answer in e. should represent the tree with 70, 155, and 165 inserted and 10 and 8 deleted.
3. [35
points] Suppose keys in an extensible hash table are hashed to four-bit
sequences, and that each block can hold two records. We start with a hash table
with a single entry pointing to one empty block.
a. [5 points] Show the hash table after we insert records with keys 0000, 0001, 0010, 0011 ... 1111, in that order.
b. [5 points] Every time we copy a key from one block to another block we have
to pay $1. How much did we have to pay for the insertions at point a.
c. [5 points] Consider inserting the keys at point a in a different order.
Among all possible orders, which would require us to pay the most amount of
money ? How much do we have to pay in this case ?
d. [10 points] Generalize the above. Assume keys are hashed to k-bit sequences,
that each block can hold two records, and that we insert all keys 0...00,
0..01, …, 1…11 into the empty table, in some order. What is the cheapest order,
i.e. that require us to pay the minimum amount of money, and how much do we
have to pay in this case ? What is the most expensive order, and how much does
it cost ?
e. [10 points] Returning to the case of four-bit keys, start from a hash table
with a single entry pointing to one empty block and consider inserting the
following five keys 0000, 0001, 0010, 0011, 0100. How many entries does the
hash table have ? Generalize: assume keys to have k-bits, and blocks to hold
two keys. What is the minimum number of keys we need to insert to force the
hash table to have 2k entries ?