Lecture 14

Hidden Markov Model

December 4

Lecturer: Larry Ruzzo

Notes: Zizhen Yao

Recall from last time, in weight matrix method, we assume independent probability of letters occurring at each position, and fixed sequence length. To capture the dependence among positions, we need more sophisticated model. Markov and Hidden Markov Models are the ones widely used.

CpG island prediction.

Let’s look at an interesting biology problem first. As result of methylation, in general, CpG dinucleotides are rarer in the genome than would be expected from the independent probability of C and G. In some region of genome, such as around the promoters or ‘start’ regions of many gene, we see many more CpG dinucleotides than elsewhere, and in fact more C and G nucleotides in general. The question we are interested in are:

1. Given a short stretch of genome sequence, how would we decide if it comes from a CpG island or not?

2. Given a long piece of sequence, how would we find the CpG islands in it, if there are any?

Markov Model

In Markov model, the probability of a state depends only on previous state. The model is characterized by the paramters

a_st=P( x_i=t |x_i-1=s)

A Markov model (first order) generating DNA sequence look like this:

B: beginning state.

e: ending state

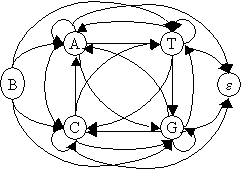
People also use higher order Markov model, in which a state depends only on last few previous states.

To solve CpG island problem, we can create two Markov models: one for CpG island, and one for non-CpG island, each has different transition probabilities on edges. And we compute which one of them is more likely to produce the given DNA sequence.

Given the Markov model, the probability to generate an output string is

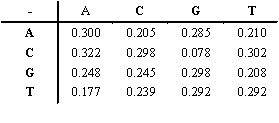The transition probabilities are specified in the table below.

The log-odds ratio is given as follows:

Declare some threshold for this ratio. If the S(x) is above the threshold, then it is CpG island, otherwise not.

However, this approach is unable to answer the second the question: how to pick up the islands from a long sequence. We could just compute the statistics for all lengths of , say, 500 bases, but this won’t give us sharp boundaries. In this case, we need Hidden Markov Model.

Hidden Markov Model:

We can combine the above two models (+, -) , such every state in + model (except the beginning and end state) has an edge to every state in – model ( except the beginning and end) and vice versa. Now there are two states corresponding to each nucleotide symbol. A+, C+, G+, T+ emit A, C, G, T respectively in CpG island regions, and A-, C-, G-, T - correspondingly in non-island regions. There is on longer a one-to-one correspondence between the states and the symbols. We cannot tell what state the model was by looking at the symbol at that position. That is why it is referred to as Hidden Markov Model.

Following is another interesting application of Hidden Markov Model:

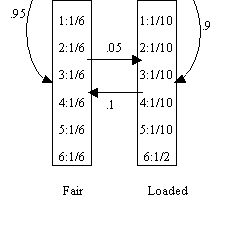
Occasionally dishonest Casino dice: a Casino uses loaded dice occasionally, while most of the time using fair dice. The transition graph of fair and loaded state is given below, with emission probability in the box.

We are interested to know, given a sequence of throw data, can we tell when a fair dice is used, and when a loaded dice is used? In general, a related question is “given the observed data, what is the most likely path through the model?”

Viterbi

Viterbi algorithm provides solution to the above question. It computes a sequence of state

given the transition probability and the emission probability .

The algorithm uses dynamic programming to compute the probability of the most probable path ending in state k with observation i, for each k and i. Let it be .

The recursive relation is:

The details of the algorithm will be discussed next time. We can predict the state given an observation i, by checking the state at the corresponding position in the most probable path.