CSE503: Software
Engineering
Lecture 11 (January 29, 1999)
David Notkin
v
An
alternative formulation to Hoare triples is to use Dijkstra's weakest
precondition predicate transformers that, in essence, provide a functional
approach to handling the predicates
Ø
wp(Q,S) is
defined to be the weakest logical predicate that must be true before executing
S in order to prove that postcondition Q is true afterwards
Ø
Ex:
§
wp(x > 10,x:=x+1)
= x > 9
§
wp(Q,skip) =
Q
§
wp(Q,S1;S2) =
wp(wp(Q,S2),S1)
§
wp(Q, if C
then S1 else S2) = (wp(Q,S1) and C) or (wp(Q,S2) and not C)
Ø
In general,
there is a direct analogy between Hoare triples and wp proofs, although on the
whole, wp proofs seem a little more straightforward, as they seem to capture
the intuitive notion of backwards reasoning for proofs more effectively
v
The last
topic in this area of program verification that I want to cover is the basics
of how to verify abstract data types
Ø
The basic
idea here is that you have an abstract data type A (representing a stack, for
instance) and an implementation C of that data type.
Ø
How do you
prove that the C satisfies the specification provided by A?
Ø
The first
step is to have a precise definition of the ADT A
ADT Stack is
private s == <>
const maxSize;
Push(x) { precondition == !Full()
postcondition
== s' = s || <x> }
Pop() { precondition ==
!Empty()
postcondition
== s' = <s1..sN-1> }
Top(): int { precondition == !Empty()
postcondition
== Top = sN and s' = s }
Empty(): bool { postcondition == Empty = (s = <>)
and s' = s }
Full(): bool { postcondition == Full = (len(s) = maxSize
and s' = s }
end Stack
Ø
We also
define an invariant over the abstraction representations
§
In this case,
we might say that the abstract invariant is defined as
len(s) <= maxSize
Ø
We also have
a concrete implementation of the stack, perhaps using arrays to represent the
sequence
package stackImpl is
private int sArray[1..maxSize];
private int sTop := 0;
procedure sPush(int x) is
if !sFull then
sTop := sTop +1;
sArray[sTop] := x;
fi
end
procedure…
Ø
We also need
to define a concrete invariant, which in this case is
sTop <= maxSize
Ø
In essence,
the abstraction, with its specification, describes how to map an abstract stack
to another abstract stack (perhaps with a return value of the operation)
Ø
And
similarly, the implementation, with its specification (which can be written in
Hoare triples or wp's), describes how to map a concrete stack to another
concrete stack
Ø
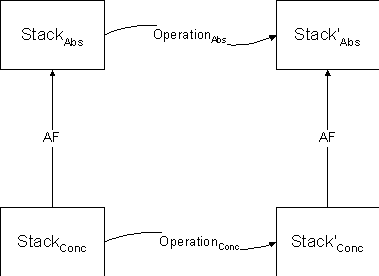
However, to
prove anything about the relationship between the abstraction and the
implementation requires an explicit abstraction
function (AF), which maps a state in the concrete implementation to a state
in the abstract representation.
§
That is, it
describes how to interpret a state in the concrete machine as a state in the
abstract machine
§
For the above
example, the abstraction function maps the [1..sTop] elements in sArray to a
sequence of elements in the stack's s variable
§
Note that many
different concrete states map to the same abstract state
·
sTop = 3 and
sArray = [1,2,3,4,5,6] and
sTop = 3 and sArray = [1,2,3,6,5,4] map to the same abstract state:
s = <1,2,3>
§
In general,
abstraction functions are many-to-one; this is one reason that the inverse
relation that maps abstract to concrete states is less useful in proofs
(although it seems sensible on the face of it)
Ø
This allows
us to think about the relationship between the two levels of abstraction, with
the basics captured in the figure at the end of the notes
Ø
Sketch of
proof technique
§
For each initial
concrete state i, show that AF(i) satisfies the abstract invariant
·
That is, make
sure that any initial concrete state is a legal abstract state
§
For each
operation of the concrete implementation and its associated abstract operation,
given a legal concrete state c, we need to show
opabs(AF(c)) = AF(opconc(c))
§
Essentially,
this is a proof by induction that shows that the concrete operations satisfy
the abstract operations
Ø
The basic
technique can be used to show satisfaction over any pairs of representations,
including state machines, different levels of specifications, etc.
v
OK, let's get
back to the question you asked last lecture: who cares about this?
Ø
I'd claim
that there are at least two reasons to understand at least the basics of
proving programs correct
§
It really
does provide a sound basis for understanding the relationship between
specifications and implementations, even if it is not realizable for sizeable
systems
§
When you are
writing or debugging your own code, or perhaps even TAing or helping someone
else with their code, it gives you an intellectual tool (which you can and will
and probably should use informally most of the time) to help
·
I don't think
about loop invariants in 99% of the loops I write, but when I am having a
problem, I often informally write down or at least determine what the loop
invariant should be, and this often helps
·
When debugging a system that uses
ADTs, the idea of separating out potential problems in (a) the abstract
definition, (b) the concrete implementation, and (c) the representation
function between them can be useful, too