CSE 473 - Artificial Intelligence - Spring 2014

Written Assignment 1: Markov Chains and Bayes Nets

Due Date: Due Wed May 28, 1:30pm in class or through the online dropbox.

Problem 1: Markov Chains [20 points]

Consider the following process. You can be employed or unemployed. At each time step, you have a 1% chance of loosing your job and a 15% chance of moving from unemployment to employment (finding a new job!). Unless otherwise specified, assume that you have a 50% chance of being employed at time 1.

A. [5pts] Model this employment process as a Markov chain.

B. [5pts] If you start out employed, what is the probability of being employed at step three? Show all of your work.

B. [5pts] If you are unemployed at time 3, what is the probability that you started out employed at time 1

C. [5pts] What is the stationary distribution of the chain you defined?

Problem 2: Bayesian Modeling [20 points]

Consider the following modeling challenge, which might arise when working on a homework problem. You can either study hard or trick the TA into telling you the right answer. Given these choices, you might actually learn the material and you might also get a passing grade on the problem. All of these possibilities will happen with certain probabilities, that you are welcome to imagine however you like.

A. [14pts] Model this problem as a Bayesian network representing a joint distribution over four binary random variables. Since there is more than one possible answer, briefly motivate your choices.

B. [6pts] Write three independence assumptions that your network encodes.

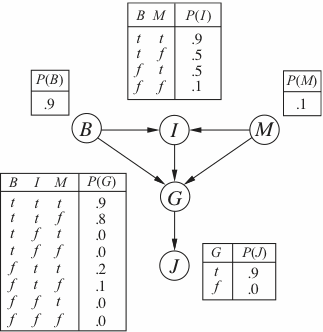
Problem 3: Bayesian Politics [15 points]

Consider the above Bayes net.

The variables are boolean and describe aspects of a court trail. They indicate whether someone broke an election law (B), was indicted (I), whether the prosecutor was politically motivated (M), if the person was found guilty (G), and if they were ultimately put in jail (J).

A. [9pts] Which of the following are true:

P(B,I,M) = P(B) P(I) P(M)
P(J|G) = P(J|G,I)
P(M|G,B,I) = P(M|G,B,I,J)

B. [3pts] What is P(b,i,¬m,g,j)?

C. [3pts] What is P(j,i,g | ¬m)?