CSE 473 - Artificial Intelligence - Spring 2013

Written Assignment 2: BN Inference, ML, and Logic

Due Date: Due Fri June 7 at 1:30pm in class or through the online dropbox.

Problem 1: Bayesian Review - Simple Spam [15 points]

According to extremely reliable sources (Wikipedia), 78% of email is spam. According to experiments conducted on my own inbox, 11% of spam email messages contain the word "Pills". In comparison, only 1% of non-spam email messages contain this word.

A. [5pts] What is the probability that a message contains the word "Pills" and is Spam?

B. [5pts] What is the probability that a message is Spam if it is known to contain the word "Pills"?

C. [5pts] What is the probability that a message does not contain the word "Pills" or is Spam?

Problem 2: Variable Elimination [25 points]

Consider the following Bayesian Network, with variables B, E, A, R, and W:


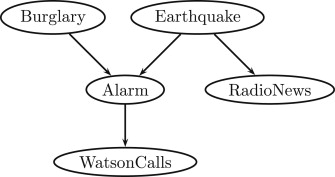
Consider computing the query P(B|W=true)

A. [5pt] Write the set of initial factors that would be created, after incorporating evidence. You do not need to write the full tables of numbers for each factor, just clearly indicate the function signature, e.g. P(X,Y,Z).
B. [10pt] Write, in order, the signatures for the new factors that get created when running the variable elimination algorithm with the variable elimination ordering A, E, R.
C. [5pt] Provide, if possible, a variable ordering that is more comptuationally efficient than the one in part B.
D. [5pt] Provide, if possible, a variable ordering that is less comptuationally efficient than the one in part B.

Problem 3: Naive Bayes vs. Perceptron [10 points]

A. [5pt] Describe a scenario in which you might prefer to use the Naive Bayes algorithm instead of the Perceptron. Be sure to specify any assumptions about number of features, amount of training data, smoothing techniques employed, etc.
B. [5pt] Similarly, describe a scenario in which the Percepton would be expected to perform better.

Problem 4: Propositional Logic [15 points]

For each of the following statements, state wether it is valid, satisfiable, unsatisfiable, or not a well formed formula in propositional logic.

A. [3pt] A ⇒ B
B. [3pt] ⇒ ¬ B
C. [3pt] A ∨ B ∨ ¬ B
D. [3pt] ¬ (A ⇒ A)
E. [3pt] ¬ A ∧ B ∧ (A ⇒ B)