CSE473 - Homework 1: CSPs & Logic

Due: Friday, May 4, 2012 at 6pm. In Dropbox. (If you want to turn in a hard copy, you must do so in class).

Problem 1: Constraint Satisfaction [14 points]

This problem comes in three parts, due Monday, Wednesday and Friday:

A. [4 pts, Due 9am Monday 4/30] Describing a puzzle as a constraint satisfaction problem.
Here are two puzzles which could be described as CSPs. You must write a description for the one assigned to you:

• Class scheduling [Do this if your student ID# is even]: There is a fixed number of professors and classrooms, a list of classes to be offered, and a list of possible time slots for classes. Each professor has a set of classes that he or she can teach.
• Hamiltonian tour [Do this if your student ID# is odd]: Given a network of cities connected by roads, choose an order to visit all cities in a country without repeating any.

To describe puzzles like these as a CSP, you need to list the variables, their domains and the constraints. Describe the CSP as clearly, precisely and completely as you can. You may turn in either a .txt file or a PDF.

B. [4 pts, Noon Wendesday 5/2] Providing feedback to another student about their answer to part A
On Monday, you'll receive an email with someone else's answer to part A. Can you see any ways to improve it? Provide detailed feedback to that person and turn in your comments by dropbox. (in .txt or PDF format)

C1. [4 pts, Due 6pm Friday 5/4] Revising your part A description based on the feedback you get from part B
When you get feedback on your answer to part A, revise your answer and turn it in via dropbox. (as a .txt file or PDF)

C2. [2 pts, Due 6pm Friday 5/4] Answer questions on a Catalyst survey (link coming soon).

Problem 2: CSP Algorithms [8 points]

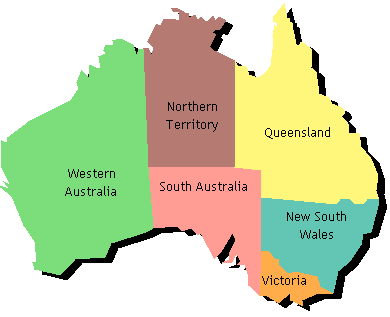Continental Australia may be thought of as having six states: WA, NT, SA, Q, NSW and V. Suppose each of them is trying to choose an official integer (kind of like a state flower, but more geeky). The Australian federal government has decreed that these integers must be between 1 and 9, so we can consider this choice to be a CSP with the six variables listed above each having the numbers in [1, 9] as domains. Alas, federal regulations constrain the choice of values further:

• Every state must have a unique number
• Every state must have a number larger than any state to the west of it (eg WA < SA).

Solve this CSP by perform arc consistency (eg the AC-3 algorithm in Figure 6.3 of the book) or another method of your choosing. Demonstrate how you arrived at your answer. Do any variables have an empty domain? If so, which ones? If not, write down the remaining values for each of the six variables.

Problem 3: Heuristic Admissibility [12 points]

Consider a search problem like the Romanian travel problem in the text book (eg Figure 3.2): nodes correspond to locations on a map and edge costs correspond to distances. Let n.x and n.y be the coordinates of state n and x* and y* be the coordinates of the goal. Which of the following are admissable heuristics?

A. [2 pts] h(n) = |x*-n.x| + |y*-n.y|

B. [2 pts] h(n) = min(|x*-n.x|,|y*-n.y|)

C. [2 pts] h(n) = max(|x*-n.x|,|y*-n.y|)

D. [2 pts] h(n) = calculate the shortest path distance from n to the goal in the original search graph.

E. [2 pts] h(n) = calculate the shortest path distance from n to the goal in a new graph, which is identical to the original graph except some additional edges have been added. (Clarification: you are still giving a heuristic on the original graph. We are not actually updating the original graph, just using information from a different, related graph to help inform h(n).)

F. [2 pts] h(n) = calculate the shortest path distance from n to the goal in a new graph, which is identical to the original graph except some edges have been removed. (Clarification: you are still giving a heuristic on the original graph. We are not actually updating the original graph, just using information from a different, related graph to help inform h(n).)

Problem 4: Propositional Logic [16 points]

Consider the following dinner-time dilemma:

• Bill wants pepperoni and/or sausage on the pizza
• Thomas wants sausage or olives but not both
• If the pizza does not have bacon, then Jill wants olives
• Bob wants bacon or pepperoni but not both
• If the pizza has olives, then Susan also wants tomatoes
• Jessica wants olives if the pizza has bacon.

Using the proposition P to denote that someone wants Pepperoni on the pizza (and S, O, B and T to denote sausage, olives, bacon and tomato respectively), encode the facts listed above in propositional logic and convert them to clausal form. Use the hash sign (#) to signify negation. Remember that clausal form is a list of lists. Each of the inner lists represents a clause (a disjunction) and all of the clauses in the outer list must be true (the outer list is a big conjunction)
Normalize each clause so that the individual literals are listed in alphabetic order with #P being ordered before P. Normalize the outer list of clauses so that they are ordered lexicographically with the left hand symbols being of higher importance. For example, if A, B, and C are propositions then the following clausal form would be correctly normalized
((#A, B), (#A, C), (A, B), (B, C))

A. [8 pts] What is the normalized clausal form for the pizza constraints above?

B. [2 pts] Is the formula satisfiable, unsatisfiable or valid?

C. [6 pts] Using resolution, prove that the pizza must have olives, pepperoni and tomatoes with nothing else. Write up your proof by first showing the clausal form of your KB with the negated goal and then, on successive lines show a sequence of deductiv steps leading to contradiction. For example, to show that ((#A, B), (A), (#B, C), (#C)) is inconsistent, one might write the following deductive steps:
(#A, B) + (#B, C) |- (#A, C)
(#A, C) + (A) |- (C)
(#C) + (C) |- ()