CSE 473 Sp 00 Homework 2 Due 5/12/00
Name: _______________________________________

Email: _____________________________________

Please show your work.

  1. Given the propositions:
    (I) (P&Q) -> R
    (II) R -> S
    (III) Q & ~S
    (IV) ~P
    1. Write the truth table for statement (I).
    2. Use the rules of logic in Figure 6.13 in the book (p. 172) to show that (IV) follows from (I), (II) and (III).
  2. You have the following predicates: HeadOf(h,x), Horse(x), Animal(x) Write the logical formula corresponding to the statement: "The head of a horse is the head of an animal" and "Horses are animals".
    1. Convert the statement into CNF.
    2. Prove that "The head of a horse is the head of an animal" follows from "Horses are animals" using resolution and the statements you have in part A.
  3. Assume the following facts:
    Steve only likes easy courses.
    Science courses are hard.
    All the courses in the basketweaving department are easy.
    BK101 is a basketweaving course.
    Susan likes the same courses as Steve.

    4. (a) Translate these sentences into predicate logic. (You will need to add commonsense axioms to make the proof possible, Also, there are several ways to represent "only likes"; find one that will work in the proof.)

    (b) Convert the formulas into CNF.

    (c) Prove that Steve likes BK101 by resolution (don't forget to negate the conclusion).

  4. Consider the following joint probability distribution:
    5.
      ABCD P
      TTTT 0.040
      TTTF 0.040
      TTFT 0.256
      TTFF 0.064
      TFTT 0.016
      TFTF 0.064
      TFFT 0.160
      TFFF 0.160
      ABCD P
      FTTT 0.010
      FTTF 0.010
      FTFT 0.016
      FTFF 0.004
      FFTT 0.016
      FFTF 0.064
      FFFT 0.040
      FFFF 0.040
    1. Determine P(A|D) and P(D |C,A).
    2. Construct a belief network equivalent to this distribution (Hint: A is parent of B and C, and C & B are parents of D)
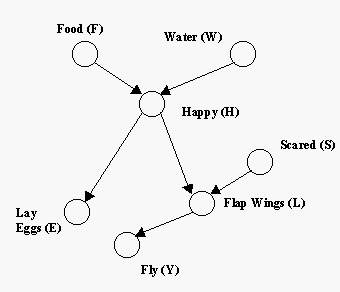
  5. The following diagram shows a Bayesian network representing the behavior of a domestic chicken. All variables are Boolean.
    1. Decomposes the joint probability P(Y, E, F, W, H, L, S) into a product of node probabilities using the network above. (A node probability is the probability of a node given its parents)
    2. Express the following probabilities in terms of the node probabilities:
      (I) P(Y | F, S)?
      (II) P (W | Y,E) ?
    3. What is the markov blanket for the event H?
    4. If we know the chicken is happy, are the following events independent?
      (I) F, W
      (II) E, L
      (III) W, Y