CSE 473 Sp 00 Homework 1 Due 4/17/00
Name: _______________________________________ Email: _____________________________________

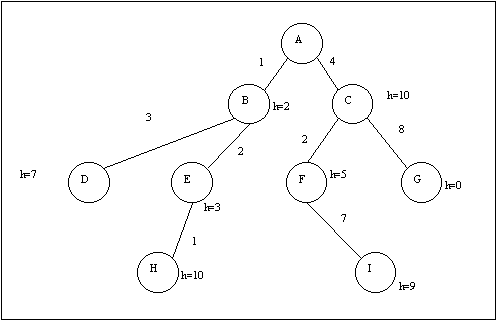
1. In the following search space, the number beside edges denotes the path cost between nodes, and h is the estimated path cost from the node to the goal state G.
1. Give the order by which the nodes are visited in an A* search of the space. Write down the f(n) for each node n.
2. Would greedy search do better? How many more or less nodes does it take greedy search to reach G?
3. Both breadth-first search and A* search takes exponential memory. How would you modify A* to use less space? What is the space complexity of your new algorithm?
4. If H is also a goal, which algorithms among breadth-first, depth-first and iterative-deepening would find the optimal solution?
5. (Bonus) The heuristic function h has a problem, it overestimates the cost from C to G. What property of A* search would be lost if h has this problem?

 



  

2. Consider the 8-puzzle problem, explain why the number of misplaced tiles and the Mahattan distance heuristics do not always make the best move. For each heuristic, give an example to support your explanation by drawing the original state of the 8-puzzle, and describe what move the heuristic chooses and what the optimal move is.
3. How would you implement best-first search if you can only tell if one node is better than the other, but not the exact cost (h(n))? Explain the differences, if any, of this algorithm.
4. In the classroom scheduling problem, we have c classrooms and k classes, each class starts at s_k ends at e_k, both of which are integers. No two classes shares the same classroom. Classrooms are only available from 1:00 to 4:00.
1. Formulate this problem into a CSP.
2. Suggest a heuristic for solving this CSP and explain why you think your heuristic would work.
5. Suppose you want to implement a program to play tic-tac-toe. The human player always use O and computer always use X. Each square on the board is labeled as a_ij where i is the row number and j is the column
1. Define the states, goal test, and operators for this problem in terms of a_ij. How many possible states are there?
2. What search algorithm would you use to implement the search? Why?
3. Briefly describe a function that evaluates the performance of the computer player given one of the states you defined in part A.