Ray Tracer Road Map
Useful links previous help sessions:
Survey of Standard Template Library (STL)
Overview
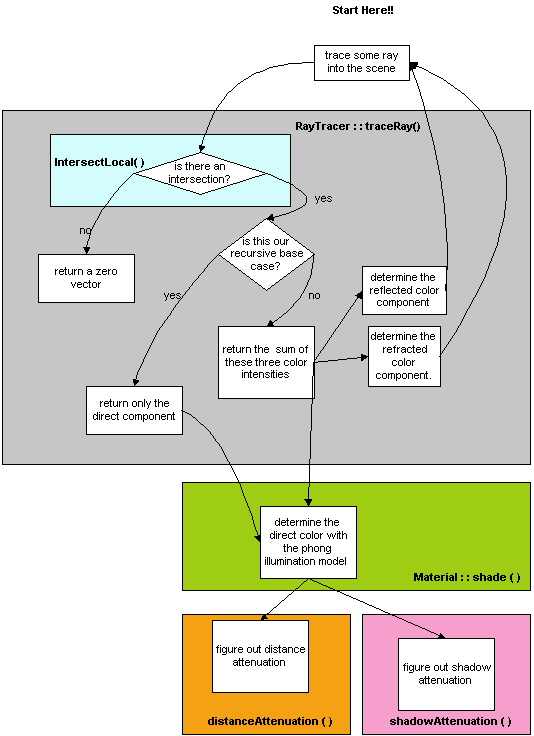
Recall how a raytracer functions, as described in class. The raytracer iterates through every pixel in the image, and, using some illumination model determines what color intensity is assigned to the pixel. The skeleton code goes through several functions to do this, but the real interest occurs when you get to the RayTracer::traceRay( ) function. This is also where a handy diagram can start to be of help (shown below). The diagram is supposed to represent the flow of the ray tracing program. Each separately colored box represents a different function that you will have to add some code to in order to finish the project.
The traceRay function takes three arguments: a ray that needs to be traced, a threshold vector, and an integer that controls the depth of recursion for the ray tracer. It returns a color (represented through a three-dimensional vector). The signature of this function should make its purpose clear: a ray is input to it, and the function determines the color that should be projected back to whatever it was that cast the ray. In order to do this, the first thing traceRay wants to know is if the ray actually hits anything that is worth looking at, or if it wanders off into the lonely darkness of space. This is where a test for ray/object intersection occurs (how intersection works is described below). If no intersection occurs, then a black color is returned (the zero vector). If an intersection occurs some work has to be done to figure out what the color is.

How the color is determined:
Before you try to code up a solution for the color model, be sure that you have a pretty good idea of how to do it on paper. Some of the vector math can start to look pretty overwhelming if you don't know what you are doing. Even when you do know what you are doing, their can be some rather tricky pitfalls... three different things contribute to the color of a certain object:
How Intersections work
Because ray/object intersections are typically the bottleneck of ray tracing programs, the skeleton code uses a few techniques to try to speed it up. If an objects position is described by a transformation M, then M inverse is applied to both the object and the ray. This transforms the object back to the origin, which simplifies intersection testing.
For each object, the intersection testing occurs in the objects intersectLocal function. By the time control has been given to this function, the object and ray have already been translated back to the origin, so you don't have to worry about doing that. Additionally, you don't have to worry about translating the object and ray back to their original position; this is done after the function exits. You only have to worry about the intersection of the input ray and the basic, untransformed object (i.e., untransformed spheres are centered at the origin with a radius of one ). If an intersection is found, then some information about the object needs to be calculated. The Normal and t-value for the intersection need to be properly set, so that the information can later be used to calculate lighting information. All of this information should be stored in the "i" argument that is passed by reference into intersectLocal.
Important classes
const
SceneObject *obj;
A pointer to the object intersected, in case you need to access
the object.
double
t;
This is the linear value from where the ray intersected the object.
In other words, if you wrote out the ray formula as [P + t*D] where
P is
the position of the ray and D is the direction, this t is the t in the formula.
You can use it to find the point in 3D space where the intersection took
place.
vec3
N;
This is the surface normal where the intersection happened.
const
Material &getMaterial() const;
And finally, this method gets the material properties of the surface at
the intersection. Itís just a
time-saver, using the intersectionís own material pointer if itís defined,
or getting the object material if not.
vec2f
uvParameters;
This should store the surface parametric coordinates of the intersection,
which will be used in the texture mapping stage to find the location in the
2-dimensional map. Should range
from 0 to 1. These really only need to be used
if you wish to do texture mapping.
vec3
ke();
Emmisive property
vec3
ka();
Ambient property
vec3
ks();
Specular property
vec3
kr();
Reflective property
vec3
kd();
Diffuse property
vec3
kt();
Transmissive property
double
shininess();
The shininess exponent when calculating specular highlights. NOTE: This is the "n_s" exponent from the Blinn-Phong shading equation.
double
index();
Index of refraction for use in forming transmitted rays.
Note that for each of these functions you must pass in an isect& since the functions may need the isect to figure out parametric coordinates of the intersection for 2D texture mapping, space coordinates for use with solid textures, etc.