Summary

Overall comments

The goal of this lecture is to provide an introduction to the course by considering a problem that the students are unfamiliar with, developing an algorithm for the problem, and analysing the algorithm. The lecture took two full class sessions. The first lecture introduced the basic algorithm and showed that the algorithm was correct. The second lecture explored some advanced topics related to the algorithm. The first lecture is by far the most important of the two. I would like every student to have an understanding of the problem and algorithm. The second lecture is more of an enrichment topic. The material in the second lecture was to suggest what types of advanced topics can build on the basic understanding.

Slides where interaction with the students was anticipated were marked with Olympic mascots.

Course introduction

Slides 1 through 6. 00:00 through 08:33
Administrative material primarily for the University of Washington students. This material may be skipped (although you may wish to show Slide 6 which has the photos from Beihang).

Course philosophy

Slides 8-9, 08:33-15:27
This is an attempt to explain the philosophy of the course and the Kleinberg/Tardos text book. The two points are that algorithms are central to computer science and that the course is trying to teach "algorithmic thinking". A possible discussion topic is: what does the instructor mean by "algorithmic thinking?"

Definition of stable matching problem

Slides 10-11, 15:27-26:40
These two slides define the stable matching problem and the the formal definitions. It is very important that the concepts on these two slides be understood.

The notion of 'instability' is introduced by example at about 18:00. It might be good to stop at 18:30 to make sure students understand what the example means.

The key concepts are given on slide 11: Perfect Matching, Preference Lists, and Stability. These concepts should be made clear by the end of the slide.

There is a fairly good classroom discussion around slide 11 - this is a place where you might want to have a discussion as well. The student questions are quite clear, so you will be able to talk about them as well.

A few minor notes:

16:30

The discussion is about assigning 'Medical Residents' to hospitals. 'Residents' are doctors in training.

17:13

This is slightly confusing, since I say 'Teaching Assignments' instead of 'Teaching Assistants'

22:20

Instructor asks the class, "Is it clear . . .". A student asks a question at about 22:50. This question is quite clear on the tape. ("Is it an instability if only one of the nodes prefers the other"). Maybe the lecture should be stopped before the instructor answers this.

23:30

The student question was not entirely clear to me - so I was responding to what I thought the student asked.

24:00

This was another student question, which was a good question. It may be worth stopping to see if people understand the question and can answer it.

Stable Matching Examples

The next three slides are simple examples of stable matchings - they show the basic cases for two by two matchings. In class these examples were handled by asking students for verbal responses. My recommendation is the first example be handled verbally, by stopping the lecture (at about 27:40), and then do the second example as a student submission (note the mascot!) (at about 28:45). Discussion about the slides give several opportunities for stopping the video for discussion.

Proposal Algorithm

31:36 - 40:35, Slides 15-17
The next group of three slides introduce the proposal algorithm. The approach is to first give the key intuition for the algorithm, then put up some pseudo code for reference, and then work through a small example. The thought was that the small example (slide 17) would be done as a student submission at Beihang.

The discussion of the proposal operation takes about four minutes - this can be shown without stopping (unless there are questions). A question is asked at 35:35 - is the proposal algorithm better for M's or for W's. The student answer is recorded on the slide - but the instructor does not resolve the issue. (This is one of the important themes in lecture 2.) The example on slide 17 is stepped through with the assistance of the class - some of the student side comments may be hard to hear.

Performance Analysis

40:35-50:30, Slides 18-22
The final four slides give the correctness proof for the algorithm. This is a very nice proof which breaks down into steps. In general, I don't expect that the majority of students will follow the details of a proof during class. (My hope is that they will be able to understand the proof later when the look at the text, and recall the lecture). This, however is an exception. I want the students to follow the details of this proof: the individual steps are quite small and natural.

Slide 18: This slide gives three simple properties of the algorithm. These should be clear to the students, if there is confusion, stop for discussion.
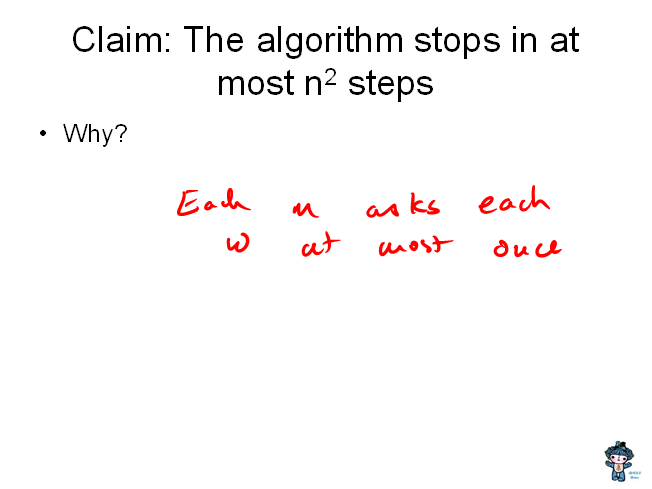
Slide 19: The first major step in the proof is to bound the number of steps - this follows directly from the maximum number of proposals that the M's could make. I asked the class at UW for the answer - but this could be done as a student submission, so that everyone thinks about it.
Slide 20: The second step is to argue that when the algorithm stops, all vertices are matched. One way of stating the answer is: If there is an unmatched w, there is also an unmatched m (since there is the same number of m's and w's). In that case, we know that m could not have proposed to w (otherwise w would be matched). This slide could be used as a student submission - but it may be better just to see if there are any verbal responses, and then show the UW discussion
Slide 21: The final step for the proof was covered a little bit quickly, since the class is coming to the end. This final detail is very important (since it is arguing that the result is correct) - so it would be appropriate to see if students have questions about this slide.