1 Intro
In class on Friday, we’ll discuss a concept called Huffmann codes, along with some more greedy algorithms that take a bit of ingenuity to figure out.
In some offerings of CSE 123, you implemented Huffman codes as a project. In this reading, you will either recap the setup of that problem, or become familiar with it for the first time.
2 Problem setup
At a high level, the goal is to represent text using binary, so that a computer can store and transmit it. We would like for this encoding to be as short as possible.
A computer’s default encoding of a text file often uses 8 bits
per letter, in a format called ASCII encoding. For example, a
capital A is encoded as the number 65 in binary, 01000001. We call
01000001 the codeword of A
. A mapping from symbols
to codewords is called a code.
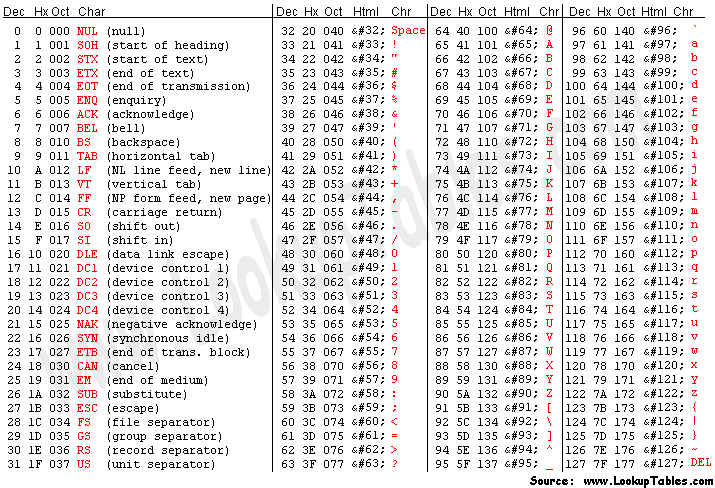
ASCII is a good system optimized for computer memory that stores 8 bits in 1 byte, but is not the most theoretically efficient way to store English text. If you only cared about the uppercase letters and some basic punctuation and spaces, you can definitely get away with only 32 symbols, which would take only 5 bits per symbol, not 8. Can we do even better?
3 Prefix codes
One interesting idea is to drop the requirement that all
codewords be the same length. Since some letters in the English
language appear more often than others, it might be a good idea to
make the codewords shorter for the most frequent symbols. (The
letters e
and t
appear about 100 times more often
than q
and z
!)
However, doing this naively would cause a decoding problem. Say
you had 6 symbols in a small language, with A
and B
occuring more often than C
, D
, E
, and
F
, and you gave the following encoding:
| Symbol | Codeword |
|---|---|
| A | 0 |
| B | 1 |
| C | 00 |
| D | 01 |
| E | 10 |
| F | 11 |
Although every symbol has a unique codeword, it’s unfortuantely
impossible to decode a string like 000
. Does this mean AAA?
Or AC? Or CA?
We fix this problem by requring our codes to be prefix codes. Prefix codes can be decoded uniquely back into the original text.
Definition. A code is called a prefix code if no codewords are prefixes of other codewords.
An example of a prefix code is:
| Symbol | Codeword |
|---|---|
| A | 00 |
| B | 01 |
| C | 100 |
| D | 101 |
| E | 110 |
| F | 111 |
Now, when you get a string like 00101110, you know that 00 must be A, because no other string starts with 00. Then 101 must be D, because no other string starts with 101. And 110 must be E. Thus, this decodes uniquely to ADE.
4 Comparing prefix codes
Given a piece of text and two prefix codes, how do we compare which prefix code is better? This is easy: encode the text using both codes, and the shorter one is better!
However, we would like a faster way to do this without having to encode the whole text. Instead, divide the encoded length by the original text length to get the average number of bits per symbol. We can compute this without encoding the whole text! If there are n symbols, and symbol i has frequency f_i and uses c_i bits in the code, the average number of bits per symbol is simply
f_1c_1 + \dots + f_n c_n
For example, say that A and B each appear 25% of the time, and C, D, E, and F each appear 12.5% of the time. Using the prefix code in the example above, the average number of bits per symbol will be:
0.25(2 + 2) + 0.125(3 + 3 + 3 + 3) = 2.5
Suppose instead, you did a suboptimal thing and for the same frequency list, used the following prefix code, giving short codes to infrequent symbols.
| Symbol | Codeword |
|---|---|
| A | 100 |
| B | 101 |
| C | 00 |
| D | 01 |
| E | 110 |
| F | 111 |
Then the average number of bits per symbol would be:
0.25(3 + 3) + 0.125(2 + 2 + 3 + 3) = 2.75
This is worse than the first prefix code that achieved 2.5, but still better than using a fixed-length code like ASCII. (A code that uses the same number of bits for every symbol would need at least 3 bits per symbol given 6 symbols.)
5 Looking ahead
We will explore an algorithm that can compute the mathematically optimal prefix code in lecture on Friday, called the Huffman code!