As we’ve discussed divide and conquer algorithms we’ve relied upon one key insight - that the smaller problems we divide into must be smaller versions of the exact same problem we’re trying to solve. We needed this because we wanted to rely upon recursion to solve those subproblems. In our next lecture we will investigate a small twist on this idea. We will still use recursion to write our algorithm, but this time we will see examples where we can write a more efficient algorithm by slightly modifying our goals so that we’re actually computing more.

To summarize the lesson we’ll see, we’re going to show examples where a divide and conquer algorithm can be made if we redefine it to compute more.

This may seem surprising or counterintuitive, but I like to think of the insight we’re leveraging like this. As we’re going through the recursion, the smaller subproblems may have opportunity to take notes that will help in the larger superproblem’s divide step. If the subproblem sends along those notes, then that could save the superproblem from needed to recompute those from scratch on the larger input.

In this reading we will look at a divide and conquer algorithm that follows the same pattern that we’ve already seen. In lecture we will show how computing more actually saves time.

1 Maximum Sum Subarray

Let’s jump into our example algorithm. Our algorithm’s goal is to solve a problem called Maximum Sum Subarray. Our task will be to take in an array of integers (positive and negative) and find a pair of indices i and j such that the subarray formed by taking indices i through j (inclusive) is maximum such subarray as well as the sum itself, then return i, j, and the value of the sum. To simplify this description a bit, we want to identify the contiguous region of a given array with the largest sum, then return the start point of that region, the end point of that region, and the sum of the values in between.

For example, if the array is [3, -5, 1, 3, -2, 3, 4, -8, 6 ] then the maximum sum subarray would be [ 1, 3, -2, 3, 4] with the sum 1+3-2+3+4=9, and so the algorithm will return the indices 2, 6, 9.

1.1 A Naive Algorithm

I general like first coming up with a naive or brute force algorithm for any new problem I see. For maximum sum subarray, the output is going to be a pair of indices of my given array. We could easily solve this problem by just computing the sum of all pairs of indices in the array, then returning whichever was largest.

Specifically we could so something like:

besti = -1
bestj = -1
bestSum = -infinity
for(int i = 0; i < arr.length; i++){ // select a starting index
    for(int j = i; j < arr.length; j++){ // select an ending index
        currSum = 0
         for(int k = i; k <= j; k++){ // sum the values in between
            currSum += arr[k];
        }
        if(currSum > bestSum){ // if this is the new best, update variables
            besti = i
            bestj = j
            bestSum = currSum
        }
    }
}
return besti, bestj, bestSum

(Brief aside, Java does not naturally allow for multiple values to be returned, but some other programming languages do. In Java we would need to either use an array or create some sort of custom object to contain the values of besti, bestj, and bestSum to return all of them.)

Now that we have an algorithm, let’s look at its running time to see what we need to beat! There are O(n^2) pairs of i and j that the algorithm must consider. For each such pair we need to sum the values in between, which takes linear time for the size of the range. In total, this algorithm’s running time will therefore be O(n^3).

1.2 Less Naive Divide and Conquer

Now let’s use divide and conquer to improve on this. We will actually write two divide and conquer algorithms here. The first will be a more straightforward divide and conquer algorithm following the same pattern we have seen thus far. After this we will look an updated one that employs the technique of computing more.

To write our divide and conquer algorithm, we need to define our three components: Base Case, Divide, and Combine.

For our base case, we can just say that if i=j then we just return i and j as the best range.

For divide, it’s pretty much always a good decision to just try breaking things in half first, so we’ll do that. For our divide step we split a given range i, j into two ranges i, (i+j)/2 and (i+j)/2+1, j.

The conquer step will then return the maximum sum subarrays for each of the left half and right half. I’ll call these iLeft, jLeft, iRight, jRight.

For our combine step, our task is to use iLeft, jLeft, iRight, jRight to find the maximum sum subarray for the whole array. To do this, we will recognize that the correct answer must be one of the following:

1. The left solution itself: in one case, the answer could just be the answer from the left subproblem, meaning the entire subarray is in the left half.
2. The right solution itself: similarly, the maximum sum region could be entirely in the right half of the array.
3. Something that spans the divide: If the correct answer is neither entirely within the left half, nor entirely within the right half, it must be that there is at least one value used in both halves.

With this observation, our conquer step will perform by finding the best answer than spans the divide, then returning the best of the left solution, the right solution, and this middle solution. All we need to do now, then, is identify a way to find the middle solution.

1.2.1 Finding the middle solution

Because this middle solution must include at least one element from each of the left half and the right half, we know that it specifically must use the last index from the left (all this lastLeft) and the first index from the right (call this firstRight). With this insight, we can determine the largest sum subarray that includes both of those elements by 1) finding the largest sum starting from anywhere on the left and ending at lastLeft (i.e. find the max sum suffix of the left half), 2) finding the largest sum start from firstRight and ending anywhere in the right (i.e. find the max sum prefix of the right half), 3) concatenating those together.

If we wish to find the middle solution for the region between indices start and end, we might then do the following:

findMiddleSolution(arr, start, end){
    // finding the best suffix of the left
    bestSuffix = (start+end)/2 // at first, the best suffix seen is only the last element on the left
    bestSuffixSum = arr[bestSuffix]  // so the sum is the value of that element
    currSum = bestSuffixSum
    for(int midStart = bestSuffix-1; midStart >= start; midStart--){ // from the middle going backwards
        currSum += arr[midStart] // add in the preceding element
        if(currSum > bestSuffixSum){  // check if starting the suffix one element sooner gives a larger sum
            bestSuffixSum = currSum // if so update the sum
            bestSuffix = midStart // and update the starting index
        }
    }
    // finding the best prefix of the right
    bestPrefix = (start+end)/2+1 // at first, the best prefix seen is only the first element on the right
    bestPrefixSum = arr[bestPrefix]  // so the sum is the value of that element
    currSum = bestPrefixSum
    for(int midEnd = bestPrefix+1; midStart <= end; midEnd++){ // from the middle going forwards
        currSum += arr[midEnd] // add in the next element
        if(currSum > bestPrefixSum){  // check if ending the prefix one element later gives a larger sum
            bestPrefixSum = currSum // if so update the sum
            bestPrefix = midEnd // and update the ending index
        }
    }
    // the best middle solution is the best suffix on the left followed by the best prefix on the right
    // The sum of the elements in this range is the sum of the elements in the prefix plus those in the suffix
    middleSum = bestSuffixSum + bestPrefixSum
    return bestSuffix, bestPrefix, middleSum
}

To summarize the behavior, this algorithm:

1. Starting from the end of the left half of the array, adds one element at a time, remembering which starting index gave the largest sum.
2. Starting from the beginning of the right half of the array, adds one element at a time, remembering which ending index gave the largest sum
3. Returned the subarray including the entire region consisting of the left-side suffix and the right-side prefix.

1.3 Our divide and conquer algorithm

We have now identified all of the pieces of our divide and conquer algorithm, so let’s take a moment to summarize the whole thing and then find its running time.

For finding the maximum sum subarray of array arr starting from index start and ending at index end

Base Case: If there is only one element in our current subproblem, return that element’s index as the start and end, and return that element’s value as the sum

Divide: Split our current subproblem in half by index. This creates subproblems from start to (start+end)/2 and from (start+end)/2 to end.

Conquer: recursively solve both subproblems. We will say that the maximum sum on the left is leftSum, the maximum sum on the right is rightSum, the left solution goes from index leftStart to index leftEnd, and the right solution goes from index rightStart to rightEnd.

Combine: find bestSuffix, bestPrefix, middleSum according to the procedure above. Then compare leftSum, rightSum and bestPrefixSum+bestSuffixSum. If leftSum is largest then return leftStart, leftEnd, and leftSum. If rightSum is largest then return rightStart, rightEnd, and rightSum. If middleSum is largest then return bestSuffix, bestPrefix and middleSum.

1.3.1 Running time

Let n represent the number of elements from index start to end. Our divide step splits our problem into 2 subproblems, each of size n/2 and requires O(1) work to do. Our combine step requires O(n) work. This gives us the recurrence relation T(n)=2T(\frac{n}{2}+n. You may recognize this as the same recurrence we saw for Mergesort! We already know that the master theorem gives us a running time of O(n log n).

In class, we will describe a procedure that computes and returns more items per stack from to result in a O(n) algorithm.

1.3.2 Example execution

To make sure we understand, here’s an example execution of our algorithm using the array arr = [3, -5, 1, 3, -2, 3, 4, -8, 6 ], expecting the answer 2, 6, 9. (indicating the maximum sum spans from index 2 to index 6 and has sum 9.

We will only look 1 deep into the recursion to see where the answers come from.

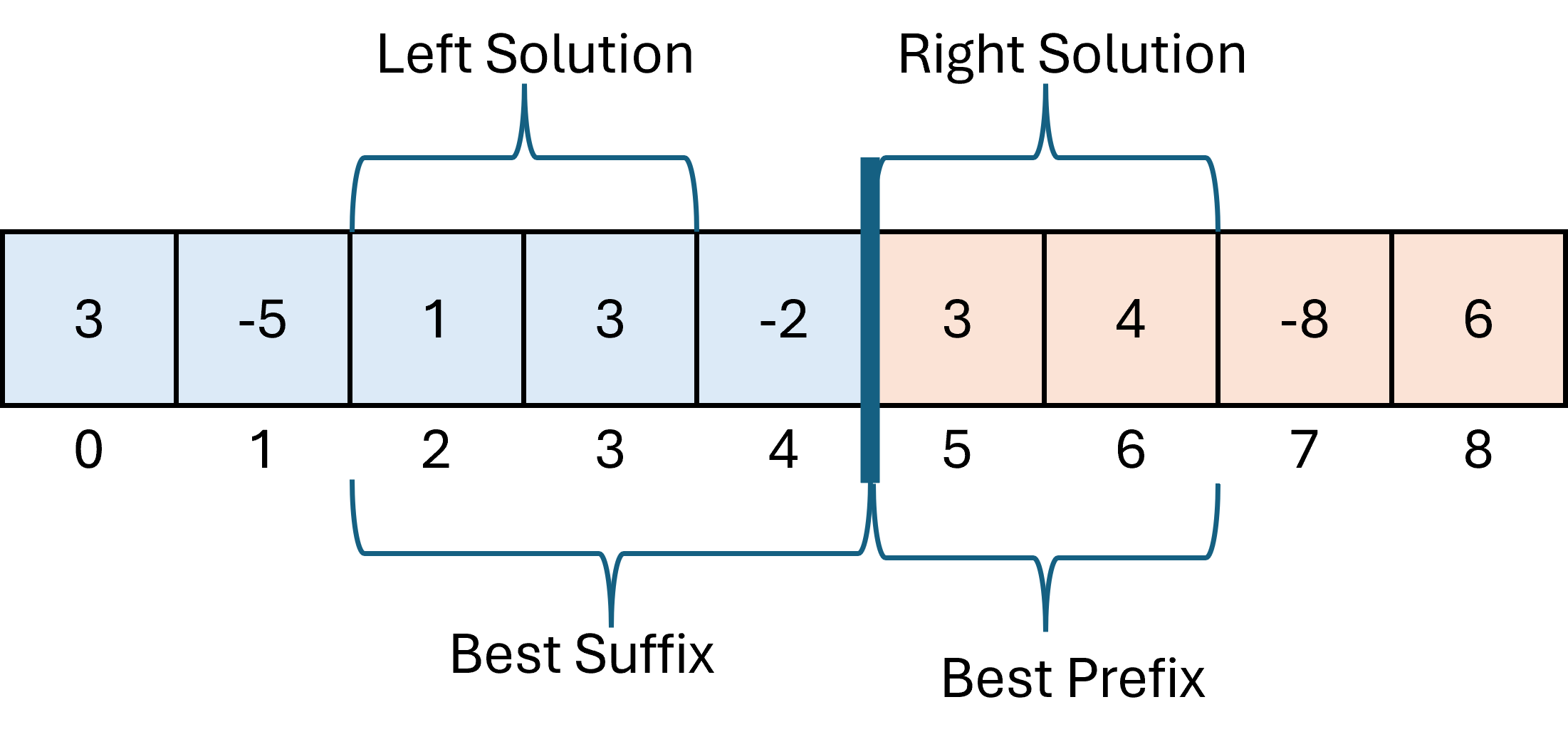
=====stack frame for 0,8=====

To begin, we have start = 0 and end = 7. We are not in a base case, so we divide into two subproblems, one for indices 0 to 4, the other from 5 to 8.

From the subproblem for 0,4 we will have leftStart = 2, leftEnd = 3, and leftSum = 4. From the subproblem for 5,8 we have rightStart = 5, rightEnd = 6, and rightSum = 7.

From here we want to find the middle solution, so we want the max sum subarray from the range 0 to 8 which includes indices 4 and 5 (so values -2 and 3). The best suffix on the left is the range 2,4 which has a sum of 1+3-2=2. The best prefix on the right is the range 5,6 which has sum 3+4=7. This means that the middle solution is the range 2,6 which has sum 9.

Finally we return the best of the three solutions. Since leftSum is 4, rightSum is 8, and midSum is 9, the best answer is the middle solution, so we return 2, 6, 9.

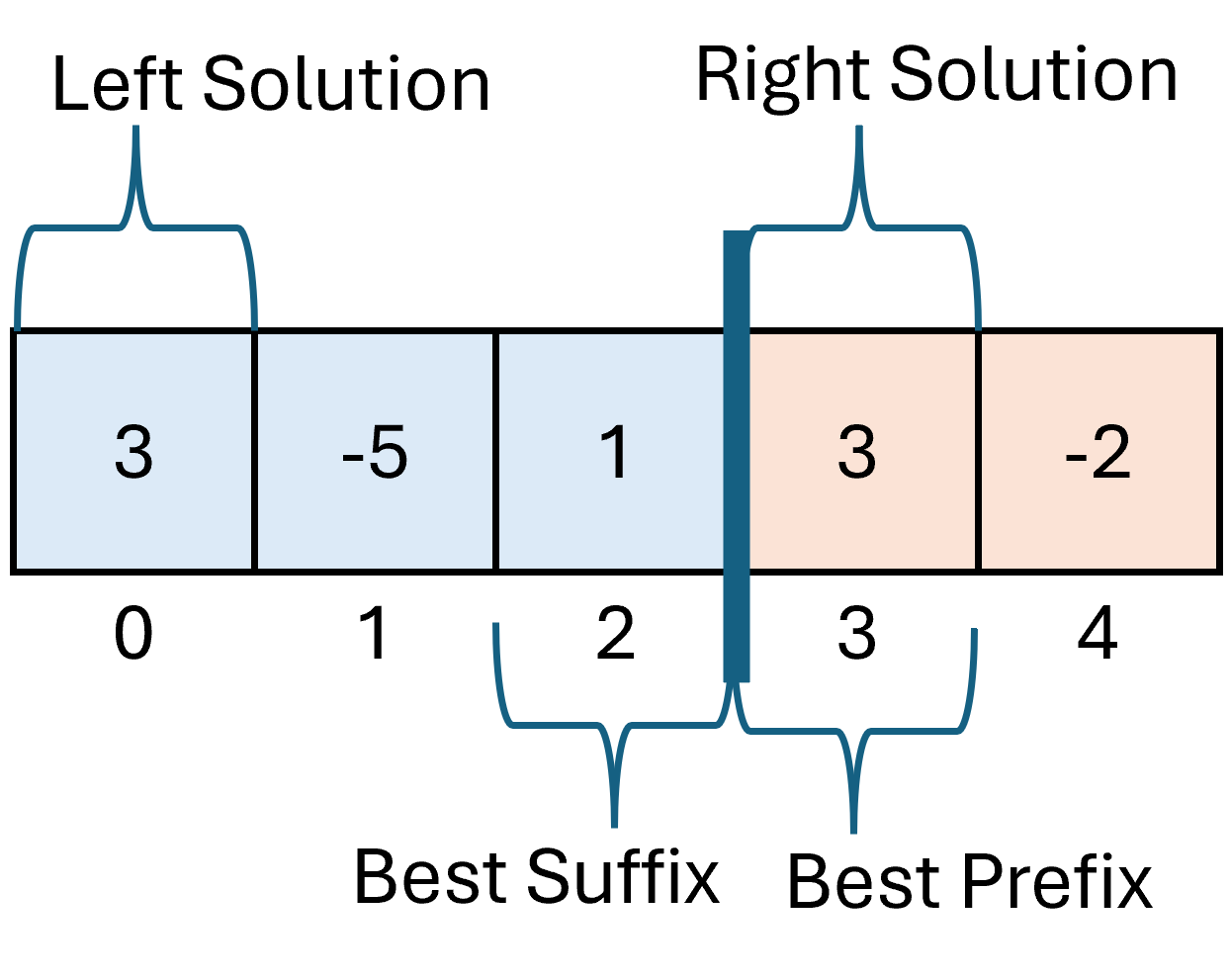
=====stack frame for 0,4=====

In this stack frame we’re working with the subarray arr = [ 3, -5, 1, 3, -2]. We are not in a base case, so we divide into two subproblems, one for indices 0 to 2, the other from 3 to 4.

From the subproblem for 0,2 we will have leftStart = 0, leftEnd = 0, and leftSum = 3. From the subproblem for 3,4 we have rightStart = 3, rightEnd = 3, and rightSum = 3.

From here we want to find the middle solution, so we want the max sum subarray from the range 0 to 4 which includes indices 2 and 3 (so values 1 and 3). The best suffix on the left is the range 2,2 which has a sum of 1. The best prefix on the right is the range 3,3 which has sum 3. This means that the middle solution is the range 2,3 which has sum 4.

Finally we return the best of the three solutions. Since leftSum is 3, rightSum is 3, and midSum is 4, the best answer is the middles solution, so we return 2, 3, 4.

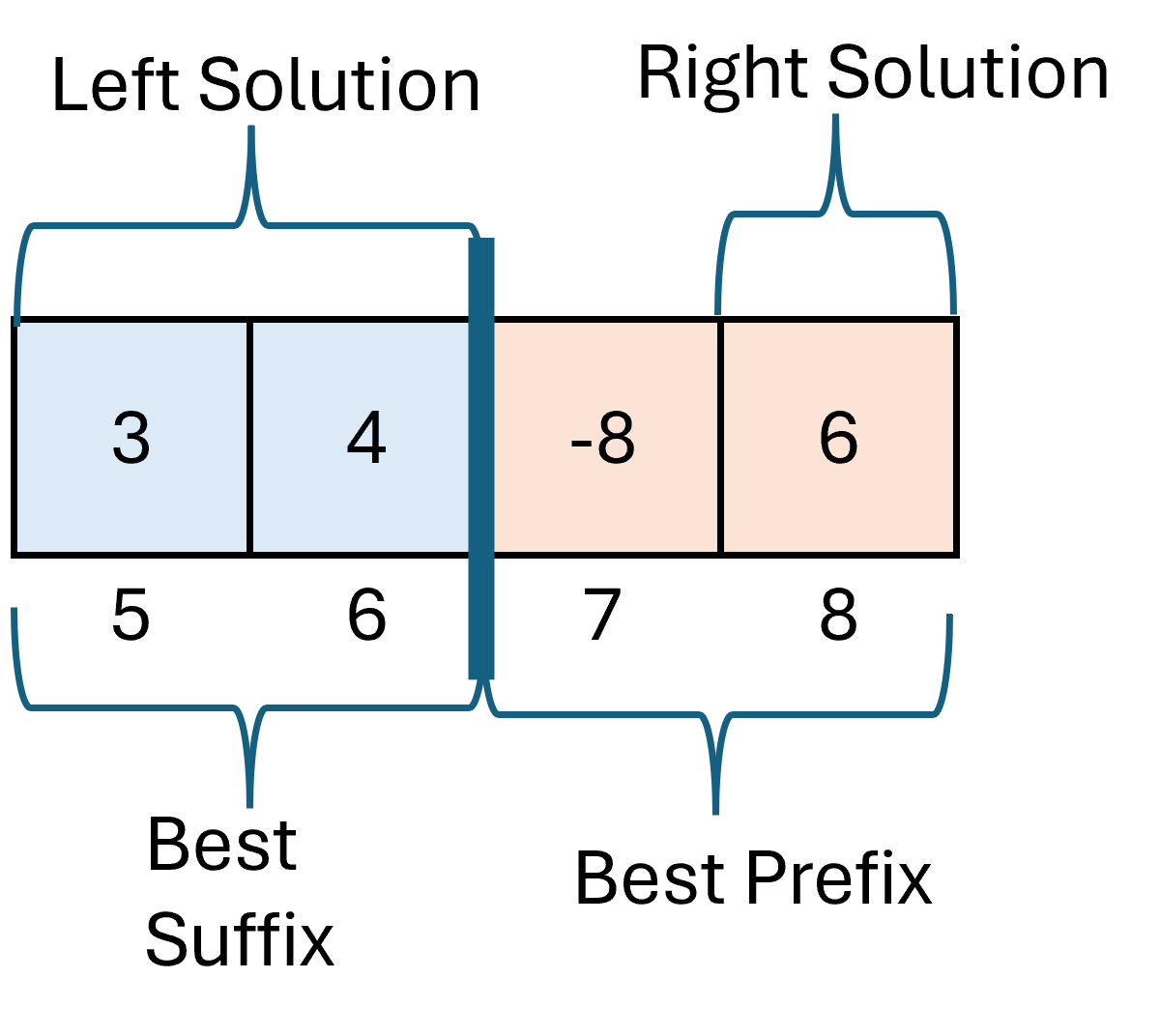
=====stack frame for 5,8=====

In this stack frame we’re working with the subarray arr = [ 3, 4, -8, 6]. We are not in a base case, so we divide into two subproblems, one for indices 5 to 6, the other from 7 to 8.

From the subproblem for 5,6 we will have leftStart = 5, leftEnd = 6, and leftSum = 7. From the subproblem for 3,4 we have rightStart = 8, rightEnd = 8, and rightSum = 6.

From here we want to find the middle solution, so we want the max sum subarray from the range 5 to 8 which includes indices 6 and 7 (so values 4 and -8). The best suffix on the left is the range 5,6 which has a sum of 7. The best prefix on the right is the range 7,8 which has sum -2. This means that the middle solution is the range 5,8 which has sum 5.

Finally we return the best of the three solutions. Since leftSum is 7, rightSum is 6, and midSum is 5, the best answer is the left solution, so we return 5, 6, 7.