This assignment covers state-space search in single-agent, deterministic environments. Later we will consider multi-agent search in environments with stochastic dynamics. We start by introducing a framework for the classical theory of problem solving. Then we examine heuristic search. Note that this assignment has two parts. Part 1 is an "individual work" sub-assignment, and must not be done in partnerships or groups. (When the graders find evidence of academic misconduct such as plagiarism, these cases are reported to the administration. Please do not copy, collaborate, or otherwise allow this to happen.) Part 2 is a "collaborative work" sub-assignment, in which you are encouraged to work with a single partner, i.e., in a team of two people. If you have a strong desire to be in a group of three, please email the lead TA (Teerapat) with a request and a good reason for the request, giving the names of all three proposed team members.

Along with various Python files, you'll be submitting two separate report files, one called BlindSearches.pdf (that you create in Part 1) and one called HeuristicSearches.pdf (that you create in Part 2).

Each student should do Part 1 without collaboration. This part is about basic problem formulation and basic search algorithms.

Although both Part 1 and Part 2 are due on Monday, October 16, there is an option to submit your solution for Part 1 early and receive a 5-point bonus. To get the bonus, you must do two things: submit your Part 1 files by 11:59 PM on Wednesday, October 11, to GradeScope, and you must submit the name of your partner for Part 2. If you do submit early, you retain the right to resubmit Part 1 later, but the bonus will not accrue in that case. Also, to get the bonus in Part 1, you have to have a partner in Part 2, name the partner in your early-bird submission, and follow through with the partner in Part 2.

1. First, download the starter code for this assignment. Unzip it with a utility such as Windows Compressed Folders, etc.

In the given formulation files, pay particular attention to how the State class is defined and how the operators are established. We will be talking about this code in class.

python3 Int_Solv_Client.py TowersOfHanoi 3

7. The starter-code file UCS.py, provides an implemention of the Uniform-Cost Search algorithm. This file also provides you with an implementation of a special kind of priority queue which supports not only the standard insert and delete_min operations, but also a method called contains, which returns True if a given element is in the priority queue. It also allows accessing and updating the priority value of any element in the priority queue. See the documentation for more information. This priority queue is not just adequate for implementing Uniform-Cost Search, but is particularly helpful in implementing the A* Search algorithm.
The main difference between Breadth-First Search and Uniform-Cost Search (UCS) is that UCS works with problem formulations that have different costs associated with different moves. In terms of graph search, there are edge costs, and they are not necessarily assumed to be all equal to 1 as they essentially are in Breadth-First Search.

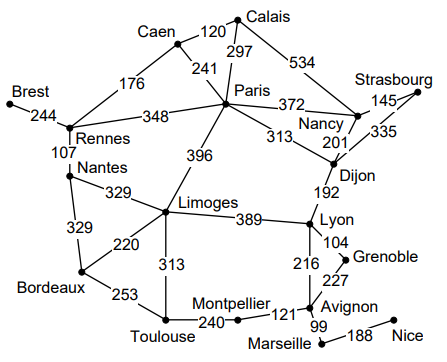
The starter code includes a new problem formulation for you to use with UCS; it's the French Cities network in which the problem is to find a shortest route from the initial-state city to the goal-state city. These are, by default, RENNES and AVIGNON. (These could easily be changed by editing the formulation file's line defining STARTING_CITY, etc.) This formulation is in the file FranceWithCosts.py.
The State class in this formulation file has a method edge_distance(s2), which is used to get the edge cost from the current state to s2. You'll be setting up the UCS.py program to use these cost values to determine the cost of the lowest-cost path from the starting state to any newly reached state.
When the UCS algorithm reaches a goal state, it produces a backtrace of "backlinks" (sometimes called predecessor links) to represent the actual lowest-cost path from the start state to the goal state found. The file UCS.py includes a method runUCS.

For the default initial state and goal state, the results are

['Rennes', 'Nantes', 'Limoges', 'Lyon', 'Avignon']

1041.0

Page 184 in the reading shows the state space for this problem, with the distances on the graph edges. When you run the code you should get a solution path of 4 edges (5 cities) and total distance 1041: [’Rennes’, ’Nantes’, ’Limoges’, ’Lyon’, ’Avignon’]. It might be formatted differently in the printout. The map is also shown below:

Map showing French cities (which serve as the states of this problem) and distance values on roads (represented as graph edges) between them.

Implement an A* search program, putting your code into the starting template file AStar.py. You may wish to cut and paste from the UCS.py file, since most of the implementation will be identical.

Develop your A* program to work with the heuristic function defined in the file FranceWithDXHeuristic.py. Your program will be operated as follows:

python3 AStar.py FranceWithDXHeuristic

Here are some hints about how to modify UCS.py to implement A*. Change the names of the file and the algorithm in the code and the comments. After the code that imports the Problem, assign self.h = Problem.h, so that you can call the heuristic function easily in your algorithm. Within the search algorithm, any time UCS uses gs or new_g as a priority value, you should compute f (or call it fs or new_f, depending on the context), and use the f value as the priority.

When checking the CLOSED list, don't necessarily delete the new state if the same city is already on CLOSED, but look at the priority, and if the new state has a lowever priority value, delete the state on CLOSED and put the new one on OPEN.

Make sure that the first five CAPITALIZED variables in class AStar get assigned the values they need (as described in the corresponding comments), so that you can receive credit on autograder tests. These include self.COUNT through self.TOTAL_COST. The solution path should be set as the value of self.PATH, and it must be a list of strings, such as ['Rennes', 'Nantes', 'Limoges', 'Lyon', 'Avignon']. Also, be sure to assign proper values in the dictionary for self.g.

Try to solve some instances of the Eight Puzzle using UCS.py. There is a default instance you should try first. You can do it with the command line:

python3 UCS.py EightPuzzle

python3 UCS.py EightPuzzle '[[3, 1, 2], [4, 5, 0], [6, 7, 8]]'

python3 UCS.py puzzle_rotate_2

Example puzzles to try:

# Puzzle A. (should be very fast)
python3 UCS.py EightPuzzle '[[3,0,1],[6,4,2],[7,8,5]]'

# Puzzle B. (should not take long)
python3 UCS.py EightPuzzle '[[3,1,2],[6,8,7],[5,4,0]]'

# Puzzle C. (May take a few minutes)
python3 UCS.py EightPuzzle '[[4,5,0],[1,2,8],[3,7,6]]'

# Puzzle D. (May take several minutes)
python3 UCS.py EightPuzzle '[[0,8,2],[1,7,4],[3,6,5]]'

# Test with Puzzle A:
python3 AStar.py EightPuzzleWithHamming '[[3,0,1],[6,4,2],[7,8,5]]'

You'll be turning in a report for this part of the assignment in addition to your code (see below). Create a section of your report called "Heuristics for the Eight Puzzle". Compare the performance of these heuristics on each of the example puzzles (given above). For each puzzle-heuristic pair, report (a) whether the puzzle was successfully solved, (b) length of the solution path found, in number of edges, (c) total cost of the path found, (d) number of states expanded, and (d) MAX_OPEN_LENGTH. Put this information into the table, described below.

The table should have a row for each puzzle instance and heuristic (e.g., "(Puzzle A, Hamming)", and columns for the following: puzzle instance permutation (e.g., [3,0,1,6,4,2,7,8,5]; this flattened list is OK here), success (yes/no), count of expanded nodes, aborted (yes/no). If it takes more than 5 minutes to solve a particular problem with a particular heuristic then note that; you may abort such runs. You are welcome to use the format for your report: shown in the starter-code file named HeuristicSearches-template.txt.

Here are some ideas to keep in mind for this assignment. The problem format we are using not only permits the "manual solving" that you do with the Interactive Solving Client. It also permits automatic solving, such as with DFS, and BFS. Thus it is important that you follow the problem structure correctly. Certain methods are required in the State class, including __init__, __eq__, __hash__, __str__, and copy. The operators must have the correct structure, as well. The nice thing about the Interactive Solving Client is that it provides a pretty good means to test whether your formulation will be OK.

Even if you are familiar with Python, there may be some constructs in the formulation files that you are not familiar with. You can read up on list comprehensions (p.31 of the first reading) and lambda expressions (pp. 47-52 of that reading). We'll also cover them in class.

Parts of your code will be graded by an autograder. To do this, your files will be imported as modules by the autograder. Your search should not automatically start running when the module is imported. The starter template file AStar.py comes with some code at the end of the file that takes care of this. This code is: "if __name__ == '__main__' " which avoids running the search automatically if it is being imported, but still runs it automatically if it is the main program. The autograder will be comparing the solutions and statistics found by your code with expected solutions, by calling functions in your code and examining the values of certain variables in your code. These variables are generally already in place for you in the starter code UCS.py. So you should not rename variables like self.PATH or any of the other variables written with all CAPITAL letters.

Each of your Python files should begin with a multiline string (more details are shown below.)

Follow reasonable commenting practice in your code. The comments in the starter code can serve as examples of the commenting style that we consider appropriate.

For Part 1, turn in the following files to GradeScope:

partnership-plan.txt
Farmer_Fox.py
FFCG-log.txt
ItrBFS.py
BlindSearches.pdf
Here partnership-plan.txt will tell us whom you are working
with in Part 2.  Each partner in a planned team needs to provide this information
along with an early submission of Part 1 files in order to qualify for an early-bird bonus.

For Part 2, turn in the following files to GradeScope:
partnership-retrospective.txt
AStar.py
EightPuzzleWithHamming.py
EightPuzzleWithManhattan.py
HeuristicSearches.pdf

Here partnership-retrospective.txt will contain (a) the names of
the people in your team, and (b) how you divided up the work in Part 2.

Each of the Python files should start with a multiline comment in the following format
with your own information rather than the sample information given here.
'''Farmer_Fox.py
by John Nathan Smith
UWNetID: jnsmith98
Student number: 9876543

Assignment 2, Part 1, in CSE 415, Autumn 2023.
 
This file contains my problem formulation for the problem of
the Farmer, Fox, Chicken, and Grain.
'''



The turn-in method is via file uploads to GradeScope. Be sure to upload your Part 1 files
to the A2-Part-1 assignment, and upload your Part 2 files to the A2-Part-2 assignment.
We expect to grade this assignment semi-automatically, and having files in the wrong places
might lead to unnecessary losses in points.

If needed, updates and corrections will be posted here, and/or in ED.