| PART I: Creating a Game-Playing Agent (80 points).
Create a program implementing an agent that can participate in a game of Toro-Tile Straight (defined below).
Your program should consist of a single file, with a name of the
form [UWNetID]_TTS_agent.py, where [UWNetID] is your own UWNetID.
For example, my file would have tanimoto_TTS_agent.py for its name.
Although you create one Python file for this assignment, it will contain a
collection of specific functions for playing games of "Toro-Tile Straight".
We define a Toro-Tile Straight game as a kind of generalized
K-in-a-Row with the following features:
-
(a) Just as in a game like Othello,
there are two players: one plays White and the other plays Black;
-
(b) the
board is rectangular, but is not necessarily 3 by 3; it is mRows by
nColumns, where these dimensions are chosen by the Game Master (referee) at the
beginning of the game;
-
(c) a player wins by getting K in a row, where
K is not necessarily 3; K can be any integer greater than 1;
-
(d) the topology of the board is toroidal. This means that the
left edge and right edge of the board can be considered equivalent,
and the top and bottom edges can be considered equivalent.
If a piece is placed in the left column of the array, then
moving one unit in the West direction is defined to "wrap around"
to the rightmost column (but same row).
Similarly, moving South from the bottom row, wraps around to the
top of the same column.
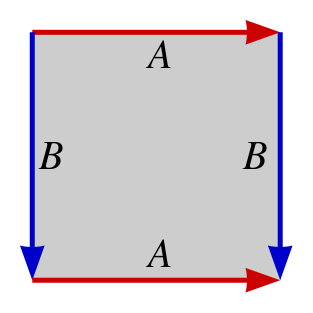
The toroidal topology is illustrated above, with line segments A unified,
as well as line segments B unified. These are at the outer boundaries of the
array.
In a discrete space, lines of tiles just "wrap around" when they go off
the edges of the board. Here is an illustration of the ways to get 3 in
a row on a 3 by 3 board. Note that the first 8 are the familiar Tic-Tac-Toe
wins, but that there are four more, due to the toroidal topology.
W W W - - - - - -
- - - W W W - - -
- - - - - - W W W
W - - - W - - - W
W - - - W - - - W
W - - - W - - - W
W - - - - W
- W - - W -
- - W W - -
- W - - W - W - - - - W
W - - - - W - - W W - -
- - W W - - - W - - W -
-
(e) there can be
"forbidden squares" on the board; these are chosen at the beginning
of the game by the Game Master; a square on the board that is available
is represented by a blank, whereas a forbidden square is
represented by a dash "-" ;
-
(f) there can be "handicaps" in the initial state, meaning that some
White and/or Black tiles can be set up on the board by the Game Master in order
either to influence the succeeding play or to change the balance of advantage and disadvantage
to the players.
You can see a full
transcript of a sample game here. The two agents that played this game
are very dumb, but they followed the rules. The code for each of these agents is part of
the starter code. You can use this code to organize the required functions, adding to
them to create a good player.
It will be essential that your program use the provided
representation of a game state, so that it is compatible with all the
other A5 TTS game agents developed in the class.
Your program should be designed to anticipate time limits on
moves. There are two aspects to this: (1) use iterative
deepening search, and (2) poll a clock frequently in order to
return a move before time runs out.
In addition to being able to play the game, your program should make an
utterance --- that is, a
comment in each move, as if participating in a dialog. Ideally, your
program would have a well-defined "personality". Some examples of
possible personalities are these: friendly; harmless joker; blunt
joker; paranoid; wisecracker; sage; geek; wimp; competitive freak;
fortune-teller (based on the state of the game). The personality will
be revealed during games via the "utterances" made by the
program. (For more details, see the description of the take_a_turn
function below.)
Your program must include the following functions. You can have helper
functions if you like. Please keep all the functions required by your
player in just one Python file that follows the naming convention
mentioned earlier. For example, my player would be in a file
tanimoto_TTS_agent.py. This will facilitate your player's being part of
the class tournament.
-
parameterized_minimax(current_state=None, max_ply=2, use_alpha_beta=False, use_basic_static_eval=True).
This method will let both you and the graders execute a search under a specific set of
conditions without having to set up a full TTS game. You can assume this function
will be called after get_ready(), though not during the course of a normal game.
This method accepts a set of parameters that determine
how the minimax search will run.
Here are what the various arguments mean:
- current_state=None: This field will be assigned a valid TTS state that
should be used as the root node for minimax search that will occur in this method
function call.
- max_ply=2: This field determines the maximim allowed depth of your minimax search.
This should limit the search regardless if iterative deepening is enabled or not.
- use_alpha_beta=False: This field determines if the search should use alpha-beta pruning or not.
- use_basic_static_eval_function=True: This field determines if you should
use the basic eval (described below) or your own custom eval function during the search.
You should use a "standard"
move generation method within
parameterized_minimax.
That method is to order available spots on the board from left-to-right,
top-to-bottom. That is, if your board is an empty 2x2 grid, the move generation method
should generate [upper-left, upper-right, lower-left, lower-right] in that order. This
is necessary for us to consistently test your pruning algorithm.
Within parameterized_minimax, do not use iterative deepening.
When this method ends its search it should return a dict of
attribute-value pairs giving ata related to how it executed the search.
- 'CURRENT_STATE_STATIC_VAL': The static eval value of the current_state as determined by your minimax search
- 'N_STATES_EXPANDED': The number of states expanded as part of your minimax search
- 'N_STATIC_EVALS': The number of static evals performed as part of your minimax search
- 'N_CUTOFFS': The number of cutoffs that occurred during the minimax search (0 if alpha-beta was not enabled)
It is important that
you implement this function in a manner consistent with the options you are
handling, particularly the more advanced features such as alpha-beta pruning.
Certain basic features of your code may also be tested using this function, and
so you'll want to handle this well, both for testing your own code as you go and
to allow any autograder system to award you as many points as possible.
-
get_ready(initial_state, k, what_side_i_play, opponent_moniker).
This function takes four arguments and it should
"remember" these values for the game that is about to be
played. (However, if your agent is in a match with itself
say for testing purposes, this
get_ready method will be called twice. In this case, be careful not to
let the agent assume it is playing 'B' on both turns.)
The first parameter, initial_state, allows your agent to figure out
any needed properties of the game board before the playing begins.
It is a legal game state that can be used by your player, for example,
to determine the dimensions of the board, the locations of forbidden
squares, and even the locations of any handicap items.
The second parameter, k, is the number of pieces in a row (or column
or diagonal) needed to win the game.
The parameter what_side_i_play is 'W' if your agent will play as White; it is
'B' if your agent will play Black.
The parameter opponent_moniker allows your utterance-generation mechanism to refer
to the opponent by name, from time to time, if desired.
Note that your program does not really have to do much at all when its
get_ready method is called. The main thing it should do is return
"OK". However, the get_ready function offers your agent an
opportunity to do any initialization of tables or other structures
without the "clock running."
This could be used to do any preprocessing related to, say, speeding up
move generation, e.g., finding out which
of the four directions a win can occur from a particular square -- a list of all the
squares on the board where such a winning line could actually start.
Having these lists can save time in your static evaluation function.
-
who_am_i().
This function will return a multiline string that introduces your
player, giving its full name (you get to make that up), the name and
UWNetID of its creator (you), and some words to describe its
character.
-
moniker().
This function should return a short version of the playing agent's
name (16 characters or fewer). This name will be used to identify the
player's moves in game transcripts.
-
take_turn(current_state, opponents_utterance, time_limit=3).
This is probably your most important function. Unlike the parameterized_minimax function described below,
this method should always use your most advanced search techniques (while still respecting
the time limit) to make your agent as competitive as possible. It should return a
list of the form [[move, new_state], new_utterance].
The move is a data
item describing the chosen move.
The new_state is the result of making the move from the given
current_state. It must be a complete state and not just a board.
The opponents_utterance argument is a string representing a remark from the
opponent on its last move.
The time_limit represents the number of seconds available for
computing and returning the move.
The new_utterance to be returned must be a string. During a game, the
strings from your agent and its opponent comprise a dialog. Your
agent must make "interesting" utterances, described in more detail in the feature section.
-
static_eval(state).
This function will perform a static evaluation of the given state.
The value returned should be a number that is high if the state is good for White and low
if the state is good for Black. See the MY_TTS_State class provided in the starter code
in PlayerSkeleton.py
for where to invoke the two required versions of this. Here is a description
of these two versions:
- basic_static_eval(self):
This is probably the very first function you should implement.
It must compute the following value accurately (whereas with your
custom function, you'll get to design the function to be computed).
Depending on the game type, there will be a particular value of K,
the number of tiles a player must place in a straight line in order
to win.
We define a "piece" on the board to be either a W tile or a B tile.
We define a "freedom" of a tile t on the board to be any unoccupied square
that is one of t's (up to eight) neighbors. A neighbor of t touches t either
along an edge or at a corner of the tile.
Each piece has some number of freedoms, in the range 0 to 8.
Let TWF be the total of the numbers of freedoms of all the W tiles on the
board, and let TBF be the total of the numbers of freedoms of all the B tiles.
Then our basic static value is just TWF - TBF. If White has more total freedoms
than Black does, then the value will be positive, etc.
An autograder will be checking to make sure your function comes up with the right
numbers for various given states.
- custom_static_eval(self):
You get to design this function. You'll want it to perform "better" than the
basic function above. Here better could mean any of the following:
(a) more accurate assessment of the value of the board, to better inform
the choice of the best move, (b) faster to compute, or (c) achieving a better
combination of accuracy and efficiency than the basic function.
(It might be less efficient, but a lot more accurate, for example.)
Two motivations for putting some thought into this function are: (i) your
agent's ability to play well depends on this function, and (ii) an autograder
will likely try comparing your function's values on various states, looking for
reasonable changes in value as a function of how good the states are, in terms
of likelihood of a win.
|
| PART II: Game Transcript (20 points).
Follow the directions below to produce a transcript of a match
between your agent and another student's agent.
Using the timed_tts_game_master.py program to run a Gold Rush match, create
a transcript of a game between your agent and the agent of another
student in the class.
Set up the match so that your agent plays White and your opponent plays
Black. Use the following game instance for your match.
For this run, you
should set a time limit of 1.00 seconds per move.
This can be specified on the command line when you run
timed_tts_game_master.py.
The following is the representation of the initial board in a TTS game we are calling
"Gold Rush" in which the objective is to get a (connected) line segment of five tiles.
The line may go horizontally, vertically, or diagonally.
[[['-',' ',' ','-',' ',' ','-'],
[' ',' ',' ',' ',' ',' ',' '],
[' ',' ',' ',' ',' ',' ',' '],
['-',' ',' ','-',' ',' ','-'],
[' ',' ',' ',' ',' ',' ',' '],
[' ',' ',' ',' ',' ',' ',' '],
['-',' ',' ','-',' ',' ','-']], "W"]
Note that in the following state, White has just won, because there is a
diagonal line of Ws that starts near the lower left corner of
the space, and continues up and to the right, wrapping around twice in
the toroidal space (once from right to left, and once from top to bottom).
With the upper-left square (which happens to be forbidden in this game) at row 0, column 0,
we can describe White's winning line as this sequence of locations:
[(3,5), (2,6), (1,0), (0, 1), (6, 2)]
[[['-','W',' ','-',' ',' ','-'],
['W',' ',' ',' ',' ',' ','B'],
[' ',' ',' ',' ','B','B','W'],
['-',' ',' ','-',' ','W','-'],
[' ',' ',' ',' ',' ',' ',' '],
[' ',' ','B',' ',' ' ' ',' '],
['-',' ','W','-',' ',' ','-']], "B"]
It is not required that the line of tiles involve the toroidal wraparound.
Five in a line somewhere near the middle of the board could also win, for example.
However, the wraparound feature can often help to open up many more possibilities for winning.
The timed_tts_game_master program will automatically generate an HTML file containing a formatted game
transcript of your game. Turn in that HTML file.
|
