| Assignment 6: Markov Decision Processes and Computing Utility Values |
|
CSE 415: Introduction to Artificial Intelligence The University of Washington, Seattle, Spring 2019 |
|
The search theme continues here, except that now our agents
operate in a world in which actions may have uncertain outcomes.
The interactions are modeled probabilistically using the
technique of Markov Decision Processes. Within this framework,
the assignment focuses on two approaches to having the agent
maximize its expected utility: (A) by a form of planning, in which
we assume that the parameters of the MDP (especially the transition model T and
the reward function R) are
known, which takes the form of Value Iteration, and
(B) by an important form of reinforcement learning, called
Q-learning, in which we assume that the agent does not know the
MDP parameters. Part A is required and worth 100 points, while Part B is for 10 points
of extra credit.
NOTE: This assignment requires the use of the IDLE integrated development environment, unless you wish to spend a substantial amount of extra time, on your own, configuring your PyCharm or other IDE to use Tkinter. Reports of people who have tried to use Tkinter with other IDEs suggest that a lot of time can be wasted figuring out workarounds for different operating systems, Python versions, and IDE versions. Our advice is, if you already use IDLE, stick with it for this assignment, and if you don't already use IDLE, try it out for this assignment. It's easier to learn than almost any other other Python IDE. IDLE ships with the standard Python distribution from Python.Org, so it is probably already installed on your system. If you don't like IDLE for editing, you could possibly edit the code in another tool, and then reload it into IDLE to run it, but that would feel inconvenient for most of us. The particular MDPs we are working with in this assignment are variations of a "TOH World", meaning Towers-of-Hanoi World. We can think of an agent as trying to solve a TOH puzzle instance by wandering around in the state space that corresponds to that puzzle instance. If it solves the puzzle, it will get a big reward. Otherwise, it might get nothing, or perhaps a negative reward for wasting time. In Part A, the agent is allowed to know the transition model and reward function. In Part B (optional), the agent is not given that information, but has to learn it by exploring and seeing what states it can get to and how good they seem to be based on what rewards it can get and where states seem to lead to. |
| Due Tuesday, May 21 via Canvas at 11:59 PM. |
| What to Do.
Download the
starter code.
Start up the IDLE integrated development environment that
ships with the standard distribution of Python from Python.org.
In IDLE, open the file
TOH_MDP.py. Then, using the Run menu on this file's window, try running the starter code by
selecting "Run module F5".
This will start up a graphical user interface,
assuming that you are running the standard distribution of Python 3.6 or Python 3.7,
which includes the Tkinter user-interface technology.
You can see that some menus are provided. Some of the menu choices
are handled by the starter code, such as setting some of the parameters
of the MDP. However, you will need to implement the code to actually
run the Value Iteration and, if you choose to do the optional Part B, the Q-Learning.
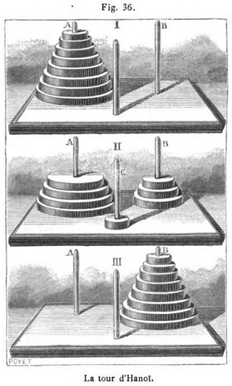 Figure 1. An early description of the problem "La Tour d'Hanoi" from the 1895 book by Edouard Lucas. Your program will determine an optimal policy for solving this puzzle, as well as compute utility values for each state of the puzzle. |
| PART A: Implement Value Iteration (100 points).
There is a starter file called YourUWNetID_VI.py. Rename the file according to this format and your own UWNetID. Also, change the name within TOH_MDP.py where this file is imported. Complete the implementation of the functions there:
|
| A Sample Test Case.
Once your implementation is complete, you should be able to duplicate the following
example display by setting the following parameters for your MDP and VI computation:
from the File menu: "Restart with 2 disks"; from the MDP Noise menu: "20%";
from the MDP Rewards menu: "One goal, R=100"; again from the MDP Rewards menu: Living R= +0.1;
from the Discount menu: "γ = 0.9"; from the Value Iteration menu:
"Show state values (V) from VI", and "100 Steps of VI" and finally "Show Policy from VI."
|
| Report for Part A.
Create a PDF document that includes the following questions (1a, 1b, etc.) but also their answers. The document should start with this: Assignment 6 Report for Part A (your name)Name the file using this naming pattern: YourUWNedID_A6_Report.pdf. The following tells you what to do and what questions to answer
|
| (OPTIONAL) PART B: Implement Q-Learning (10 points).
Start by renaming the skeleton file YourUWNetID_Q_Learn.py to be your own file, and change the TOH_MDP.py file to import the renamed file (as well as your custom Value Iteration file).
Implement Q-learning to work in two contexts. In one context,
a user can "drive" the agent through the problem space by selecting
actions through the GUI. After each action is executed by the system,
your
In the second context, your function In order control the compromise, you should implement epsilon-greedy Q-learning. You should provide two alternatives: (a) fixed epsilon, with the value specified by the GUI or the system (including possible autograder), and (b) custom epsilon-greedy learning. In the latter, your program can set an epsilon value and change it during the session, in order to gradually have the agent focus more on exploitation and less on exploration. You are encouraged to develop another means of controlling the exploitation/exploration tradeoff. Implementing the use of an exploration function is optional and worth 5 points of extra credit. The GUI provides a means to control whether you are using it or not. However, it is up to you to handle it when it is selected. One unusual feature of some of the MDPs that we use in studying AI is goal states (or "exit states") and exit actions. In order to make your code consistent with the way we describe these in lecture, adhere to the following rules when implementing the code that chooses an action to return:
if is_valid_goal_state(s):
print("It's a goal state; return the Exit action.")
elif s==Terminal_state:
print("It's not a goal state. But if it's the special Terminal state, return None.")
else:
print("it's neither a goal nor the Terminal state, so return some ordinary action.")
Here is the starter code for this assignment.
|
| What to Turn In.
For Part A, Turn in your Value Iteration Python file, named with the scheme YourUWNetID_VI.py. Also, turn in your slightly modified version of TOH_MDP.py, without changing its name. (The modification this time is that it imports your Value Iterations file. You can leave the import of YourUWNetID_Q_Learn as it is in the starter code for this first submission.) ). Finally, be sure to turn in your report file, named using the pattern YourUWNetID_A6_Report.pdf. For the optional Part B, turn your Q_Learn Python file, named with
the scheme YourUWNetID_Q_Learn, and a version of TOH_MDP.py that
imports both of your custom modules (your Value Iteration module
and your Q_Learn module.)
Do not turn in any of the other starter code files (Vis_TOH_MDP.py, TowersOfHanoi.py, or the actual "YourUWNetID_VI.py" or "YourUWNetID_Q_Learn.py"). |
| Footnotes and Implementation Notes:
*The "golden path" is the shortest path from the initial state to the goal state (the state with all disks on the third peg). You can see the golden path using the starter-code GUI (running TOH_MDP.py from within IDLE), by selecting the MDP Rewards menu and then selecting "show golden path". The "silver path" is the shortest path from the initial state to the special state where the top n-1 disks have been moved to peg 3, but the largest disk remains on peg 1. (The code does not offer a display of the silver path.) Note that actions are represented in the actions list as strings. You should not need to ever apply actions in your code, because all states for this MDP have already been generated in advance. When you need to get a T(s, a, sp) value, you come up with the three arguments and call the T function directly. The sp states that are relevant to a particular state s can be obtained from STATES_AND_EDGES[s], which is precomputed in the TOH_MDP starter code. |
| Updates and Corrections:
If necessary, updates and corrections will be posted here and/or mentioned in class or on Piazza.
|
