CSE 410 22wi Homework 5
Compiling / Pipelining / Parallelism

Out: Thursday, 10 February
Due: Wednesday, 16 February, 11:59 pm
Latest Possible Submission Time: Saturday, 19 February, 11:59pm
Turnin: Gradescope

Overview

All parts of this question are about code the compiler produces for this bit of C (whose meaning should be clear to you because it's the same as in Java). Both the scalar (integer) variable i and the integer array A are local variables. 

    for (i=1; i<100; i++) {
       A[i] += A[i-1];
    }

Part I - Pipelining

These four questions show four versions of the assembler produced by the compiler when asking it to perform differing levels of optimization. (Low optimization allows it to compiler faster but produces code that runs slower, higher optimization is the opposite.) For each our goal is to determine how efficiently a pipeline that performs forwarding can execute the sequence of intructions. If forwarding works perfectly, the pipeline can issue (and so complete) one instruction per cycle (once the pipeline is full). When forwarding fails, a bubble will need to be inserted, and so it will take more than K cycles to issue K instructions from the program because the hardware will need to add the bubble(s).

For each snippet of assembler shown, corresponding to different optimization levels, indicate how many cycles are needed to issue all the instructions on a 5 stage pipeline with forwarding. The differences among the number of cycles reflect both the limitations of pipelining and the distinctions in the code that might be produced by the compiler.

Question 1 - Pipelined Execution of Unoptimized Code (-O0)

.L3:
    lw      a5,-20(s0)
    slli    a5,a5,2
    addi    a4,s0,-16
    add     a5,a4,a5
    lw      a4,-404(a5)
    lw      a5,-20(s0)
    addi    a5,a5,-1
    slli    a5,a5,2
    addi    a3,s0,-16
    add     a5,a3,a5
    lw      a5,-404(a5)
    add     a4,a4,a5
    lw      a5,-20(s0)
    slli    a5,a5,2
    addi    a3,s0,-16
    add     a5,a3,a5
    sw      a4,-404(a5)
    lw      a5,-20(s0)
    addi    a5,a5,1
    sw      a5,-20(s0)
.L2:
    lw      a4,-20(s0)
    li      a5,99
    ble     a4,a5,.L3

How many cycles are required to issue all the instructions in this version of the code?

It takes one cycle to issue each instruction plus one cycle for each bubble that has to be inserted because of RAW dependences on values produced by a lw instruction (as that dependence cannot be resolved by forwarding). THere are 23 instructions and 5 unresolvable RAW dependences, so it takes 28 cycles to issue these instructions.

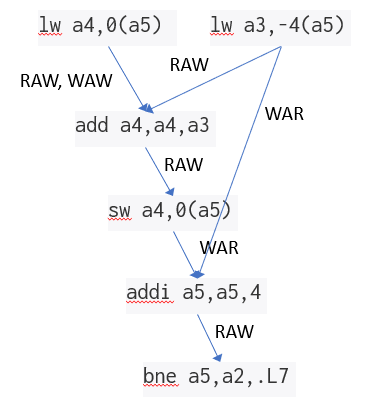
Question 2 - Pipelined Execution of Slightly Optimized Code (-O1)

In this version the compiler doesn't bother to update local variable i as it goes through the loop. Instead, it recognizes that it can have a register pointing at the next array element and just increment that pointer by 4 each iteration. (a5 is that pointer. a2 is a pointer to the end of array. Both are initialized before entering the loop.) 

.L7:
    lw      a4,0(a5)
    lw      a3,-4(a5)
    add     a4,a4,a3
    sw      a4,0(a5)
    addi    a5,a5,4
    bne     a5,a2,.L7

How many cycles are required to issue all the instructions in this version of the code?

There are 6 instructions and one unresolvable RAW dependence, so 7 cycles.

Question 3 - Pipelined Execution of Optimized Code (-O2)

We ask the compiler to try harder to optimize. 

.L4:
     lw      a4,0(a5)
     lw      a3,-4(a5)
     addi    a5,a5,4
     add     a4,a4,a3
     sw      a4,-4(a5)
     bne     a5,a2,.L4

(A) How many cycles are required to issue all the instructions in this version of the code?

There are 6 instructions and no unresolvable RAW dependence, so 6 cycles.

(B) What optimization did the compiler make here, relative to the -O1 case?

The compiler moved the addi instruction to immediately after the lw, thus allowing the pipeline to issue a useful instruction instead of being forced to issue a bubble. This was possible because the addi has no dependences with any of the instructions it "passed" when moving it earlier in the execution sequence.

Question 4 - Pipelined Execution of Highly Optimized Code (-O3)

      .L4:
      lw      a3,0(a5)
      addi    a5,a5,4
      add     a4,a4,a3
      sw      a4,-4(a5)
      bne     a5,a2,.L4

(A) How many cycles are required to issue all the instructions in this version of the code?

There are 5 instructions and no unresolvable RAW dependence, so 5 cycles.

(B)The compiler optimized across loop iterations by recognizing that the value stored at the end of an iteration (in the previous verison of the code) was loaded at the top of the next iteration. It found a way to avoid the re-load. (It must still store a value each iteration because of the meaning of the C loop.)

Part II - General Parallel Execution of Instructions

Question 5 - Parallel Execution of Slightly Optimized Code (-O1)

(A) Draw a dependence diagram of the instruction stream from Question 2 (-O1). Label each dependence with its type: RAW (read-after-write), WAR (write-after-read), or WAW (write-after-write).

(B) Assuming that the CPU has enough hardware resources (e.g., ALU's) that instructions are never delayed due to hardware contention but only due to dependences, and assuming that each instruction can be completed in one cycle once it is eligible to run, how lmany cycles would such a processor take to execute the instruction sequence?

5 cycles

Turnin

Turnin a pdf file with your answers on Canvas.