CSE390D Notes for Friday, 11/22/24
Let R be a relation from A to B
S be a relation from B to C
The composite of R and S, S o R, is the relation from A to C:
S o R = {(a, c) | exists b such that (a, b) in R and (b, c) in S}
Examples:
Parent = {(a, b) | a is a parent of b}
Sister = {(a, b) | a is a sister of b}
Brother = {(a, b) | a is a brother of b}
what are:
Parent o Parent?
(a, c) with a parent of b and b parent of c
grandparent
Sister o Parent?
(a, c) with a parent of b and b sister of c
sister's parent
Powers of a Relation
R^1 = R
R^(n+1) = R^n o R
example: R = facebook friends
R^2 = friend of a friend
R^3 = friend of a friend of a friend
6 degrees of separation
Leskovic found average 6.6 IM links (30B messages, 240M people)
R is transitive iff (R^n subset of R) for all n in Z+
----------------------------------------------------------------------
used one primary example of a relation:
R = {(1, 2), (2, 3), (3, 1), (3, 5), (4, 5), (5, 4)}
digraph version of R can be gotten from GraphViz (relation.dot):
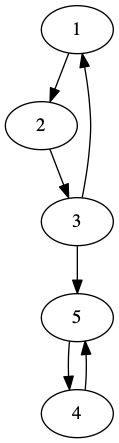 Here is the file contents:
digraph {
1 -> 2
2 -> 3
3 -> 1
3 -> 5
4 -> 5
5 -> 4
}
Then asked them for R^2 as set and as a digraph.
R^2 = {(1, 3), (2, 1), (2, 5), (3, 2), (3, 4), (4, 4), (5, 5)}
Here is the file contents:
digraph {
1 -> 2
2 -> 3
3 -> 1
3 -> 5
4 -> 5
5 -> 4
}
Then asked them for R^2 as set and as a digraph.
R^2 = {(1, 3), (2, 1), (2, 5), (3, 2), (3, 4), (4, 4), (5, 5)}
 Talked about what it means in the digraph for something to be
reflexive, symmetric, antisymmetric.
Then showed matrix representation of R.
0 1 0 0 0
0 0 1 0 0
1 0 0 0 1
0 0 0 0 1
0 0 0 1 0
Then ask them for matrix of R^2...as an example, how to compute element (3, 2)?
Want (3, x) and (x, 2) from R for x=1,2,3,4,5
So that's row 3 for (3, x) and column 2 for (x, 2)
mention idea of matrix multiplication
we don't do a lot with it in 390d because they take linear algebra but
intuitions are important
----------------------------------------------------------------------
switched to sheets to show them R
talked about what it means in matrix form for relation be reflexive,
symmetric, antisymmetric.
showed them R^2 computed with mmult.
talked about reflexive closure, symmetric closure.
symmetric closure = R U R^-1
used mmult to show them R^2, R^3, R^4, R^5
talked about these as paths
How do you get transitive closure?
U of R's
need more than 5? no (in general, need n)
Talked about what it means in the digraph for something to be
reflexive, symmetric, antisymmetric.
Then showed matrix representation of R.
0 1 0 0 0
0 0 1 0 0
1 0 0 0 1
0 0 0 0 1
0 0 0 1 0
Then ask them for matrix of R^2...as an example, how to compute element (3, 2)?
Want (3, x) and (x, 2) from R for x=1,2,3,4,5
So that's row 3 for (3, x) and column 2 for (x, 2)
mention idea of matrix multiplication
we don't do a lot with it in 390d because they take linear algebra but
intuitions are important
----------------------------------------------------------------------
switched to sheets to show them R
talked about what it means in matrix form for relation be reflexive,
symmetric, antisymmetric.
showed them R^2 computed with mmult.
talked about reflexive closure, symmetric closure.
symmetric closure = R U R^-1
used mmult to show them R^2, R^3, R^4, R^5
talked about these as paths
How do you get transitive closure?
U of R's
need more than 5? no (in general, need n)
Stuart Reges
Last modified: Fri Nov 22 12:51:15 PST 2024

