Boolean Logic and Functions

You are encouraged to post any questions about the reading on the course discussion board!

Our first step in building a computer is learning about circuits! In order to be able to reason about and build circuits, we need to first learn a little bit about boolean logic.

What is Boolean Logic?

Boolean logic is a definition built around two boolean values: true and false. You’ve actually used these boolean values in Java before! It turns out that having a formal way to reason about these values is super useful when building hardware, and defining this reasoning is our first step towards building a computer.

Why Two Values? An Important Abstraction

It turns out that the signals on the physical wires in our computer hardware could have any number of volts from 0 - 5 continuously. For our purposes, we are going to choose an abstraction that only has 2 values: a “high” signal (near 5 volts) or a “low” signal (near 0 volts). You might be wondering, why limit ourselves to only two values, high and low? In reality most hardware is designed to have an abstraction of just two values of voltage. This significantly reduces errors in hardware, and ends up being easier to reason about (by allowing us to use boolean logic).

As we noted above, boolean logic traditionally has only two values as well: true and false. We can then map our two-value voltage system to these two values - “high” signals correspond to true, and “low” signals correspond to false. Additionally, often the binary digits 1 and 0 are used to refer to values in this system, with 1 being a high signal/true value, and 0 being a low signal/false value. Lots of different ways of referring to the same thing!

This is the first of many powerful abstractions we will come across when building a computer - our discrete 2-value system allows us to not worry about the actual voltage reading when interpreting a wire’s value.

Boolean Algebra

Boolean algebra is a set of operations for combining boolean values. Just like the algebra you’ve learned in school has operations to combine decimal values (e.g. 3 + 5 = 8) boolean algebra defines a set of operations for combining boolean values. A boolean operation is specified by something called a truth table. A truth table enumerates every possible combination of inputs for that boolean operation, and then specifies what the output should be for each input combination. Three common boolean operations are:

x And y - outputs true (1) only if both x and y are true. Truth Table:

x y out
0 0 0
0 1 0
1 0 0
1 1 1

x Or y - outputs true (1) only if at least one of x or y are true. Truth Table:
x y out
0 0 0
0 1 1
1 0 1
1 1 1

Not x - Outputs true (1) if x is false (0) and false if x is true. Truth table (note how we only have 2 rows now because there are only 2 possible values for a single input):
x out
0 1
1 0

Note that you can define a boolean operation both by a written description and by using a truth table. The latter is a much more explicit way of defining a function - it tells you exactly what that function does for every possible output combination.

Boolean expressions are combinations of boolean operators that evaluate to a value. We can evaluate a boolean expression by applying the truth table over and over until we are left with a single value.

Example: Not(0 Or (1 And 1)) = Not (0 or 1) = Not (1) = 0

Boolean Functions

We can also define our own boolean functions! All we need to do is give names to the inputs for our function, and then specify what the outputs are for those inputs. This can be specified as either a truth table or as a boolean expression of our inputs!

For example we could specify a function as: f(x, y, z) = (x And y) Or (Not(x) And z)

Now someone can figure out the output for a combination of inputs by plugging the input values into our boolean expression. We can also use this boolean expression to build up a truth table for our boolean function. All we need to do is evaluate our boolean expression for each row of our truth table.

For example, the second row in the below truth table is evaluated as follows: 

f(0, 0, 1) = (0 And 0) Or ((Not 0) And 1)
           = 0 Or ((Not 0) And 1)
           = 0 Or (1 And 1)
           = 0 Or 1
           = 1

See if you can fill out the remaining rows in our truth table (full truth table is given in the “Exercise Solutions” section at the bottom of this reading).
f(x, y, z) = (x And y) Or (Not(x) And z)

x y z out
0 0 0
0 0 1 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

Boolean Logic, Hardware, and Circuit Diagrams

Why are we learning about boolean functions? It turns out that computer circuits can be represented by boolean functions! Values (such as 0 and 1) are carried on wires, operators (such as And) map to physical circuit gates, and combinations of wires and physical circuit gates build our hardware devices. When we say x And y, we are describing a physical circuit, with a wire corresponding to the x input, a wire corresponding to the y input, and an And gate connecting the two input wires and sending an output signal on another wire. This is the basis of our work for the first few weeks of this class.

Circuit diagrams are another way of representing boolean logic and are often used when designing hardware. They make use of conventional symbols to represent logic gates (see Chapter 1 of the textbook for more of these symbols).

Example: a Or b

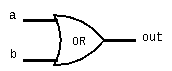
We can also combine operations by wiring logic gates together.

Example: Not((a Or b) And c)

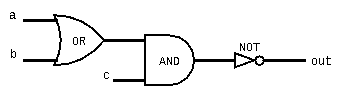
Simplifying Boolean Functions

Simplifying boolean functions is actually a top priority when designing hardware. Simpler boolean functions require less wires and gates to implement which ultimately lead to cheaper and faster hardware. One way of simplifying boolean functions is by applying boolean identities to a boolean function. These identities define equivalent boolean expressions that allow us to manipulate our boolean functions and potentially create simpler expressions. A non-exhaustive list is:

Let’s say we have the function f(x, y) = Not(Not(x) And Not(y)). We can apply identities to potentially simplify that function: 

Not(Not(x) And Not(y)) **use De Morgan’s Law**
= Not(Not(x)) Or Not(Not(y)) **use double negation**
= x Or y

Another way of simplifying our expression is to build up a truth table for it and see if it matches any functions we know already.
f(x, y) = Not(Not(x) And Not(y))

x y out
0 0 0
0 1 1
1 0 1
1 1 1

That looks exactly like the truth table for x Or y! We won’t ask you to do too much simplifying in this course, but it is an important part of hardware design so we thought it would be worth mentioning.

Boolean Function Synthesis

We’ve talked about creating a truth table from an existing boolean expression, now let’s talk about creating a boolean expression from an existing truth table! This is an important part of hardware design - often we will know the outputs we want for each set of inputs (i.e. we know the truth table), and then we have to create a boolean expression so that we can define the logic gates for our function and ultimately build the hardware corresponding to it. Suppose we have the following truth table for our function:

x y z out
0 0 0 1
0 0 1 0
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 0
1 1 1 0

Our plan is going to be this: first, for each row where the output is "true", define a function that is "true" for that row and only that one row. Then, since we have expressions for each of the true rows, we can combine them together to get an expression for the entire truth table.

It turns out we can describe any row in terms of And and Not gates. For each input, if a 1 appears in the row, we will use just the input, and if a 0 appears we will negate the input. Then we can combine our inputs with And gates.
For example: row1(x, y, z) = Not(x) And Not(y) And Not(z)

We can see that row1 is only true for the first row in our truth table!

x y z out row1
0 0 0 1 1
0 0 1 0 0
0 1 0 1 0
0 1 1 0 0
1 0 0 1 0
1 0 1 0 0
1 1 0 0 0
1 1 1 0 0

Let’s do the same for the other "true" rows:
row3 = Not(x) And y And Not(z)
row5 = x And Not(y) And Not(z)

x y z out row1 row3 row5
0 0 0 1 1 0 0
0 0 1 0 0 0 0
0 1 0 1 0 1 0
0 1 1 0 0 0 0
1 0 0 1 0 0 1
1 0 1 0 0 0 0
1 1 0 0 0 0 0
1 1 1 0 0 0 0

Now we just need to combine our different row expressions to get our final expression (we'll name our function f). Note that to get f, we want a 1 to appear in a row if there is at least one 1 in one of the other rows. What operation does “at least” remind you of? Yup, an Or operation! We combine our row expressions using Or to get our final expression for f.
f(x, y, z) = row1 Or row2 Or row3
f(x, y, z) = (Not(x) And Not(y) And Not(z)) Or (Not(x) And y And Not(z)) Or (x And Not(y) And Not(z))

That is a totally correct boolean expression! We can simplify that expression if we want to (it is pretty long...), but I think it’s important to point out that the expression above correctly describes the truth table we started with; it’s just maybe a little more verbose than we would like it to be. From here we can simplify using boolean identities (omitting the steps because it is not the focus of this section), resulting in the final expression:
f(x, y, z) = Not(z) And (Not(x) Or Not(y))

It’s pretty neat that this process works for every possible truth table/boolean expression out there! To summarize the process, to get a boolean expression for a given truth table we:

  1. Create an expression for each “true” row in the truth table using And and Not.
  2. Combine these individual expressions with Or.
  3. Now we have a completely correct expression for the truth table! We can simplify further if we’d like to (often hardware designers will want to do this).

The Road Ahead

Hopefully this was an interesting look into the world of boolean logic! In lecture, we will continue to explore the connection between boolean logic and hardware design, with the goal of getting you setup to start designing your own hardware gates on project 1.

Exercise Solution

Full truth table for f(x, y, z) = (x And y) Or (Not(x) And z)

x y z out
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 1