Reading 2: Boolean Logic and Functions
Our first step in building a computer is learning about circuits. In order to be able to reason about and build circuits, we need to first learn about the concept of Boolean logic.
What is Boolean Logic?
Boolean logic is a definition built around two Boolean values: True and false. You’ve used these Boolean values in Java before. It turns out that having a formal way to reason about these values is useful when building hardware, and defining this reasoning is our first step towards building a computer.
Why Two Values? An Important Abstraction
It turns out that the signals on the physical wires in our computer hardware could have any number of volts from 0-5 continuously. For our purposes, we are going to choose an abstraction that only has two values: A “high” signal (near 5 volts) or a “low” signal (near 0 volts). You might be wondering, why limit ourselves to only two values, high and low? In reality, most hardware is designed to have an abstraction of just two values of voltage. This significantly reduces errors in hardware and ends up being easier to reason about (by allowing us to use Boolean logic).
As noted above, Boolean logic traditionally has only two values as well: True and false. We can then map our two-value voltage system to these two values: “High” signals corresponding to true and “low” signals corresponding to false. Oftentimes, the binary digits 0 and 1 are used to refer to values in this system, with 0 being false or a low voltage signal and 1 being true or a high voltage signal. As we can see here, there are many different ways to refer to the same thing.
This is the first of many powerful abstractions we will come across when building a computer - our discrete 2-value system allows us to not worry about the actual voltage reading when interpreting a wire’s value.
Boolean Algebra
Boolean algebra is a set of operations for combining Boolean values. Just like how the algebra we've learned in high school involves operations to combine decimal values (e.g., 3 + 5 = 8), Boolean algebra defines a set of operations for combining Boolean values. A Boolean operation is specified by a truth table. A truth table enumerates every possible combination of inputs for that Boolean operation, and then specifies what the output should be for each input combination. Here are three examples of Boolean operations with their corresponding truth tables:
x And y outputs 1 only if both x and y are both true and 0 otherwise.
x |
y |
out |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
x Or y outputs 1 only if at least one of x or y are true and 0 otherwise.
x |
y |
out |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Not x Outputs 1 if x is 0 and 0 if x is 1. Notice how we only have two rows now because there are only two possible values for a single input.
x |
out |
| 0 | 1 |
| 1 | 0 |
You can define a Boolean operation both by a written description and by using a truth table. The latter is a much more explicit way of defining a function, informing you exactly what that function does for every possible output combination.
Boolean expressions are combinations of Boolean operators that evaluate to a value. We can evaluate a Boolean expression by evaluating simpler Boolean algebra expressions using the appropriate truth tables until we are left with a result of 0 or 1.
Example: Not(0 Or (1 And 1)) = Not(0 or 1) = Not(1) = 0
Boolean Functions
We can also define our own Boolean functions. All we need to do is give names to the inputs for our function, and then specify what the outputs are for those inputs. This can be specified as either a truth table or as a Boolean expression of our inputs.
For example, we could specify a function as: f(x, y, z) = (x And y) Or (Not(x) And z)
We can determine the output for a combination of inputs by plugging the input values into a Boolean expression. We can also use this Boolean expression to build up a truth table for our Boolean function. All we need to do is evaluate our Boolean expression for each row of our truth table.
For example, the second row in the below truth table is evaluated as follows:
f(0, 0, 1) = (0 And 0) Or ((Not 0) And 1)
= 0 Or ((Not 0) And 1)
= 0 Or (1 And 1)
= 0 Or 1
= 1
Exercise: Fill out the remaining rows in our truth table (full truth table is given in the “Exercise Solutions” section at the bottom of this reading).
f(x, y, z) = (x And y) Or (Not(x) And z)
x |
y |
z |
out |
| 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 |
Notice the way we have defined the inputs of the truth table. In the first column, the first half of the rows are 0s and the latter half of the rows are 1s. In the second column, the first quarter of the rows are 0s and the second quarter of the rows are 1s, and so on. As we will later learn, defining the inputs this way is convenient, as the binary values of each row from the top row to bottom row are in increasing order.
Boolean Logic, Hardware, and Circuit Diagrams
Why are we learning about Boolean functions? It turns out that computer circuits can be represented by Boolean functions. Values (such as 0 and 1) are carried on wires, operators (such as And) map to physical circuit gates, and combinations of wires and physical circuit gates build our hardware devices. When we say x And y, we are describing a physical circuit, with a wire corresponding to the x input, a wire corresponding to the y input, and an And gate connecting the two input wires and sending an output signal on another wire. This is the basis of our work for the first few weeks of this class.
Circuit diagrams are another way of representing Boolean logic and are often used when designing hardware. They make use of conventional symbols to represent logic gates (see Chapter 1 of the textbook for more of these symbols).
Example: a Or b
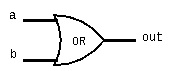
We can also combine operations by wiring logic gates together.
Example: Not((a Or b) And c)
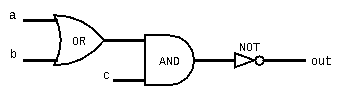
Simplifying Boolean Functions
Simplifying Boolean functions is actually a top priority when designing hardware. Simpler Boolean functions require fewer wires and gates to implement which ultimately lead to cheaper and faster hardware. One way of simplifying Boolean functions is by applying Boolean identities to a Boolean function. These identities define equivalent Boolean expressions that allow us to manipulate our Boolean functions and potentially create simpler expressions. Here is a nonexhaustive list of Boolean identities:
- Commutativity
(x And y) = (y And x)(x Or y) = (y Or x)
- Associativity
(x And (y And z)) = ((x And y) And z)(x Or (y Or z)) = ((x Or y) Or z)
- Distributive Property
(x And (y Or z)) = (x And y) Or (x And z)(x Or (y And z)) = (x Or y) And (x Or z)
- De Morgan's Law
Not(x And y) = Not(x) Or Not(y)Not(x Or y) = Not(x) And Not(y)
- Double Negation
Not(Not(x)) = x
Let’s say we have the function f(x, y) = Not(Not(x) And Not(y)). We can apply identities to simplify this function:
Not(Not(x) And Not(y)) = Not(Not(x)) Or Not(Not(y)) [De Morgan’s Law]
= x Or y [Double negation]
Another way of simplifying our expression is to build up a truth table for it and see if it matches any functions we know already. Consider the following function and its corresponding truth table:
f(x, y) = Not(Not(x) And Not(y))
x |
y |
out |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
This looks exactly like the truth table for x Or y! We won’t ask you to worry about simplifying in this course, but we want to emphasize that it's an important part of hardware design.
Boolean Function Synthesis
We’ve talked about creating a truth table from an existing Boolean expression. Now, let’s talk about creating a Boolean expression from an existing truth table. This is an important part of hardware design—often, we will know the outputs we want for each set of inputs (i.e., we know the truth table), and then we have to create a Boolean expression so that we can define the logic gates for our function and ultimately build the hardware corresponding to it. Suppose we have the following truth table for our function:
x |
y |
z |
out |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Here is our plan of attack to create a Boolean expression from a truth table. First, for each row where the output is 1, we define a function that is 1 for that row and only that one row. Now, we have a Boolean expressions for each of the rows that evaluate to true, so we can combine them together to get an expression for the entire truth table.
It turns out we can describe any row in terms of And and Not gates. For each input of a given row, if a 1 appears in the row, we will use just the input itself. On the other hand, if a 0 appears, we will negate the input using a Not gate. Then, we can combine our inputs with And gates.
For example: row1(x, y, z) = Not(x) And Not(y) And Not(z)
We can see that row1 is only true for the first row in our truth table.
x |
y |
z |
out |
row1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Let’s do the same for the other rows that evaluate to 1:
row3 = Not(x) And y And Not(z)
row5 = x And Not(y) And Not(z)
x |
y |
z |
out |
row1 |
row3 |
row5 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Now, we just need to combine our different row expressions to get our final expression (we'll name our function f). Note that to get f, we want the output of f to be 1 if at least one of the rows evaluates to a 1. What operation does “at least” remind you of? That's right, an Or gate. We combine our row expressions using Or to get our final expression for f:
f(x, y, z) = row1 Or row3 Or row5
f(x, y, z) = (Not(x) And Not(y) And Not(z)) Or (Not(x) And y And Not(z)) Or (x And Not(y) And Not(z))
While unsimplified, this Boolean expression that we've arrived at is correct. We can simplify that expression if we wanted to, but the key takeaway here is that this expression is valid. Here is the simplified expression (omitting the steps because they're unimportant in this context):
f(x, y, z) = Not(z) And (Not(x) Or Not(y))
The Boolean function synthesis strategy works for every possible truth table out there. To summarize the process, we can get a Boolean expression for a given truth table by:
- Create a Boolean expression for each row that has an output of
1in the truth table usingAndandNot. - Combine these individual expressions with
Or. - Now, we have a completely correct expression for the truth table. We can simplify further if we’d like to.
The Road Ahead
In lecture, we will continue to explore the connection between Boolean logic and hardware design, with the goal of getting you setup to start designing your own hardware gates on Project 1.
Exercise Solution
Full truth table for f(x, y, z) = (x And y) Or (Not(x) And z)
x |
y |
z |
out |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |