Program Specification

Synopsis¶

For HW8, you will be writing a small C++ library to represent and manipulate equations with variables. Although we can already write math expressions in C++, we cannot directly express an equation with variables like x or m. For example, if we want to represent the equation y = mx + b, we could create a function that takes x, m, and b, but this is time consuming and inflexible.

Instead, we are creating a base class called Expr which represents a math expression, which may or may not contain variables. Examples of expressions include m*x+b, 42+374, x, etc.

Expr is the base class which is extended via inheritance to be a number (Num), variable (Var), or a sum of two other Expr’s (Sum). You will also add a multiplication expression (Prod) and an exponential expression (Pow).

For example, the expression m*x+b would be represented as a Sum of two other Expr‘s. The first Expr is a Prod of two Vars m and x, the second just a single Var b.

To make this library convenient to use, we will be overloading the standard C++ operators for multiplication and addition, as well as using the ^ operator to represent exponentiation, so that you can write Expr expressions as C++ code.

This data structure is a form of an “Abstract Syntax Tree” (AST): the AST specifies the structure of the math notation we write. For example, the expression m*x + b requires knowledge of order-of-operations to recognize that the multiplication is performed before the addition; the AST explicitly represents this relationship as a tree. We will be taking advantage of C++’s standard operator precedence rules to construct the correct AST for the expression we write.

As an example, consider the expression x+2*y^3+5. In AST form, it looks like this:

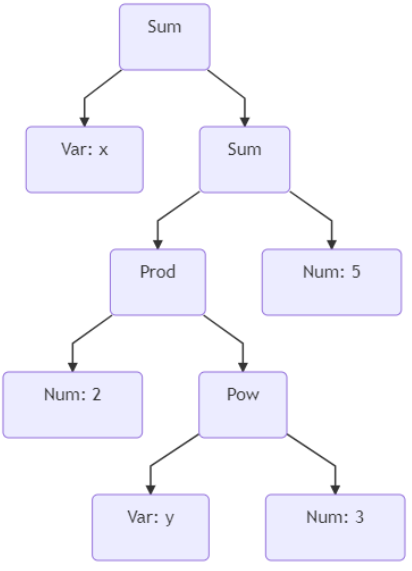
Part 1: setVariables() for Num, Sum, Var¶

If you run make right now, it should print a warning about not returning anything in setVariables(), but it will generate the ./main executable. If you run ./main it will segfault. We need to implement the setVariables() function for Num, Sum, and Var.

This is a recursive function which will replace some or all of the Var nodes with Num nodes, based on the map from variable names to double values. In other words, it is used to create a new expression that replaces the variables with the corresponding numerical values, if those exist in the map. It should not perform any numerical computations. The goal of this function is to ultimately return an actual number.

For example, in main.cc they call exp1->setVariables(values), which should return an expression with all the “x” variables replaced with 42 and all the “y” variables replaced with “43”.

setVariables() has two base cases: Num and Var.

• The implementation for Num is the simplest, it should just return a copy of itself, and wrapped it with a shared_ptr.
• Var should check if its own variable name is in the map passed in. If it is not, then just return a copy of itself, and wrapped it with a shared_ptr. If its own variable name is in the map, it should return a wrapped Num object owned by a shared_ptr where the number is the value associated with its variable name.
• Sum is the recursive case; just call setVariables() on the left and right expression.

After doing this, you should be able to recompile and not get a segmentation fault when running ./main.

Part 2: Prod and operator*()¶

Now, implement a Prod node representing multiplication (product). You should see the class in Expr.h. This process should be pretty similar to implementing Sum since they are both operators which have two expressions.

You will have to add the functions to Expr.cc:

• Prod::Prod(shared_ptr<Expr> left, shared_ptr<Expr> right)
• shared_ptr<Expr> Prod::clone() const
• shared_ptr<Expr> Prod::setVariables(const std::map<std::string, double>& values) const
• shared_ptr<Expr> operator*(shared_ptr<Expr> lhs, shared_ptr<Expr> rhs)
• double Prod::evaluate() const

For operator*(shared_ptr<Expr> lhs, shared_ptr<Expr> rhs), check out the operator+(shared_ptr<Expr> lhs, shared_ptr<Expr> rhs) implementation provided in Expr.cc.

After doing this you should be able to uncomment the next block of code in main.cc. When you run make it should compile ./main. Running ./main, you should see the actual output match the expected output.

Part 3: Pow and operator^()¶

Now, implement a Pow node representing an exponent (e.g. x^2). The Pow class is in Expr.h, but it doesn’t have any of the methods or data members in it, so fill those in. It should be very similar to Sum and Prod.

Implement each of those functions as well as operator^().

You should now be able to uncomment all of main.cc. Run make and ./main to ensure that it matches the expected output.

Part 4: plot.cc¶

Before working on the plot part of this homework there are two commands you need to run just once to get the Python3 script we have provided to work:

pip3 install --user matplotlib
pip3 install --user numpy

If you run make plot, it should compile plot.cc into plot_csv, then it will run ./plot_csv and the provided ./plot_png.py which will generate line.csv and line.png. The graph should look something like this:

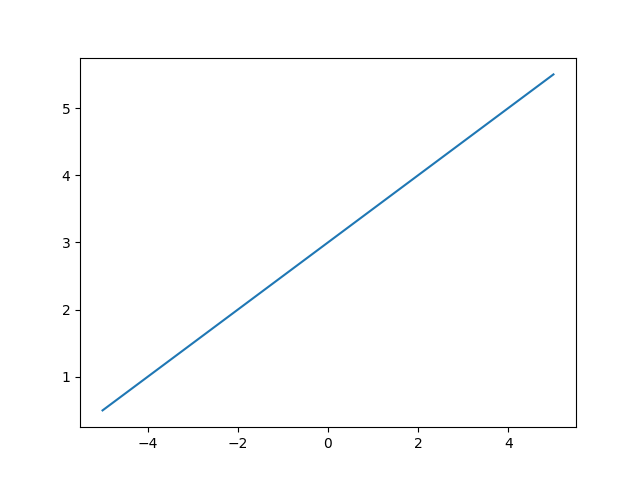
The provided write_file() function plots the y coordinates of an equation, given a set of x points, then writes it into a given filename.

Your job is to use write_file() to plot the y coordinates of a curve equation: 0.5x^2 + 3, writing it into curve.csv.

This should only be a few lines, and the code should look very similar to the line example.