Programming

All of the code for this project is in the cse143review/src folder. Inside, we have two packages: a datastructures package containing a basic linked list and binary tree implementation, and a problems package with a bunch of method stubs and TODOs.

For this project, you will design and implement each of the TODOs listed in the problems package. We also recommend taking a look at the files in the datastructures package as you go through the TODOs to get a better understanding of the data structures used for each problem. As these problems are pulled from the intro series’ course material, you are welcome to use any of your previous code. For this project, this will not be counted as plagiarism.

Array Problems¶

For each of the array problems, you’ll be taking an array as a parameter.

For each of the array problems, do not,

• add any additional imports,
• or create new int[] objects for toString or rotateRight.

toString¶

Implement a method that returns a String representation of the contents of the input int[]. The String representation of the int[] should begin with “[” and end with “]”. Each pair of integers in the String representation should be separated by a comma and a space.

For example, if a variable named array refers to the array:

{5, 10, 15}

Then toString(array) should return the String:

"[5, 10, 15]"

On the other hand if the input array was:

{1}

Then toString(array) should return the String:

"[1]"

reverse¶

Implement a method that returns a new int[] containing the input int[]‘s elements in reverse order. The method should not modify the input array.

For example, if a variable named array refers to an array containing the values:

{1, 2, 3, 4, 5, 6, 7, 8, 9}

The call to reverse(array) should return an array containing the values:

{9, 8, 7, 6, 5, 4, 3, 2, 1}

rotateRight¶

Implement a method that rotates the values in the input int[] to the right (i.e., forward in position) by one. Each element moves right by one, except the last element, which moves to the front.

For example, if a variable named array refers to an array containing the values:

{3, 8, 19, 7}

The call of rotateRight(array) should modify it to store:

{7, 3, 8, 19}

A subsequent call of rotateRight(array) would leave the array as follows:

{19, 7, 3, 8}

Map Problems¶

For each of the Map problems, you’ll be taking a Map as a parameter (even if it doesn’t show up in the method signature).

contains3¶

Implement a method that returns true if any string occurs at least 3 times in the input list, and false otherwise. Use a map as auxiliary storage. For example, consider the following list:

["373", "is", "fun", "HI", "fun", "fun"]

contains3 should return true given this input because “fun” shows up at least 3 times.

intersect¶

Implement a method that takes as input two maps from Strings to Integers and returns a new map whose contents are the intersection of the two. The intersection of two maps is defined here as the set of keys-value pairs that exist in both maps. If some key K maps to value V in both the first and second map, include it in your result. If K does not exist as a key in both maps, or if K does not map to the same value V in both maps, exclude that pair from your result.

For example, consider the following two maps:

map1: {Janet=87, Logan=62, Whitaker=46, Alyssa=100, Stefanie=80, Jeff=88, Kim=52, Sylvia=95}
map2: {Logan=62, Kim=52, Whitaker=52, Jeff=88, Stefanie=80, Brian=60, Lisa=83, Sylvia=87}

Calling intersect(map1, map2) would return the following new map (the order of the key-value pairs does not matter):

{Logan=62, Stefanie=80, Jeff=88, Kim=52}

LinkedIntList problems¶

For each of the LinkedIntList problems, you’ll be taking a list as a parameter and then directly modifying the links between the nodes (the public fields) by using the ListNode class defined in LinkedIntList. You are allowed to have as many ListNode variables as you want (except when told explicitly).

For each of the LinkedIntList problems, do not,

• call any methods on the LinkedIntList objects,
• construct any new ListNode objects for reverse3 or firstToLast,
• use other data structures such as arrays, lists, queues, etc.,
• or mutate the data of any nodes.

reverse3¶

Implement a method to change the following LinkedIntList (you may assume it has these exact 3 elements):

front → 5 → 4 → 3 → /

Into this sequence of ListNode objects:

front → 3 → 4 → 5 → /

This is intended to be a warm-up to the other LinkedIntList problems, so you don’t need to generalize your solution to work for different lists.

firstToLast¶

Implement a method that moves the first element of the input LinkedIntList to the back end of the list.

Suppose a LinkedIntList variable named list stores the following elements from front (left) to back (right):

front → 18 → 4 → 27 → 9 → 54 → 5 → 63 → /

If you call firstToLast(list), the list would then store the elements in this order:

front → 4 → 27 → 9 → 54 → 5 → 63 → 18 → /

If the list is empty or has just one element, its contents should not be modified.

concatenate¶

Implement a method which takes two LinkedIntLists as input and returns a new list containing all the items of the first followed by all the items of the second. Don’t modify the input lists; use the new keyword to create new objects instead. Your implementation should run in linear time i.e. without the use of nested for-loops.

list1: front → 1 → 2 → 3 → /
list2: front → 4 → 5 → 6 → /

If you made the call concatenate(list1, list2), then it should return a new list:

return: front → 1 → 2 → 3 → 4 → 5 → 6 → /

and list1 and list2 would remain unchanged:

list1: front → 1 → 2 → 3 → /
list2: front → 4 → 5 → 6 → /

IntTree Problems¶

For each of the IntTree problems, you’ll be taking a tree as a parameter and then directly modifying the links between the nodes (the public fields) by using the IntTreeNode class defined in IntTree. You are allowed to have as many IntTreeNode variables as you want (except when told explicitly).

For each IntTree problems, do not,

• call any methods on the IntTree objects,
• construct any new IntTreeNode objects,
• use other data structures such as arrays, lists, queues, etc.,
• or mutate the data of any node.

depthSum¶

Implement a method that returns the sum of the values stored in a binary tree of integers weighted by the depth of each value.

You should return the value at the overallRoot, plus 2 times the values stored at the next level of the tree, plus 3 times the values stored at the next level of the tree, and so on. For example, in the tree below:

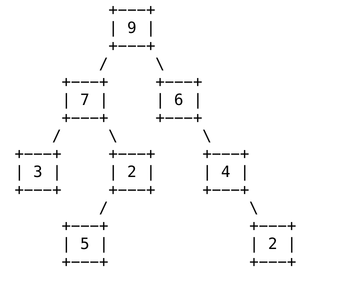
The sum would be computed as:

$$9 + 2 \cdot (7+6) + 3 \cdot (3+2+4) + 4 \cdot (5+2) = 90$$

removeLeaves¶

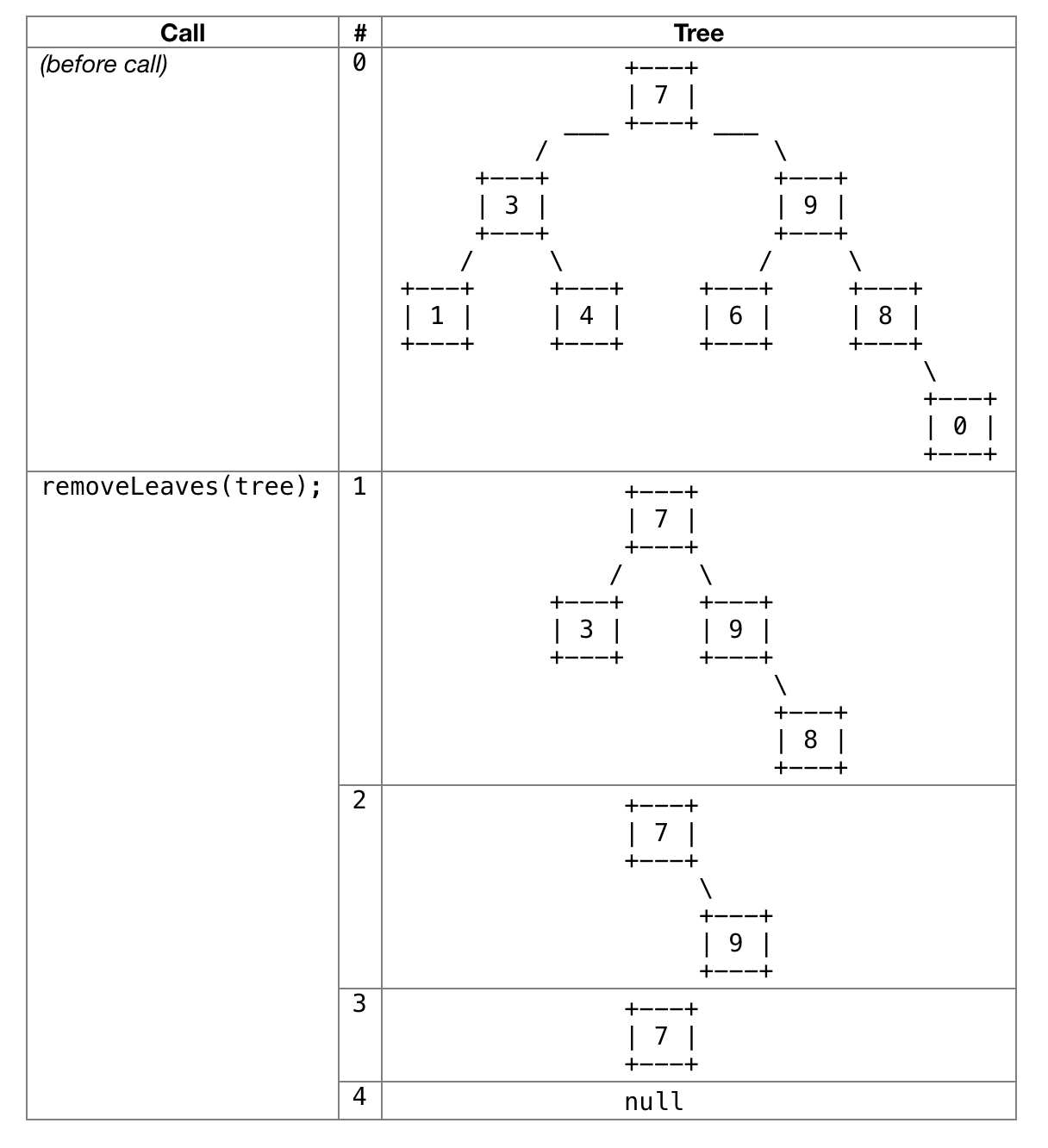
Implement a method that removes the leaf nodes from an IntTree. (Remember that a leaf node is one that has empty left and right subtrees.) If a variable tree refers to the first tree below, the removeLeaves(tree) should remove the four leaves from the tree (the nodes with data values 1, 4, 6, and 0) leaving the next tree below.

A second call on the method would eliminate the two leaves in this tree (the nodes with data values 3 and 8), shown in the third tree below.

A third call would eliminate the one leaf with data value 9, and a fourth call would leave an empty tree because the previous tree was exactly one leaf node.

If your method is called on an empty tree, the method does not change the tree because there are no nodes of any kind (leaf or not).

trim¶

Implement a method that accepts parameters for an IntTree and minimum and maximum integer values, and removes from the tree any elements that are not within that range (inclusive).

For this method, you should assume that your tree is a binary search tree (BST), so its elements are in valid BST order. Your method should maintain the BST ordering property of the tree.

For example, suppose a variable of type IntTree called tree stores the following elements:

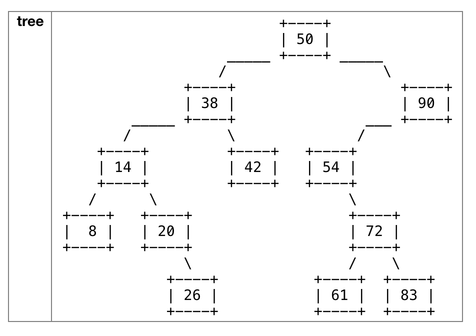
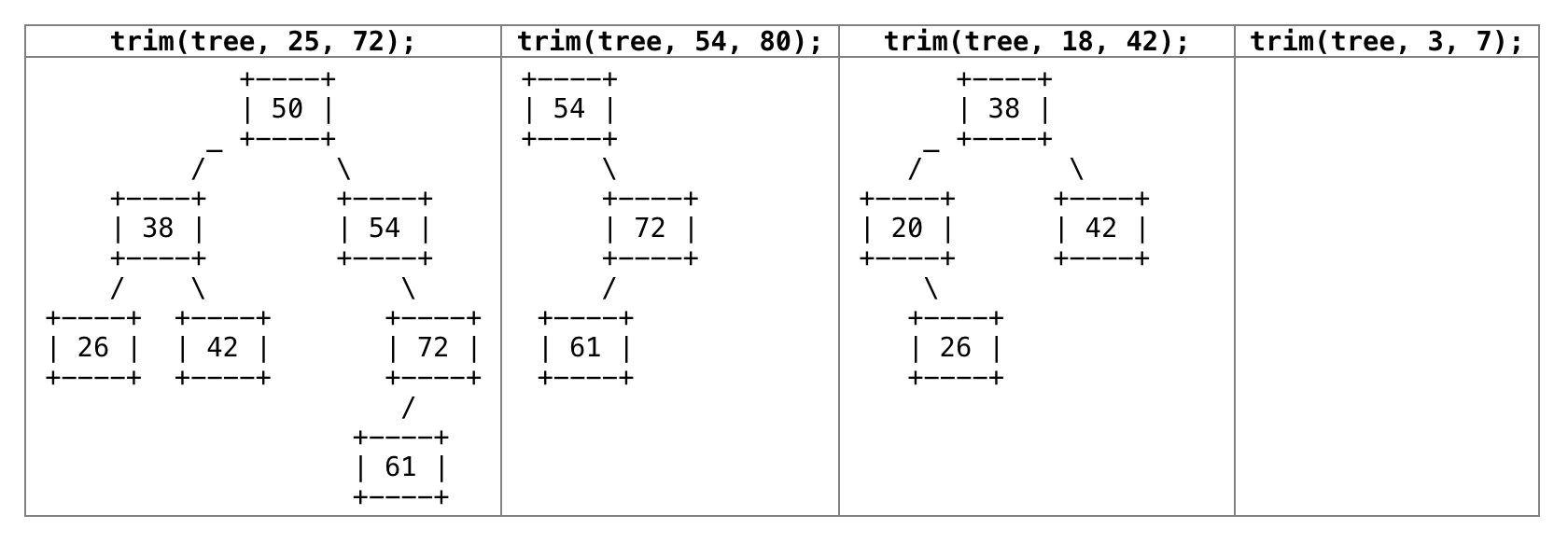
The table below shows what the state of the tree would be if various trim calls were made. The calls shown are separate; they are not a chain of sequential calls. You may assume that the minimum is less than or equal to the maximum.

Hint

The BST ordering property is important for solving this problem. If a node’s data value is too large or too small to fit within the range, this may also tell you something about whether that node’s left or right subtree elements can be within the range. Taking advantage of such information makes it more feasible to remove the correct nodes.

Testing and Submitting¶

For this project, we’ve provided tests inside the cse143review/test module for you to check your work. Run them as you go through each problem. Review the testing page for more info.

Once you have successfully passed all the tests, visit the Commit & Submit page for instructions on saving your work and submitting it for grading.